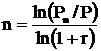Комбинация простого и сложного процентов
В ряде случаев возникает ситуация, когда начисление процентов включает и сложный, и простой проценты. Например, средства вкладчика находятся на счете в банке 5 лет и 2 месяца. Проценты капитализируются (т.е. присоединяются к основной сумме счета, на которую начисляется процент) в конце каждого года. В течение года начисляется простой процент. Для такого случая сумму, которую получит инвестор, можно рассчитать по следующей формуле:
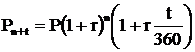
где: Рn+t – сумма, которую получит инвестор за nлет и t дней;
Р– первоначально инвестированная сумма;
t – число дней, за которые начисляется простой процент;
r – процент, начисляемый в течение года.
В зависимости от того, когда вкладчик размещает средства на счете, простой процент может начисляться также в начале периода инвестирования средств или и в начале и в конце. Суммы, которые получит вкладчик, можно рассчитать соответственно с помощью следующих формул (капитализация процентов осуществляется ежегодно):
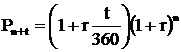
и
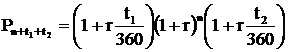
ДИСКОНТИРОВАННАЯ СТОИМОСТЬ
В финансовых расчетах возникает необходимость сравнивать между собой различные суммы денег в разные моменты времени. Например, какая величина больше: 100 тыс. руб. сегодня или 1 млн. руб. через пять лет. Дело в том, что сегодня инвестор может положить 100 тыс. руб. в банк и за пять лет они принесут ему некоторый процент. Если через пять лет 100 тыс. руб. на счете вкладчика превратятся в 1 млн. руб., то можно сказать, что 100 тысяч руб. сегодня и 1 млн. руб. через пять лет – это эквивалентные, т.е. равные во времени суммы. Если вкладчик получит больше 1 млн. руб., тогда 100 тыс. руб. сегодня «стоят» больше 1 млн. руб. через пять лет.
Чтобы сравнить суммы денег во времени, их необходимо привести к единому временному знаменателю. В практике финансовых расчетов принято приводить суммы средств, которые получит инвестор, к сегодняшнему дню, т.е. начальной точке отсчета. Данную задачу решают (при начислении сложного процента) с помощью следующей формулы:
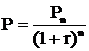
Эта формула называется формулой дисконтированной или приведенной стоимости. Рn – это будущая стоимость, Р – дисконтированная или приведенная стоимость (в литературе в качестве синонимов используют также термины сегодняшняя, настоящая, текущая стоимость).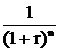 
– это коэффициент дисконтирования.
При начислении сложного процента т раз в год формула принимает вид:
,
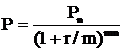а для непрерывно начисляемого процента:
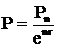
Формулы дисконтированной стоимости для простого процента:
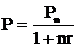
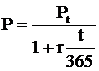
ОПРЕДЕЛЕНИЕ ПЕРИОДА НАЧИСЛЕНИЯ ПРОЦЕНТА
На практике возникают вопросы определения периода времени, которое потребуется для увеличения суммы Р до значения Рn при начислении процента r.
Для простого процента получим:
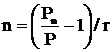
Период t будет равен соответственно:
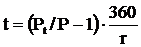
и
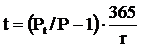
Период времени инвестирования равен:
