Методология финансово-экономических расчетов
Методология финансово-экономических расчетов
Рассмотрим примеры выполнения расчетов для наиболее типичных финансово-экономических расчетов.
Простые проценты
Пример 1.Ссуда в размере 100 000 руб. выдана на срок 1,5 года при ставке простых процентов равной 15% годовых. Определить проценты и сумму накопленного долга при единовременном погашении ссуды по истечении срока.
Известны:
Р = 100 000 руб.,
n =1,5 года,
i = 0,15 или 15% .
Найти
I = ?,S = ?
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств[1].
Для расчета процентов воспользуемся формулой (1)
I = Рni = 100 000 ·1,5 · 0,15 = 22 500 руб.– проценты за пользование ссудой в течение 1,5 лет.
По формуле (2) находим сумму накопленного долга:
S = P (1+ ni )= 100 000 (1+1,5 · 0,15) = 122 500 руб.
Другой способ расчета наращенной суммы, по формуле (3)
S = P + I = 100 000 + 22 500 =122 500 руб.– сумма накопленного долга по истечении 1,5 лет.
2-й вариант.Расчетные формулы и результатывычисления в среде Excel представлены на рис. 1.
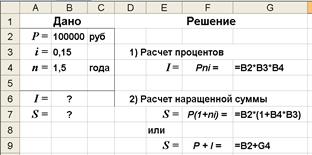
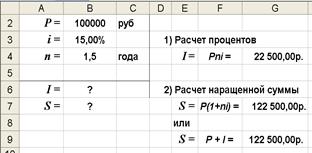
а) б)
Рис. 1. Результаты решения задачи: а) - расчетные формулы,
б) - результаты вычислений
3-й вариант.Вычисления с помощью встроенных функций Excel. Специальная функция для вычисления простых процентов в среде Excel отсутствует.
Практика начисления простых процентов
Ставка процентов обычно устанавливается в расчете за год. При продолжительности ссуды менее года, когда необходимо выяснить, какая часть процента уплачивается кредитору, срок ссуды п выражается в виде дроби:
n = t / K , (4)
где п - срок ссуды (измеренный в долях года),
К - число дней в году (временная база),
t - срок операции (срок пользования ссудой) в днях.
В зависимости от того, какое количество дней в году берется за базу, различают два вида процентов:
- обыкновенный процент (коммерческий), когда в году принимается 360 дней, т.е. 12 месяцев по 30 дней;
- точный процент получают, когда за базу берут действительное число дней в году: 365 или 366.
В зависимости от числа дней пользования ссудой различают два способа начисления процентов:
- точный способ - вычисляется фактическое число дней между двумя датами;
-приближенный способ - продолжительность ссуды определяется числом месяцев и дней ссуды, когда все месяцы содержат по 30 дней.
Следует помнить, что в обоих случаях дата выдачи и дата погашения долга считается за один день.
С учетом этого, на практике могут применяться три варианта расчета процентов:
а) точные проценты с точным числом дней ссуды (английская практика);
б) обыкновенные проценты с точным числом дней ссуды (французская практика);
в) обыкновенные проценты с приближенным числом дней ссуды (германская практика).
Замечание. Вариант расчета с точными процентами и приближенным измерением времени ссуды не применяется.
Пример 2.Ссуда, размером 100 000 руб., выдана на срок с 21 января 2009 г. до 3 марта 2009 г. при ставке простых процентов, равной 15% годовых. Найти:
1) точные проценты с точным числом дней ссуды;
2) обыкновенные проценты с точным числом дней ссуды;
3) обыкновенные проценты с приближенным числом дней ссуды.
Известны:
Р = 100 000 руб.,
Tнач = 21 января 2009 года,
Tкон = 03 марта 2009 года,
i = 0,15 или 15%.
Найти
I1 = ?, I2 = ?,I3 = ?
Решение.
1-й вариант.Для вычисления процентов с помощью подручных вычислительных средств воспользуемся формулой (1) с учетом формулы (4):
I = P n i = P ( t / K ) i.
Предварительно по табл. 1 (Приложение 1), либо по календарю рассчитаем точное число дней между двумя датами: t = 62 - 21 = 41день, тогда получим
1) К= 365, t = 41, I1 = 100 000 * (41 / 365) * 0,15 = 1 684,93 руб.;
2) К= 360, t = 41, I2 = 100 000 * (41 / 360) * 0,15 = 1 708,33 руб.
Приближенное число дней составит 42 дня (январь 9 дней + февраль 30 дней + март 3 дня), тогда начисленные проценты будут равны
3) К= 360, t = 42, I3 = 100 000 * (42 / 360) * 0,15 = 1 750,00 руб.
Следует обратить внимание на то, что для каждого случая получили свой результат.
2-й вариант.Для выполнения расчетов по формулам воспользуемся функцией ДОЛЯГОДА (находится в категории Дата и время). Данная функция возвращает долю года, которую составляет количество дней между двумя датами (начальной и конечной).
Синтаксис функции ДОЛЯГОДА(нач_дата; кон_дата; базис) и ее аргументы:
нач_дата – начальная дата,
кон_дата – конечная дата,
базис – используемый способ вычисления дня. Возможные значения базиса при различных способах вычисления приведены в таблице 1.
Таблица 1
Значения базиса для функции ДОЛЯГОДА
| Базис | Способ вычисления дня |
| 0 или опущен | Американский (NASD) 30/360 |
| Фактический/фактический | |
| Фактический/360 | |
| Фактический/365 | |
| Европейский 30/360 |
Если базис < 0 или базис > 4, то функция ДОЛЯГОДА возвращает значение ошибки #ЧИСЛО!.
Результаты вычисления по формулам в среде Excel и расчетные формулы приведены на рис. 2.
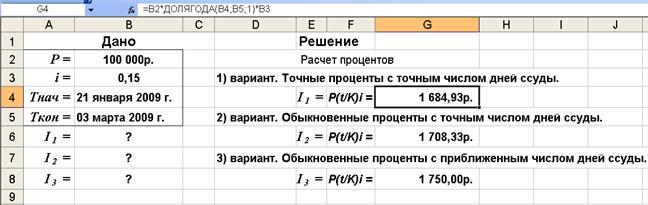
а) лист с результатами расчета
б) лист с расчетными формулами в режиме проверки формул
Рис. 2. Расчетные формулы и результаты вычислений в среде Excel
Числовой формат ячеек B4 и B5 задается с учетом выбора одного из возможных типов представления дат, приведенных в диалоговом окне Формат ячеек, рис. 3.
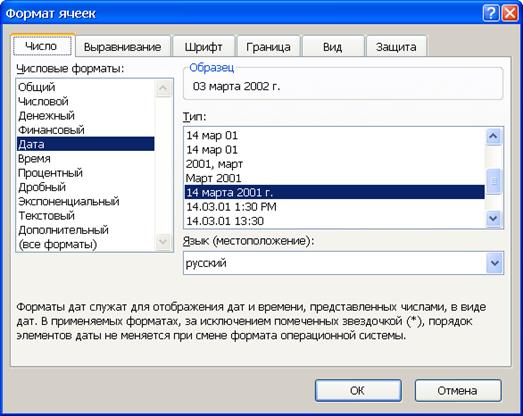
Рис. 3. Диалоговое окно Формат ячеек в среде Excel для выбора типа даты
3-й вариант.Вычисления с помощью встроенных функций Excel. Специальная финансовая функция в Excel для вычисления простых процентов отсутствует.
Простые переменные ставки
В кредитных соглашениях могут предусматриваться процентные ставки дискретно изменяющиеся во времени. В этом случае формула расчета наращенной суммы принимает следующий вид:
S = Р * (1+ n1 i 1+ n2 i2+... ) = Р*(1+ ∑nt i t ) ,(5)
где Р - первоначальная сумма (ссуда),
it - ставка простых процентов в периоде с номером t,
nt - продолжительность периода начисления t по ставке it.
Пример 3.В договоре, рассчитанном на год, принята ставка простых процентов на первый квартал в размере 16% годовых, причем в каждом последующем квартале она на 1% меньше, чем в предыдущем. Определить множитель наращения за весь срок договора.
Известны:
n1 = 0,25, i1 = 0,16 ;
n2 = 0,25, i2 = 0,15 ;
n3 = 0,25, i3 = 0,14 ;
n4 = 0,25, i4 = 0,13 .
Найти
(1+∑ntit ) = ? Решение.
1-й вариант.Вычисление множителя наращения производим по формуле (5) с помощью подручных вычислительных средств:
(1+∑ntit )= 1+0,25*0,16+0,25*0,15+0,25*0,14+0,25*0,13 =1,145.
2-й вариант.Вычисления в Excel выполнены по формуле (5) с использованием математической функции СУММПРОИЗВ приведены на рис. 4.
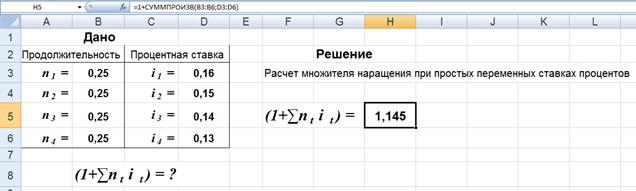
Рис. 4. Результаты вычислений множителя наращения. В ячейку Н5 введена формула: =1+СУММПРОИЗВ(B3:B6;D3:D6)
3-й вариант.Вычисления с помощью встроенных функций Excel. Специальная функция в Excel для вычисления простых процентов с переменными ставками отсутствует.
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. Последовательно воспользуемся формулами (7) и (6):
Р=S / (1 + ni ) = 1 000 000 / (1+0,20*90/360) = 952 380,95 руб.,
D=S - Р= 1 000 000 - 952 380,95 =47 619,05 руб.
2-й вариант.Вычисления в Excel выполнены по формулам (6) и (7), рис.7 .
Рис. 7. Результаты вычислений в среде Excel
3-й вариант.Вычисления с помощью встроенных функций Excel. Специальные функции в Excel для выполнения расчетов по операциям дисконтирования и учета по простым ставкам не предусмотрены.
Банковский или коммерческий учет (учет векселей) заключается в том, что банк до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца (являющегося кредитором) по цене ниже той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает (учитывает) его с дисконтом.
Для расчета процентов при учете векселей применяется учетная ставка, которая обозначается символом d. По определению, простая годовая учетная ставка находится по формуле:
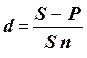(8)
Размер дисконта или учета, удерживаемого банком, равен
D = Snd,(9)
тогда векселедержатель получит сумму равную
P = S - D = S - Snd = S(1 -nd) = S(1 – (t/K) d )(10)
Множитель (1-nd )называется дисконтным множителем. Срок пизмеряет период времени от момента учета векселя до даты его погашения в годах. Дисконтирование по учетной ставке производится чаще всего при условии, что год равен 360 дням.
Пример 5. Через 90 дней предприятие должно получить по векселю 1 000 000 рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 20% годовых (год равен 360 дням). Определить дисконт D и полученную предприятием сумму P.
Известно:
S = 1 000 000 руб.,
n = 90 дней ,
d = 0,20 или 20% .
Найти
D = ?,P = ?
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств.
Для вычисления дисконта воспользуемся формулой (9)
D = Snd = 1 000 000 *(90/360) * 0,2 = 50 000 руб.
По формуле (10) рассчитаем сумму, которую предприятие получит в результате учета векселя:
P = S - D= 1 000 000 - 50 000 = 950 000 руб.
2-й вариант.Вычисления в Excel выполнены по формулам (9) и (10). Общий вид листа с расчетными формулами и результатами приведен на рис. 8.
Рис. 8. Результаты вычислений в среде Excel
3-й вариант.Вычисления с помощью встроенных функций Excel. Специальные функции в Excel для выполнения расчетов по операциям банковского и коммерческого учета с простыми учетными ставками не предусмотрены.
Сложные проценты
Сложные проценты применяются в долгосрочных финансово-кредитных операциях (сроком более 1 года), если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения называют капитализацией процентов.
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств по формуле (12):
П(1+ik )n k = (1+0,3)2 *(1+0,28) * (1+0,25)=2,704.
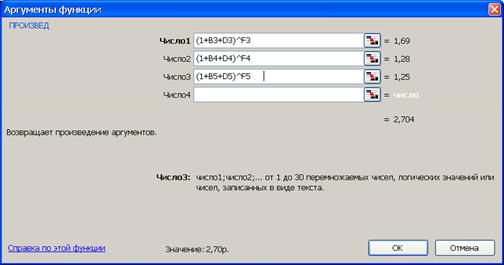
2-й вариант.Для выполнения расчетов по формулам воспользуемся функцией ПРОИЗВЕД (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.11.
а)
б)
Рис. 11. Результаты расчета множителя наращения (рис. а) и вид диалогового окна ПРОИЗВЕД с введенными данными (рис. б). В ячейку J4 введена формула =ПРОИЗВЕД((1+B3+D3)^F3;(1+B4+D4)^F4;(1+B5+D5)^F5)
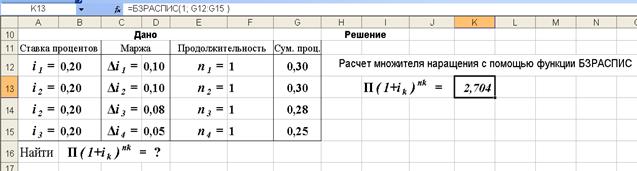
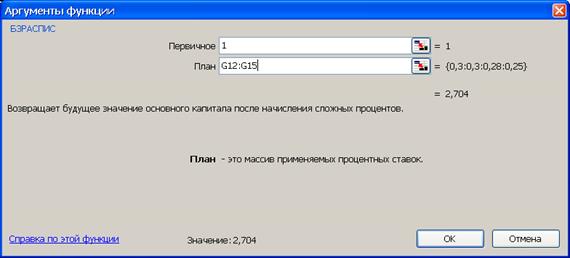
3-й вариант.Предварительно следует подготовить исходные данные по форме представленной на рис. 12а.Для выполнения расчетов следует воспользоваться функцией БЗРАСПИС (находится в категории Финансовые). Данная функция возвращает будущее значение основного капитала после начисления сложных процентов с переменной ставкой, рис.12. Поскольку здесь рассчитывается множитель наращения, то в качестве первоначальной суммы вводится 1 (см. рис 12б).
а)
б)
Рис. 12. Результаты расчета множителя наращения (рис. а) и вид диалогового окна БЗРАСПИС с введенными данными (рис. б). В ячейку J13 введена формула =БЗРАСПИС(1; G12:G15)
Синтаксис функции БЗРАСПИС (первичное; план). Аргументы функции:
первичное – действительное число, задающее первоначальную стоимость инвестиции;
план – массив значений, содержащих процентные ставки.
Напомним, что для вычисления будущей стоимости с постоянной ставкой используется функция БС.
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств проводим по формуле (15):
i э = (1 + j / m)m -1= (1+ 0,16 /4)4 - 1 = 0,170, или 17,0%.
2-й вариант.Расчет эффективной ставки выполним в Excel по формуле (15), результаты расчета представлены на рис. 15.
Рис. 15. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =(1+B3/B2) ^ B2-1
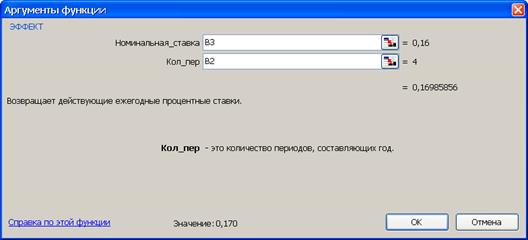
3-й вариант.Расчет эффективной ставки выполним в среде Excel с использованием функции ЭФФЕКТ (из категории Финансовые). Данная функция возвращает эффективную (фактическую) процентную ставку, при заданной номинальной процентной ставке и количестве периодов, за которые начисляются сложные проценты, рис.16.
а)
б)
Рис. 16. Результаты расчета эффективной ставки (рис. а) и вид диалогового окна ЭФФЕКТ с введенными данными (рис. б). В ячейку H3 введена формула =ЭФФЕКТ(B3;B2)
Синтаксис функции ЭФФЕКТ (номинальная_ставка;кол_периодов). Аргументы функции:
номинальная_ставка – значение номинальной процентной ставки,
кол_периодов – количество периодов начисления.
Обратная зависимость между номинальной и эффективной ставкой выражена следующей формулой:
j = m [(1+ iэ )1/m-1]. ( 16)
Пример 10.Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку в 12% годовых.
Известно:
iэ = 0,12 или 12% .
Найти j = ?
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств произведем по формуле (16):
j = m [(1+ iэ )1/m-1] =4*[ (1+0,12) (1/4) - 1 ] = 0,11495, или 11,495%.
2-й вариант.Для выполнения расчетов по формулам в среде Excel воспользуемся математической функцией СТЕПЕНЬ, рис. 17.
Рис. 17. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =B2*(СТЕПЕНЬ(1+B3;1/B2)-1)
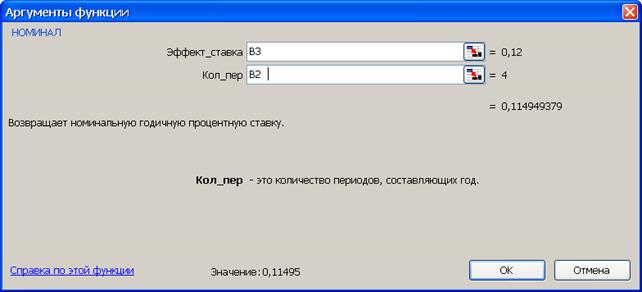
3-й вариант.Для выполнения расчетов номинальной ставки воспользуемся функцией НОМИНАЛ (из категории Финансовые). Данная функция возвращает номинальную годичную ставку при заданной эффективной ставке и числе периодов, за которые начисляются проценты. Результат расчета приведен на 18.
а)
б)
Рис. 18. Результаты расчета номинальной ставки (рис. а) и вид диалогового окна НОМИНАЛ с введенными данными (рис. б). В ячейку H3 введена формула =НОМИНАЛ(B3;B2)
Синтаксис функции НОМИНАЛ (эффект_ставка;кол_пер). Аргументы функции:
эффект_ставка – значение эффективной процентной ставки,
кол_пер – количество периодов начисления.
Решение.
1-й вариант.Вычисления с помощью подручных вычислительных средств выполним по формуле (17):
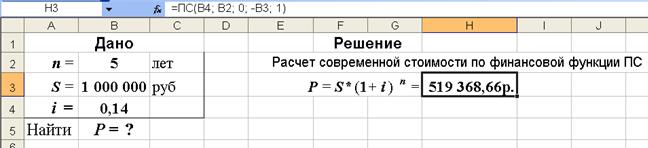
P = S/(1 + i ) n =1 000 000/(1+0,14) 5 = 519 368,66 руб.
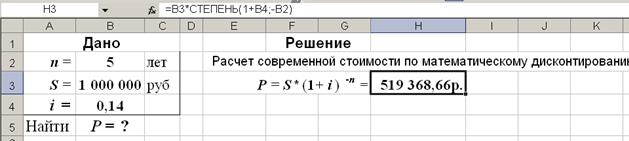
2-й вариант.Для выполнения расчетов в Excel по формулам воспользуемся математической функцией СТЕПЕНЬ. На рис. 19 приведены два варианта использования данной функции.
а)
б)
Рис. 19. Результаты расчета современной стоимости в среде Excel. В ячейку H3 введена формула: вариант а) =B3/СТЕПЕНЬ(1+B4;B2); вариант б) =B3*СТЕПЕНЬ(1+B4;-B2)
3-й вариант.Для выполнения расчетов по встроенным в Excel функциям воспользуемся финансовой функцией ПС, рис. 20. Данная функция возвращает приведенную стоимость инвестиции при условии периодических равных по величине платежей и постоянной процентной ставки.
а)
б)
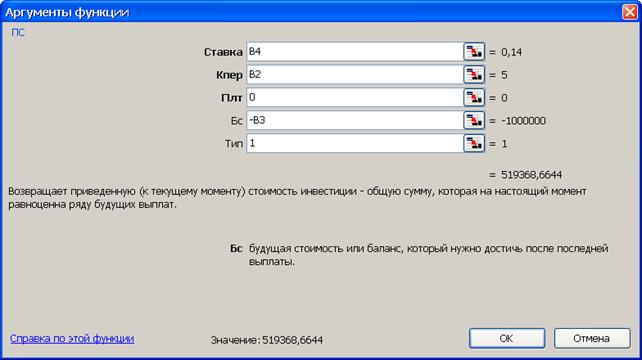
Рис. 20. Результаты расчета современной стоимости (рис. а) и вид диалогового окна ПС с введенными данными (рис. б). В ячейку H3 введена формула =ПС(B4; B2; 0; -B3; 1)
Синтаксис функции ПС (ставка;кпер;плт;бс;тип). Аргументы функции:
ставка – значение процентной ставки за один период,
кпер – количество периодов начисления,
плт – величина платежа (можно опускать, когда аргумент принимает нулевое значение),
бс – необязательный аргумент, задает будущую стоимость или остаток средств после последней выплаты;
тип – необязательный аргумент (принимает значения 0, когда выплаты производятся в конце периода, 1- в начале периода).
При начислении процентов т раз в году, используется формула:
P = S / (1 + j / m) nm = Sν nm , (19)
где ν nm = 1/(1 + j / m) nm (20)
(дисконтный множитель).
Величину Р, полученную дисконтированием S, называют современной, илитекущей стоимостью,илиприведенной величиной S.
Суммы Ри Sэквивалентны в том смысле, что платеж в сумме S через плет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S - Pназывается дисконтом.
Банковский учет.В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле:
Р = S(1- dсл )n(21)
где dcл1 - сложная годовая учетная ставка.
Дисконт в этом случае будет равен:
D = S – P = S – S(1- dсл)n = S[1– (1 - dсл)n] (22)
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.
Пример 12.Через 5 лет по векселю должна быть выплачена сумма 1 000 000 руб. Банк учел вексель по сложной учетной ставке в 10% годовых. Определить сумму, которую получит векселедержатель и дисконт, который получит банк по истечении срока векселя.
Известно:
n = 5 лет,
S = 1 000 000 руб.,
i = 0,14 или 14% .
Найти P = ?, D = ?
Решение.
1-й вариант.Вычисления по формулам (21 и 22) с помощью подручных вычислительных средств.
Расчет сумы, которую получит векселедержатель по формуле (21)
Р = S(1- dсл )n =1 000 000 * (1 - 0,10) 5 = 590 490,00 руб.;
Расчет дисконта, который получит банк, произведем по формуле (22)
D = S - Р= 1 000 000 - 590 490 = 409 510 руб.
2-й вариант.Расчеты в Excelпо формулам (21 и 22) с использованием математической функции СТЕПЕНЬ, рис. 21.
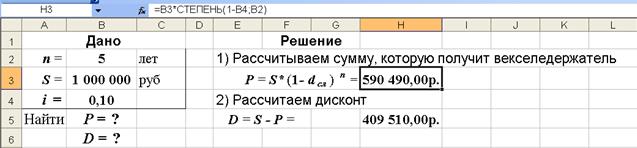
Рис. 21. Результаты расчета значений P и D в среде Excel. В ячейку H3 введена формула =B3*СТЕПЕНЬ(1-B4; B2)
3-й вариант.Вычисления с помощью встроенных функций Excel. Готовые финансовые функции для решения подобных задач в Excel не найдены.
Потоки платежей
Решение
1-й вариант.Вычисления с помощью подручных вычислительных средств проведем по формуле (1.25):
S = (10 000 000/4) * [(1+0,1) 3 - 1]/ [(1+0,1) 1/4 - 1] =34 316 607,35 руб.
2-й вариант.Для выполнения расчетов по формулам в среде Excel используем математическую функцию СТЕПЕНЬ, рис. 25.
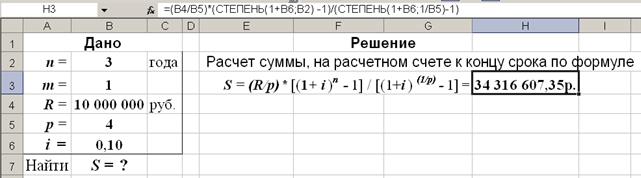
Рис. 25. Результаты расчета в Excel (в ячейку H3 введена формула: =(B4/B5)*(СТЕПЕНЬ(1+B6;B2) -1)/(СТЕПЕНЬ(1+B6;1/B5)-1) )
3-й вариант.Вычисления с помощью встроенных функций Excel. В Excel отсутствуют готовые финансовые функции для решения подобных задач.
Пример 16.В течение 3-x лет на расчетный счет в конце каждого квартала поступают платежи равными долями из расчета 10 млн руб. в год (т.е. по 10/4 млн руб. в квартал), на которые ежеквартально начисляются проценты по сложной ставке в 10% годовых. Определить сумму на расчетном счете к концу указанного срока.
Известно:
n = 3 года,
p = m = 4,
R= 10 000 000 руб.,
j = 0,10 .
Найти S = ?
Решение
1-й вариант.Вычисления с помощью подручных вычислительных средств произведем по формуле (26):
S = 10 000 000*[(1+0,1/4) ( 4*3 ) - 1] / 0,1 = 34 488 882,42 руб.
2-й вариант.Для выполнения расчетов по формулам в Excel воспользуемся функцией СТЕПЕНЬ, рис. 30.
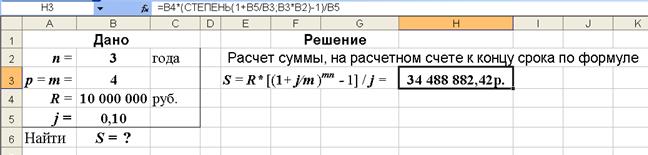
Рис. 26. Результаты расчета в Excel (в ячейку H3 введена формула: =B4*(СТЕПЕНЬ(1+B5/B3;B3*B2)-1)/B5) )
3-й вариант.Вычисления с помощью встроенных функций Excel. Для расчета наращенной суммы S воспользуемся функцией БС (из категории Финансовые). Данная функция возвращает, будущую стоимость инвестиции на основе периодических равных по величине платежей и постоянной процентной ставке, рис. 27.
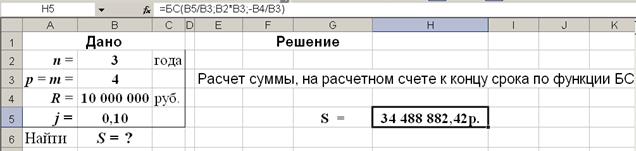
Рис. 27. Результаты расчета наращенной суммы S ( в ячейку H5 введена формула: =БС(B5/B3;B2*B3;-B4/B3) )
Рента р - срочная, с произвольным поступлением платежей p ≥ 1, и произвольным начислением процентов m ≥ 1 (общий случай). Это самый общий случай р-срочной ренты с начислением процентов траз в году, причем, возможно, р ≠ т.
Первый член ренты R/p, уплаченный спустя 1/р года после начала, составит к концу срока вместе с начисленными на него процентами
= 
.
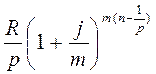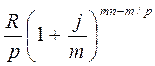Второй член ренты к концу срока возрастет до
= 
,
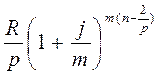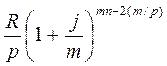и т.д.
Последний член этой записанной в обратном порядке геометрической прогрессии равен R/p, ее знаменатель (1+j/m)m/p,число членов пт.
Для данного случая наращенная сумма рассчитывается по формуле:
S =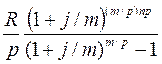 
= 
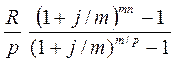. (27)
Из последней формулы легко получить все рассмотренные выше частные случаи, задавая соответствующие значения р и т.
Пример 17.В течение 3-х лет на расчетный счет в конце каждого квартала поступают платежи (р=4) равными долями из расчета 10 млн руб. в год (т.е. по 10/4 млн руб. в квартал), на которые ежемесячно (m=12) начисляются проценты по сложной ставке в 10% годовых. Определить сумму на расчетном счете к концу указанного срока.
Известно:
n = 3 года,
m = 12,
R= 10 000 000 руб.,
p = 4,
j = 0,10 .
Найти S = ?
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (1.27) находим:
S = (10 000 000/4)*[(1+0,10/4)(3*12) -1] / [(1+0,10/4)(12/4) -1] =
= 34 529 637,96 руб.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу соответствующую (27) и для вычисления степени используем функцию СТЕПЕНЬ, рис. 28.
Рис. 28. Результаты расчета в Excel (в ячейку H3 введена формула: =(B4/B5)*(СТЕПЕНЬ(1+B6/B3;B3*B2) -1)/(СТЕПЕНЬ(1+B6/B3;B3/B5)-1) )
3-й вариант.Вычисления с помощью встроенных функций Excel. В Excel отсутствуют готовые финансовые функции для решения подобных задач.
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (30) находим:
R= (10 000 000*0,14)/[1-1/(1+0,14)3] = 4 307 314,80 руб.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (30). Для вычисления степени используем математическую функцию СТЕПЕНЬ, рис. 33.
Рис. 33. Результаты расчета в Excel отдельного платежа R простой ренты постнумерандо по формуле (в ячейку H5 введена формула:
=(B3*B4)/(1-1/СТЕПЕНЬ(1+B4;B2)))
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции ПЛТ (категория Финансовые), рис. 34.
Рис. 34. Результаты расчета в Excel величины отдельного платежа R простой ренты A с использованием функции ПЛТ (в ячейке Н5 записана формула: ПЛТ(B4;B2;-B3; ) )
Определение величины отдельного платежа R по схеме пренумерандо. В этом случае для расчета отдельного платежа используется следующая формула:
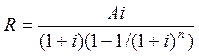(31)
Пример 21.Для условийпримера 1.20рассчитать размер ежегодных погасительных платежей, если они будут выплачиваться в начале года.
Известно:
n = 3 года,
A= 10 000 000 руб.,
i = 0,14 .
Найти R = ? Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (31) находим:
R= (10 000 000*0,14)/[(1+0,14)(1-1/(1+0,14)3)] = 3 778 346,32 руб.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (31) и для вычисления степени используем функцию СТЕПЕНЬ, рис. 35.
Рис. 35. Результаты расчета в Excel отдельного платежа R ренты пренумерандо (в ячейку H4 введена формула:
=(B3*B4)/((1+B4)(1-1/СТЕПЕНЬ(1+B4;B2))) )
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции ПЛТ (категория Финансовые), рис. 36.
Рис. 36. Результаты расчета в Excel величины отдельного платежа R простой ренты с использованием функции ПЛТ
(в ячейке Н5: ПЛТ(B4;B2;-B3; ;1)
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (33) находим:
n = ln(1+30 000 000*0,15/(5 000 000*(1+0,15)) / ln(1+0,15) = 4,14 года.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (33) и для вычисления степени используем логарифмическую функцию LN, рис. 39.
Рис. 39. Результаты расчета в Excel срока ренты n пренумерандо по известной наращенной сумме S (в ячейку H4 введена формула: =LN(1+B3*B4/(B2*(1+B4)))/LN(1+B4) )
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции КПЕР (категория Финансовые), рис. 40.
Рис. 40. Результаты расчета в Excel срока простой ренты n по известной будущей стоимости S с использованием функции КПЕР (в ячейку Н4 введена функция КПЕР(B4;-B2; ;B3;1) )
2-й случай.Определение срока простой ренты n при известной современной стоимости ренты A
Срок простой ренты при платежах по схеме постнумерандо определяется по следующей формуле:
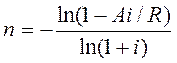. (34)
Пример 24. Организация взяла кредит в размере 30 000 000 руб. с условием погашения ежегодными платежами по 6 000 000 руб. в конце года (постнумерандо) и начислением по сложной процентной ставке 15% годовых. Определить срок простой ренты.
Известно:
A= 30 000 000 руб.,
R = 6 000 000 руб.,
i = 0,15 .
Найти n = ? Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (34) находим:
n= - ln (1-30 000 000*0,15/6 000 000) / ln(1+0,15) = 9,92 года.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (34) и для вычисления степени используем функцию LN (категория Математические), рис. 41.
Рис. 41. Результаты расчета в Excel срока ренты n постнумерандо по известной современной стоимости A простой ренты (в ячейку H4 введена формула: = - LN(1-B2*B4/B3)/LN((1+B4) )
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции КПЕР (категория Финансовые), рис. 42.
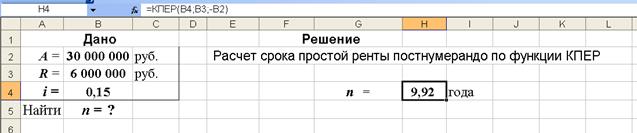
Рис. 42. Результаты расчета в Excel срока простой ренты n постнумерандо с использованием функции КПЕР (в ячейке Н4: КПЕР(B4;B3;-B2) )
В случае, когда реализуется рента пренумерандо, то срок ренты рассчитывается по выражению:
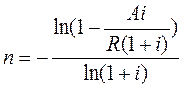(35)
Пример 25. Для условий задачи 24 определить сроки простых рент пренумерандо.
Решение.
1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. По формуле (35) находим:
n = - ln (1-30 000 000*0,15/(6 000 000*(1+0,15)) / ln(1+0,15) = 7,56 года.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводим формулу (35) и для вычисления степени используем функцию логарифмирования LN (категория Математические), рис. 43.
Рис. 43. Результаты расчета в Excel срока ренты n пренумерандо по известной современной стоимости A простой ренты (в ячейку H4 введена формула: = - LN(1-B2*B4/(B3(1+B4)))/LN(1+B4) )
3-й вариант. Вычисления с помощью встроенных функций Excel. Выполним расчеты с использованием функции КПЕР (категория Финансовые), рис. 44.
Рис. 44. Результаты расчета в Excel срока простой ренты n пренумерандо с использованием функции КПЕР (в ячейке Н4: КПЕР(B4;B3;-B2;;1) )
Решение
1-й вариант.Вычисления по формуле (37) с помощью подручных вычислительных средств:
А = (10 000 000/4)*[1 - (1+0,1/12) (-12*3)]/[(1+0,1/12)](12/4) -1] =
= 25 612 003,42 руб.
2-й вариант.Для выполнения расчетов по формулам в среде Excel в строку формул вводится формула (37) с использованием математической функции СТЕПЕНЬ, рис. 48.
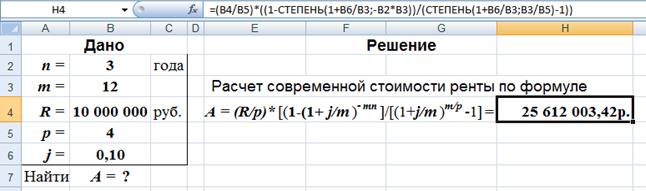
Рис. 48. Результаты расчета в Excel (в ячейку H4 введена формула: =(B4/B5)*((1-СТЕПЕНЬ(1+B6/B3;-B2*B3))/(СТЕПЕНЬ(1+B6/B3;B3/B5)-1)) )
3-й вариант. Вычисления с помощью встроенных функций Excel. Для решения этой задачи в среде Excel финансовую функцию подобрать не удалось.
ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ
Задача 1. Выполнить различные коммерческие расчеты, используя данные, приведенные в таблице. Номер варианта соответствует последней цифре зачетной книжки.
Варианты для самостоятельного решения
| Вари- ант | Первонач. сумма, руб. | Наращен. сумма, руб. | Дата начала, | Дата конца, | Время, дн. | Время, лет | Ставка, % | Число начислений процентов |
| P | S | Tн | Tк | Tдн | n | i | m | |
| 10 000 000 | 500 000 | 23.01.2009 | 17.03.2009 | 8,0 | ||||
| 9 800 000 | 1 000 000 | 24.01.2009 | 18.03.2009 | 8,5 | ||||
| 9 600 000 | 1 500 000 | 30.01.2009 | 19.03.2009 | 9,0 | ||||
| 9 400 000 | 2 000 000 | 31.01.2009 | 20.03.2009 | 9,5 | ||||
| 9 200 000 | 2 500 000 | 01.02.2009 | 15.03.2009 | 10,0 | ||||
| 9 000 000 | 3 000 000 | 28.01.2009 | 16.03.2009 | 10,5 | ||||
| 8 800 000 | 3 500 000 | 29.01.2009 | 11.03.2009 | 11,0 | ||||
| 8 600 000 | 4 000 000 | 25.01.2009 | 12.03.2009 | 11,5 | ||||
| 8 400 000 | 4 500 000 | 27.01.2009 | 13.03.2009 | 12,0 | ||||
| 8 200 000 | 5 000 000 | 26.01.2009 | 14.03.2009 | 12,5 |
Расчеты выполнить в среде Excel по второму варианту (с помощью формул) и по третьему варианту (по встроенным функциям, где это возможно) решений, подобно рассмотренным в практикуме примерам.
Задание 1.1. Банк выдал ссуду, размером S руб. Дата выдачи ссуды - Тн, возврата – Тк. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке i % годовых. Найти:
1.1) точные проценты с точным числом дней ссуды;
1.2) обыкновенные проценты с точным числом дней ссуды ;
1.3) обыкновенные проценты с приближенным числом дней ссуды.
Задание 1.2. Через Тдн дней после подписания договора, должник уплатит S рублей. Кредит выдан под i % годовых (проценты обыкновенные). Какова первоначальная сумма и дисконт?
Задание 1.3. Через Тдн дней предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке i % годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт?
Задание 1.4. В кредитном договоре, на сумму S рублей и сроком на Тлет лет, зафиксирована ставка сложных процентов, равная i % годовых. Определить наращенную сумму.
Задание 1.5. Ссуда, размером S рублей предоставлена на Тлет лет. Проценты сложные, ставка – i % го