Понятие, сущность и виды инфляции

Инфляция представляет собой обесценение денег, падение их покупательной способности, вызываемое повышением цен, товарным дефицитом и снижением качества товаров и услуг.

Суть инфляции можно понять, связывая ее с нарушением закона денежного обращения и прежде всего несовпадением динамики денежной массы и номинального ВНП.

При опережающих темпах роста денежной массы по сравнению с увеличением номинального ВНП возникают инфляционные процессы, а при обратном соотношении рассматриваемых показателей – дефляция.

Виды инфляции:

1. Подавленная (скрытая) инфляция – выражается в том, что за прежние суммы приобретается продукция более низкого качества и в меньшем количестве, происходит более быстрый рост цен на новые изделия по сравнению с качеством, из торговли «вымывается» более дешевый ассортимент.

2. Инфляция спроса – обуславливается «разбуханием» денежной массы и в связи с этим платежеспособного спроса при данном уровне цен в условиях недостаточно эластичного производства, способного быстро реагировать на потребности рынка.

3. Инфляция издержек - рост цен под воздействием растущих издержек производства, прежде всего роста затрат на заработную плату. Рост цен требует увеличения заработной платы, увеличение заработной платы влечет за собой повышение цен – это теория «инфляционной спирали и заработной платы». При такой инфляции совокупный спрос практически не растет, а издержки и цены повышаются.

Индексы

Измерение уровня инфляции

Базовыми показателями, которые используют для измерения уровня инфляции, служат индексы цен.

Виды индексов цен.

1. Индексы оптовых цен – показывают изменения среднего уровня цен реализации продукции промышленных, торговых и сельскохозяйственных предприятий (но не оптовой торговли);

2. Индексы розничных цен – рассчитывают либо как совокупный индекс цен на продукцию, продаваемую в розничной торговле, либо только по корзине специально значимых товаров. Второй из этих индексов означает «стоимость жизни» в стране особенно важен ля населения.

3. Дефлятор ВНП – определяется по объему конечной продукции, которая формирует стоимость ВНП, в том числе по ценам на важнейшие товары, покупаемые населением, оборудование и другие основные средства, покупаемые фирмами, тарифам на услуги, оказываемые государственному сектору, а также внешнеторговым ценам. Исключаются только цены на промежуточные продукты, которые служат в качестве оборотных средств. Эти индексы являются важнейшими показателями, т.к. отражают действительный уровень инфляции в стране.

Наиболее известные для расчета индекса цен формулы:

1. Формула Ласпейреса

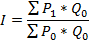
2. Формула Пааше

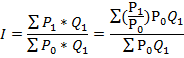
3. Формула Фишера

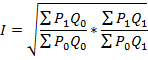
где Р₁ и Р₀ – цены текущего и базисного периодов;

Q₁ и Q_{2 –} количество продукции в текущий и базисный периоды.

Пусть выбран определенный набор товаров и услуг и пусть за время t его стоимость изменилась от суммы Р₁ до суммы Р₂.

Пусть индекс цен будет выражаться формулой:

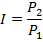
Темпом инфляции за время t называется величина

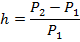
Темп инфляции (умноженный на 100) показывает, на сколько процентов выросли цены за период времени t.

Соотношение между индексом цен и темпом инфляции:

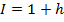
Например, если I=2,4, то h=1,4, т.е. цены за рассматриваемый период выросли в 2,4 раза, или, что эквивалентно, на 140%.

Индекс цен за данный период показывает, во сколько раз выросли цены по отношению к уровню цен предыдущего года.

Если известны индексы цен 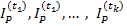(или темпы инфляции 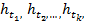) за периоды времени t₁, t₂, …, t_k и эти периоды расположены последовательно друг за лругом, то индекс цен за время t = t₁+t₂+…+t_k будет равен

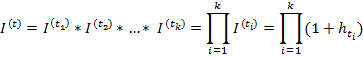
Знак 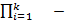обозначается умножение.

Если за время t была получена некоторая наращенная сумма FV, а индекс цен составил величину I^(t), то эта сумма с учетом ее обесценения составит:

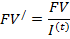
Например при годовой инфляции 20% сумма в 3 тыс. руб. через год по своей покупательной способности в ценах текущего дня (т.к. t=1, h₁=0,2, I=1,2) составит величину

Простые проценты и инфляция

Пусть на капитал PV происходит начисление простых процентов по ставке r в течение времени n и индекс цен за это врем равен I⁽ⁿ⁾, тогда, учитывая обесценение денег за это время получим:

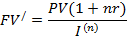
где 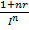– множитель наращения простых процентом инфляции.

Из формулы следует, что реальное наращение первоначального капитала с учетом покупательной способности денег будет только в том случае, если 1+nr>I⁽ⁿ⁾

Если 1+nr=I⁽ⁿ⁾ , то наращение только компенсирует действие инфляции

Из равенства 1+nr=I⁽ⁿ⁾ найдем r

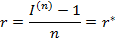
где r^* - минимально допустимая процентная ставка, при которой не происходит реального уменьшения капитала (эрозии капитала).

Ставка, превышающая r* называется положительной процентной ставкой, т.к. только при ее применении будет происходить реальное увеличение капитала.

Брутто – ставка (r^/) – ставка процентов, индексированная с учетом роста уровня цен для учета инфляции

Для обеспечения полной компенсации негативного воздействия инфляции и получения доходности согласно первоначальной ставке r, размер брутто – ставки r^/ определяется из равенства

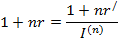
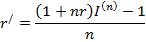
Если задана брутто – ставка r^/ (т.е. объявлена норма доходности), то можно определить реальную процентную ставку, т.е. доходность с учетом инфляции при начислении простых процентов

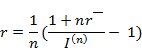
Т.о. при инфляции различают следующие виды процентных ставок

Номинальная процентная ставка – это исходная базовая (как правило годовая) процентная ставка, указанная в договорах. Доходность, выражаемая этой ставкой, не скорректирована на инфляцию.

Реальная процентная ставка - показывает доходность с учетом инфляции, характеризующейся снижением покупательной способности денег. В условиях инфляции она всегда меньше номинальной процентной ставки и может быть даже отрицательной.

Положительная процентная ставка - это любая ставка, при которой будет происходить реальное увеличение стоимости капитала при данном индексе инфляции.

Брутто – ставка процента – ставка процента, индексированная с учетом роста уровня цен для учет инфляции (ставка при которой капитал действительно растет с необходимой доходностью) .

В условиях галопирующей инфляции (15-20% в год) используется и плавающая процентная ставка.

При начислении процентов на вклады и кредиты сроком до года применяется формула 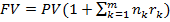, которую можно записать в виде:

где t_k – продолжительность в днях периода, на который установлена процентная ставка r_k,

Т - количество дней в году.

Величина учетной ставки d^/, компенсирующей инфляционные потери, определяется из равенства:

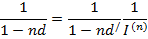
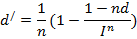
Если задана ставка d^/ , то из последнего равенства можно определить реальную учетную ставку, позволяющую оценить соответствующим образом доходность при инфляции

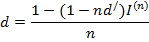
Если индекс цен меньше единицы, то это свидетельствует о дефляции.

Сложные проценты и инфляция

Пусть на капитал PV в течение n лет начисляются сложные проценты и индекс цен за это время равен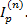

FV=PV*cⁿ, 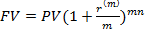= PV*cⁿ.

где m - количество начислений в год.

Но с учетом инфляции:

(*)

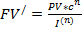Отсюда ясно, что для того, чтобы не происходило эрозии капитала должно выполняться неравенство сⁿ≥I⁽ⁿ⁾, что равносильно неравенству

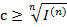
причем если , то наращение капитала лишь нейтрализует действие инфляции.

Ставка, для которой соответствующий коэффициент с превышает с^*, называется положительной ставкой.

Например, если 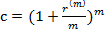, то положительная процентная ставка определяется из неравенства , откуда следует

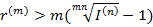
Если в течение n лет ожидаемый ежегодный индекс инфляции равен I, то I=1+h, I⁽ⁿ⁾=(I)ⁿ=(1+h)ⁿ, где h – ожидаемый ежегодный темп инфляции.

Тогда .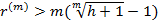

Если сложные проценты начисляются один раз в год, то должно быть r^(m)=r>h, т.е. процентная ставка должна превышать темп инфляции.

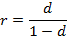
Полагая, что , находим, что положительная учетная ставка удовлетворяет неравенству 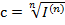, , 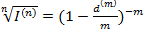, 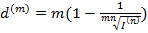а при m=1 и I⁽ⁿ⁾=(1+h)ⁿ получим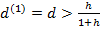

Для обеспечения реального роста стоимости первоначального капитала необходимо исходную ставку увеличивать (индексировать). Выбор величины такой индексированной ставки, называемой брутто-ставкой, определяется поставленными целями.

Для обеспечения реальной доходности согласно коэффициенту наращения с необходимо так индексировать исходную ставку (увеличивать на инфляционную премию), чтобы новый коэффициент наращения с^/ полностью компенсировал потери из-за инфляции. Т.о., с^/ определяется из равенства:

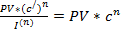, Þ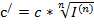

Размер брутто – ставки (r^/) обеспечивает полную компенсацию негативного воздействия инфляции и получение доходности. Следовательно в формуле (*) множитель сⁿ нужно приравнять к множителю , тогда если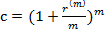

,

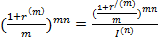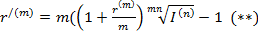– брутто ставка наращения

Задавая брутто- ставки в формуле (**) можно определить реальную ставку наращения r^(m) (выразим из (**) r^(m))

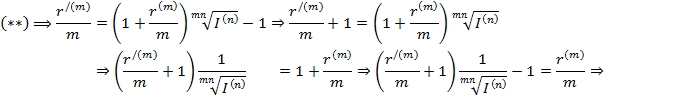
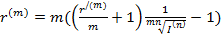- реальная ставка наращения

Выводим формулы для определения реальной брутто – ставки d^/(m) и реальной учетной ставки d^(m)

Если , то с учетом (*)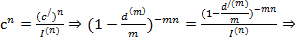

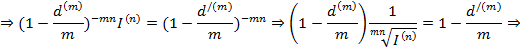
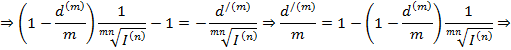
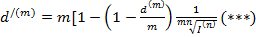- учетная брутто ставка

Из формулы (***) можно выразить реальную учетную ставку d^(m)

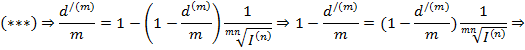
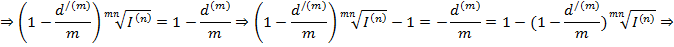
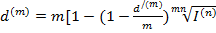- реальная учетная ставка

Формула Фишера И.

При I⁽ⁿ⁾=(1+h)ⁿ и m=1 из (**) r^(1)/=r^/ получаем (обозначая r⁽¹⁾=r)

r^/=r+h+rh

где h+rh - инфляционная премия, которую нужно прибавить к исходной ставке доходности для компенсации инфляционных потерь

вывод формулы: