Дисконтирование векселей по сложной учетной ставке
В случае если сложный процент начисляется в момент заключения финансового соглашения осуществляется операция дисконтирования и применяется сложная учетная ставка.
Предположим, что некоторое долговое обязательство на сумму FV и сроком погашения через n лет продается (учитывается) раньше срока с дисконтом по сложной годовой учетной ставке d.
Если осуществить продажу (учет) за год до срока то начисляются проценты FV*d и продавец получит сумму
FV-FV*d=FV(1-d)
Если осуществить продажу за два года до срока погашения, то за один год проценты начисляются на FV, а за второй год – уже на сумму FV(1-d), дисконтированную на предыдущем шаге, т.е. продавец получит сумму
FV(1-d)-FV(1-d)d=FV(1-d)(1-d)=FV(1-d)2
Если долговое обязательство продается за n лет до срока, то продавец получит сумму
PV=FV(1-d)n
где (1-d)n – дисконтный множитель.
PV представляет собой текущую (современную) стоимость будущего платежа FV.
Дисконт D равен величине
D=FV-PV=FV-FV(1-d)n=FV(1-(1-d)n)
Если срок n, за который осуществляется дисконтирование не является целым числом лет, то возможны следующие методы определения стоимости учтенного за n лет капитала:
а) использование сложной учетной ставки
PV=FV(1-d)a+b
б) использование смешанной схемы
PV=FV(1-d)a(1-bd)
где a – целое число лет, а = [n],
b – дробная часть года, b=n-[n], n=a+b
Пусть дисконтирование происходит m раз в году и задана сложная годовая учетная ставка d(m)/
Если капитал учитывается за n лет при m-кратном дисконтировании в течение года
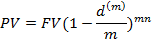
Если mn не является целым числом. Это возможно тогда, когда дисконтирование осуществляется по внутригодовым подпериодам, но общий период n неравен целому числу подпериодов. В этом случае можно использовать следующие формулы:
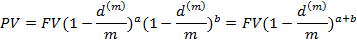
или
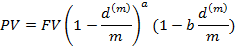
где a=[nm], b=nm-[nm],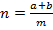 
Из формулы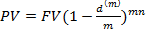 
определяется период n
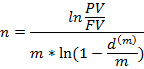
При m=1, d(m)=d
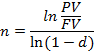
Из этой же формулы определяется величина номинальной учетной ставки d(m)
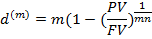
При m=1, d(m)=d,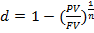 
Определение эффективной годовой учетной ставки dэ, обеспечивающей переход от FV к PV при заданных их значениях и однократном дисконтировании
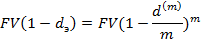
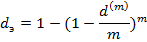
Из формулы определения dэ можно найти соотношение для определения номинальной учетной ставки, если известны dэ и число m дисконтирования в год.
Используя эффективную учетную ставку можно определить эквивалентные номинальные учетные ставки d(m) и d(l) как ставки, удовлетворяющие равенствам:
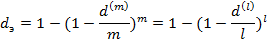
Эффективную годовую учетную ставку можно найти, не зная номинальной учетной ставки, а зная величину FV и ее дисконтированную (любым образом) за время n сумму PV.
Если PV=FV(1-dэ)n, то
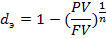
Если наращение сложными процентами по учетной ставке происходит m раз в год, то можно из формулы 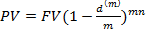вывести формулу для определения наращенной суммы
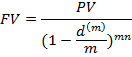
Тема 8. Финансово – экономические расчеты при операциях с облигациями
8.1.Основные определения и формулы
Понятие облигации
Под облигацией понимается ценная бумага, свидетельствующая о том, что ее держатель предоставил заем эмитенту этой бумаги.
Фундаментальные свойства облигаций:
1. Наличие конечного срока действия облигации. При выпуске облигаций эмитент в проспекте эмиссии указывает срок погашении облигации, при наступлении которого предприятие выкупает свои облигации у инвесторов, выплачивая им номинальную стоимость облигации.
2. Владельцы облигации, как кредиторы, имеют приоритет в получении дохода:
- выплаты в пределах установленного норматива являются частью издержек предприятия и включаются в себестоимость (по облигациям эмитент даже при отсутствии прибыли обязан выплачивать доход);
- выплаты по облигациям являются обязанностью эмитента, которую он принял на себя, выпустив облигации в обращение (выплаты дивидендов по акциям не является жестким обязательством эмитента, по облигациям выплата процентов является обязательной);
3. Наличие у владельцев облигаций права на первоочередное удовлетворение их требований по сравнению с акционерами при ликвидации предприятия. Владельцы облигаций являются кредиторами. Поэтому в случае ликвидации предприятия им будет погашена вся задолженность по текущим платежам за истекший период и выплачена номинальная стоимость облигации. Расчеты же с акционерами производятся после погашения задолженности перед всеми кредиторами.
Основные параметры облигации:
- номинальная цена (номинал);
- выкупная цена или правило ее определения если она отличается от номинала;
- дата погашения;
- норма доходности или купонная процентная ставка;
- даты выплат процентов.
Виды облигаций:
1. По методу обеспечения:
Закладные (обеспеченные) облигации – выпускаются под залог конкретного имущества:
- ипотечные облигации (выпущены под залог земли или недвижимости);
- облигации с переменным (плавающим) залогом (в качестве обеспечения выступают машины, оборудование, материалы, стоимость которых подвержена колебаниям во времени);
- облигации под залог ценных бумаг.
Бесзакладные (необеспеченные) облигации – это прямые долговые обязательства компании, которые не обеспечены никаким залогом.
2. По способу получения дохода:
Купонные облигации – облигации, к которым прилагаются купоны с указанием на них процента доходности и даты выплаты дохода (облигации с фиксированным и плавающим купоном)
Дисконтные – облигации, по которым проценты не выплачиваются, а владелец облигации получает доход за счет того, что облигация продается с дисконтом, т.е. по цене ниже номинала. Выкуп облигации осуществляется по номинальной стоимости за счет чего их владельцы получают соответствующий доход.
3. Индексируемые облигации – выпускаются с целью защиты инвестора от обесценения облигаций в связи с инфляцией, изменением валютного курса и т.д. Отличительной чертой индексируемых облигаций является то, что сумма выплат по купону и номинальная стоимость облигаций корректируется на специальный коэффициент, отражающий изменение соответствующего показателя (темп инфляции, динамика валютного курса и т.д.)