Элементарные методы обработки расчетных данных

При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами: во-первых, величинами, которые характеризуют ряд значений как целого, т.е. характеристиками общности, во-вторых, величинами, которые описывают различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.

Разумеется, все средние величины относятся к первой группе показателей, поскольку являются характеристиками изучаемой совокупности как целого. Кроме того, в качестве показателей общности используются следующие величины: середина интервала, мода и медиана.

Середина интервала возможных значений x_i рассчитывается по формуле:

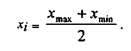
Мода - такое значение изучаемого признака, которое среди всех его значений встречается наиболее часто. Если чаще других встречаются два или более различных значений, такую совокупность данных называют бимодальной или мультимодальной. Если же ни одно из значений не встречается чаще других (т.е. если все значения встречаются по одному разу или равное количество раз), такая совокупность является безмодальной.

Медиана - такое значение изучаемой величины, которое делит изучаемую совокупность на две равные части, в которых количество членов со значениями меньше медианы равно количеству членов, которые больше медианы. Медиану можно найти только в совокупностях данных, содержащих нечетное количество значений. Только тогда и слева, и справа от медианного значения будет одинаковое число членов.

В отличие от средней, величина медианы не зависит от крайних значений показателей. Например, если максимальное значение изучаемого показателя увеличится, то все средние возрастут вместе с ним, медиана же останется неизменной. Поэтому она является более удобной характеристикой совокупности в тех случаях, когда совокупность данных неоднородна и имеет резкие "выбросы" в сторону минимума или в сторону максимума.

В качестве показателей размаха и интенсивности вариации показателей чаще всего используются следующие величины: размах вариации, среднее линейное отклонение, среднеквадратическое отклонение, дисперсия и коэффициент вариации.

Размах вариации рассчитывается по формуле:

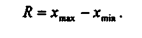
Среднее линейное отклонение (средний модуль отклонения) от среднего арифметического исчисляется по формуле:

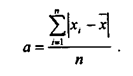
Если используются весовые коэффициенты, то формула средневзвешенного среднего линейного отклонения имеет вид:

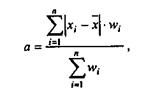
где w_i - частота, с которой в изучаемой совокупности встречается значение x_i.

Наибольшее распространение при изучении разброса значений числовых данных получили величины среднеквадратического отклонения (СКО) σ и дисперсии σ²:

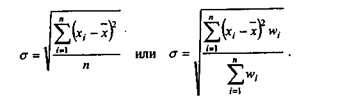
Чем больше величина σ или σ², тем сильнее разброс значений вокруг среднего. Следует отметить, что σ всегда больше модуля среднего линейного отклонения. Для нормально распределенных величин σ/а 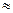1,2. Если же такое соотношение не выполняется, это свидетельствует о том, что в исследуемом массиве данных есть элементы, неоднородные с основной массой, сильно выбивающиеся по своей величине из общего ряда. В зависимости от природы решаемой задачи следует подумать об исключении этих единиц из рассмотрения вообще либо не использовать их при построении некоторых моделей, поскольку они являются в своем роде исключениями из общего правила.

Величина СКО, как следует из ее определения, зависит от абсолютных значений самого изучаемого признака. Чем больше величины x_i, тем больше будет σ. Поэтому для сравнения рядов данных, отличающихся по абсолютным величинам, вводят коэффициент вариации:

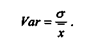
Этот коэффициент является показателем "количественной" неоднородности совокупности данных. Критическое значение его считается равным 33%. Если Vаr > 33%, то совокупность нельзя признать однородной.

Использование коэффициента вариации в анализе данных, касающихся финансово-хозяйственной деятельности торговой сети, рассмотрим на примере 2.12.

Пример 2.12.Торговая сеть "Океан" включает 10 магазинов и специализированных отделов в универсамах города. Имеются данные о выручке (R) и среднегодовой стоимости основных средств (ОФ) каждого из магазинов за 1998 и 1999 гг. (тыс. руб.). На основании этих данных требуется сделать вывод об усилении или уменьшении степени дифференциации точек в торговой сети по критерию фондоотдачи (ФО).

Анализируемые данные представлены в табл. 2.4.

Таблица 2.4

Показатели фондоотдачи торговых точек сети "Океан"

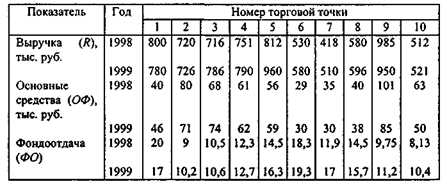
Требуется сравнить показатели фондоотдачи разных предприятий одной торговой сети за отчетный и предыдущий годы. Для того чтобы сделать вывод об усилении или уменьшении степени дифференциации точек торговой сети, можно рассчитать коэффициент вариации фондоотдачи:

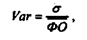
По изменению величины коэффициента вариации можно составить мнение об углублении дифференциации магазинов либо, наоборот, о повышении однородности торговых точек в сети. В частности, наблюдающееся за анализируемые два года уменьшение коэффициента вариации фондоотдачи свидетельствует о повышении однородности различных магазинов сети по этому критерию.

Одной из важнейших аналитических характеристик является степень асимметрии распределения, характеризуемая коэффициентом асимметрии:

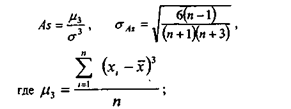
п - количество наблюдений.

Некоторое распределение симметрично в том случае, если As = 0. Чем больше величина As , тем более асимметрично распределение величин.

Крутизна распределения данных характеризуется показателем эксцесса:

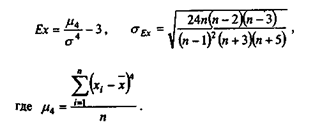
Для нормального распределения Ех = 0. Большой положительный эксцесс означает, что в совокупности данных есть слабо варьирующее по данному признаку "ядро", окруженное редкими, сильно отстоящими от него значениями. Большое отрицательное значение показателя эксцесса говорит об отсутствии такого "ядра".

Расчет всех рассмотренных в данном разделе показателей общности и вариации, характеризующих ряды данных, будет приведен в примере 4.13 (раздел 4.11).

Индексный метод

Мощным орудием сравнительного анализа экономики являются индексы. Индекс - это статистический показатель, представляющий собой отношение двух состояний какого-либо признака. С помощью индексов проводятся сравнения с планом, в динамике, в пространстве. Индекс называется простым (синонимы: частный, индивидуальный), если исследуемый признак берется без учета связи его с другими признаками изучаемых явлений. Простой индекс имеет вид:

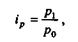
где p₁ и p₀ - сравниваемые состояния признака.

Индекс называется аналитическим (синонимы: общий, агрегатный), если исследуемый признак берется не изолированно, а в связи с другими признаками. Аналитический индекс всегда состоит из двух компонент: индексируемый признак р (тот, динамика которого исследуется) и весовой признак q. С помощью признаков-весов измеряется динамика сложного экономического явления, отдельные элементы которого несоизмеримы. Простые и аналитические индексы дополняют друг друга.

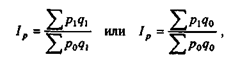
где q₀ или q₁ - весовой признак.

С помощью индексов в анализе финансово-хозяйственной деятельности решаются следующие основные задачи:

оценка изменения уровня явления (или относительного изменения показателя);

выявление роли отдельных факторов в изменении результативного признака;

оценка влияния изменения структуры совокупности на динамику.

Центральной проблемой при построении аналитических индексов является проблема взвешивания. Решая ее, аналитику необходимо сначала выбрать сам весовой признак, а затем - период, на уровне которого берется признак-вес.

Первая из этих задач решается довольно легко путем отыскания системы связанных признаков, произведение которых дает экономически понятный показатель (например, Т = Ч ∙ В из примера 2.2). Что касается второй задачи, то научного обоснования выбора периода весов не существует, в каждом конкретном случае аналитик делает это исходя из задач анализа. Индексы, взвешенные на базовые (q₀) или отчетные (q₁) значения, имеют разный вид и по-разному могут интерпретироваться.

Признак, непосредственно относящийся к изучаемому явлению и характеризующий его количественную сторону, называется первичным или количественным. Первичные признаки объемные, их можно суммировать. Примерами таких признаков являются численность работающих на предприятии (Ч), величина основных средств (ОС) и т.д.

Признаки, относящиеся к изучаемому явлению не непосредственно, а через один или несколько других признаков и характеризующие качественную сторону изучаемого явления, называются вторичными или качественными. Отличительными особенностями вторичных признаков является то, что это всегда относительные показатели, их нельзя непосредственно суммировать в пространстве (исключение — суммирование при расчете некоторых статистик, например, коэффициентов регрессии, корреляции и др., когда экономическая природа показателя не принимается во внимание). В качестве примера можно привести показатели средней заработной платы, рентабельности и т.п.

В анализе выделяют вторичные признаки первого, второго и более высоких порядков. Вторичный признак п-го порядка получается дальнейшей детализацией вторичного признака (n-l)-гo порядка. Связь признаков разных порядков можно проиллюстрировать на примере:

Существует следующее правило определения периода для признака-веса: при построении аналитических индексов по вторичным признакам рекомендуется брать веса на уровне отчетного периода, а по первичным - базисного, т.е.

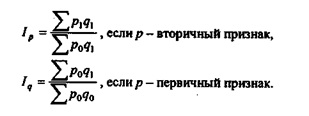
Это обусловлено приоритетностью качественных показателей перед количественными: практический интерес представляет определение экономического эффекта от изменения качественного показателя, полученного в отчетном, а не в базисном периоде. Именно этот подход закладывается при реализации метода цепных подстановок в двухфакторных мультипликативных моделях (в многофакторных моделях привлекается еще и понятие вторичности n-го порядка).

Рассмотрим основные моменты, используемые при решении разного рода задач с помощью индексного метода.