Традиционные методы экономической статистики
Метод средних величин
В любой совокупности экономических явлений или субъектов наблюдаются различия между отдельными единицами этой совокупности. Одновременно с этими различиями существует и нечто общее, что объединяет совокупность и позволяет отнести все рассматриваемые субъекты и явления к одному классу. Например, все рабочие одного цеха, выполняющие одну и ту же работу, выполняют ее по-разному, с разной производительностью. Однако, несмотря на некоторые индивидуальные различия, можно определить среднюю выработку или среднюю производительность на одного рабочего по цеху. Можно усреднить рентабельность предприятия за несколько последовательных кварталов, получив величину средней рентабельности, и т.п.
Роль средних величин, таким образом, заключается в обобщении, т.е. замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности. Например, средний товарооборот на одного работающего является типической характеристикой торговой сети города.
Разумеется, средняя величина не фиксирована раз и навсегда: средняя выработка на одного сотрудника нормально функционирующего предприятия постоянно растет. Средние затраты на единицу продукции с ростом объема выпуска обычно падают. Таким образом, не только сами средние значения величин, но и тенденции их изменения можно рассматривать в качестве индикаторов положения предприятия на рынке и успешности его финансово-хозяйственной деятельности в данной отрасли.
Существует несколько видов средних величин. Наиболее простой и прозрачный смысл имеет средняя арифметическая.
Средняя арифметическая величина - это такое среднее значение признака, при вычислении которого общий объем признака в совокупности не меняется. Иными словами, средняя арифметическая - это среднее слагаемое, при расчете которого общий объем признака в совокупности распределяется поровну между всеми единицами. Например, средняя заработная плата - это такая величина заработной платы, которая приходилась бы на одного работника, если бы весь фонд заработной платы предприятия распределялся между всеми сотрудниками поровну. Формула для расчета средней арифметической:
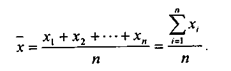
Так вычисляют среднюю величину, если известны все индивидуальные значения в совокупности. Если же объем совокупности велик и представляет собой ряд распределения, используют значение средневзвешенной арифметической средней. Формулу ее расчета и использование в анализе деятельности предприятия иллюстрирует пример 2.5.
Пример 2.5.Молокозавод выпускает сметану различной жирности, реализуя ее по разной цене. Данные о реализации разных сортов сметаны за неделю представлены в таблице.
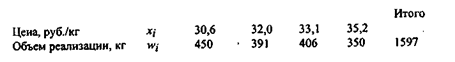
Средняя цена за килограмм сметаны должна представлять собой результат распределения общей выручки от продажи всех сортов по всем 1597 килограммам реализованной продукции. Исчисляется эта величина следующим образом:
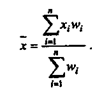
В нашем случае расчет показывает, что средневзвешенная средняя арифметическая цена одного килограмма сметаны, реализованной молокозаводом за анализируемую неделю, составила:
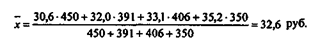
У средней арифметической величины есть ряд свойств, о которых следует помнить аналитику. Эти свойства таковы.
Во-первых, сумма отклонений индивидуальных значений признаков от его среднего значения равна нулю, т.е.:
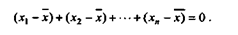
Данное свойство характерно и для средневзвешенных величин.
Во-вторых, если каждое индивидуальное значение признака умножить или разделить на какое-либо число, то и средняя увеличится или уменьшится во столько же раз, т.е.:
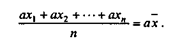
В-третьих, если к каждому значению признака прибавить (или от него отнять) какое-либо число, то средняя увеличится (или уменьшится) на такое же число, т.е.:
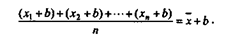
Это свойство иногда применяют при оперировании показателями с большими значениями. Проиллюстрируем сказанное на примере 2.6.
Пример 2.6.Рассчитать средний квартальный объем реализации продукции предприятием по данным за четыре квартала 1998 г.

Из каждого значения xi можно вычесть 587 612, а затем рассчитать среднюю по "остаткам":

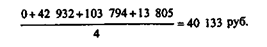
Искомая средняя величина квартальной реализации будет равна
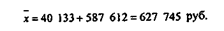
В-четвертых, если веса средней взвешенной умножить или разделить на одно и то же число, величина средней не изменится, т.е.:
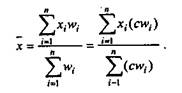
В-пятых, сумма квадратов отклонений индивидуальных значений признака от средней арифметической величины меньше, чем от любого другого числа. На этом свойстве основано применение метода наименьших квадратов, который используется для определения вида регрессионной зависимости между факторами.
Помимо средней арифметической используются и другие формы средних величин. В первую очередь это средняя геометрическая, которая позволяет сохранять неизменным не сумму, а произведение индивидуальных значений величины:
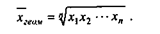
Основное применение средняя геометрическая находит при изучении темпов роста. Рассмотрим ее использование на примере 2.7.
Пример 2.7.Темпы роста цен на сырье, используемое в производстве продукции предприятия, в течение четырех кварталов 1998 г. были различными. Требуется найти квартальный темп роста цен в среднем за год по данным за четыре квартала года.
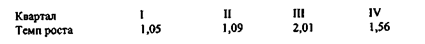
Темп роста цен за год составил: 1,05 ∙ 1,09 ∙ 2,01 ∙ 1,56 = 3,59 .
Если воспользоваться для расчета среднего темпа роста формулой средней арифметической, получим, что ежегодный темп роста составил в среднем 1,43 раза:
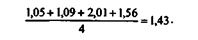
Полученное значение вряд ли дает достоверную картину темпов роста, поскольку если предположить, что цены каждый квартал увеличивались в 1,43 раза, то тогда темп роста за год должен составить 4,15 раза:
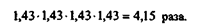
Для того чтобы указанное противоречие не возникало, для расчета среднего квартального темпа роста цен за год следует использовать формулу средней геометрической:
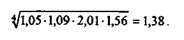
Средняя геометрическая дает наиболее правильный по содержанию результат и в тех случаях, когда требуется найти такое значение экономической величины, которое было бы качественно равноудалено как от ее максимального, так и от минимального значения. Проиллюстрируем это на примере 2.8.
Пример 2.8.В период наибольшей активности рентабельность деятельности гостиницы, расположенной на курорте, составляет 60% в месяц, в периоды ежегодного спада (в так называемый "мертвый" сезон) - 2%. Какова среднемесячная рентабельность работы этого предприятия?
Расчет среднеарифметической величины в данном случае (предполагая, что высокая рентабельность имеет место ровно половину года, а другую половину - низкая) дает результат:
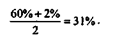
Такая рентабельность - тоже очень высокий показатель. Это значение качественно ближе к 60%, т.е. к максимуму, чем к 2%, т.е. к минимуму. Такой финансовый результат - свидетельство высокой рентабельности, он резко отличается от понятия "низкая рентабельность". Поэтому для расчета величины, которая будет "качественно средней" характеристикой рентабельности, следует использовать формулу среднегеометрической:
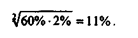
Еще один показатель, характеризующий средние величины, - средняя гармоническая. Он используется в случаях, когда необходимо, чтобы при усреднении оставалась неизменной сумма величин, обратных индивидуальным значениям признака. Формула расчета средней гармонической такова:
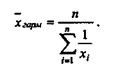
Использование средней гармонической величины иллюстрирует пример 2.9.
Пример 2.9.Рабочий изготавливает на станке 520 деталей за дневную смену. В ночную смену его выработка составляет 450 деталей. Какова среднесменная выработка на одного рабочего, если дневная и ночная смены равны по продолжительности?
При расчете среднесменной выработки необходимо учесть, что продолжительность обеих смен одинакова и равна t. Тогда:
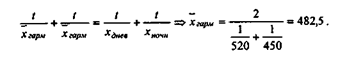
Между приведенными видами средних величин существует следующее соотношение:
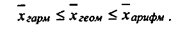
В анализе финансово-хозяйственной деятельности широко используется также средняя хронологическая. Для характеристики предприятия применяются интервальные и моментные показатели. Примерами первых являются товарооборот, прибыль, объем поступления за некоторый период; примерами вторых - данные о запасах, основных средствах, численности работающих на определенную дату. Для усреднения интервальных показателей чаще всего используется формула средней арифметической, а для усреднения моментных показателей как раз и применяется формула средней хронологической.
Если дан ряд моментных показателей: x1, ... , хп, то средняя хронологическая Sch, для этого ряда рассчитывается по формуле:
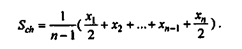
Пример 2.10. Требуется найти величину среднего товарного запаса в магазине в 1999 г., если имеются следующие данные о запасах на начало каждого квартала (тыс. руб.):
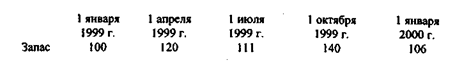
Пользуясь формулой средней хронологической, находим:
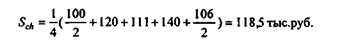
Экономическая интерпретация полученной величины такова: в течение 1999 г. ежедневно предприятие имело запас товаров, равный в среднем 118,5 тыс. руб.
Подчеркнем, что полученное значение средней хронологической является условным - оно дает представление о порядке, а не о точном значении величины запаса, поскольку фактический запас в течение анализируемого периода может ощутимо варьировать. В частности, если бы в распоряжении аналитика (в примере 2.10) имелись данные о запасах на начало каждого месяца или недели, рассчитанное значение среднего запаса почти наверняка было бы другим.
Метод группировки данных
Группировка - это расчленение совокупности данных на группы с целью изучения ее структуры или взаимосвязей между компонентами. В процессе группировки единицы совокупности распределяются по группам в соответствии со следующим принципом: различие между единицами, отнесенными к одной группе, должно быть меньше, чем различие между единицами, отнесенными к разным группам.
Важнейший вопрос при проведении такого рода исследования - выбор интервала группировки. Существуют два основных подхода (метода) к его решению.
Первый подход предполагает деление совокупности данных на группы с равными интервалами значений. Этот метод используется наиболее часто, так как он лишен субъективизма при выборе границ интервалов. При определении длины интервала i целесообразно пользоваться формулами Стерджеса:
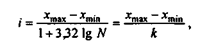
где хmах - максимальное значение признака в изучаемой совокупности;
xmin - минимальное значение признака в изучаемой совокупности;
k - число групп;
N - число наблюдений.
Совершенно очевидно, что знаменатель дроби численно равен количеству групп или интервалов, на которое разбивается исходная совокупность.
Таким образом, оптимальное количество групп, соответствующее некоторому числу наблюдений, согласно формуле Стерджеса можно представить следующим образом:
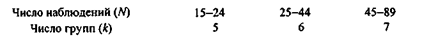
Прямое применение формулы Стерджеса означает, что на параметры группировки не накладывается каких-либо ограничений. Возможен и вариант, когда такие ограничения вводятся, - например, аналитик уже имеет некоторое представление о числе групп (в частности, такое ограничение может быть вызвано желанием обеспечить некоторую качественную однородность выделяемых групп единиц совокупности). В последнем случае длина интервала группировки находится делением размаха вариации, т.е. разности между максимальным и минимальным значениями группировочного признака, на предполагаемое число групп.
Согласно второму подходу интервалы группировки можно выбрать и неравными (возрастающими или убывающими). Этот подход обычно применяется при большой вариации и неравномерности распределения признака по всему интервалу его изменения. При выборе размера интервала группировки руководствуются здравым смыслом и логикой, опираясь при этом на распределения прошлых периодов и традиционно сложившиеся подходы в группировке. При использовании этого подхода интервалы часто выбирают таким образом, чтобы группы были равнозаполненными.
Иллюстрация использования обоих подходов к группировке приведена в примере 2.11.
Пример 2.11. Компания "Фарма" владеет сетью стационарных аптек, аптечных киосков и фармацевтических отделов в различных магазинах города. Выручка 35 торговых точек, принадлежащих компании, за июль 1999 г. составила (тыс. руб.):
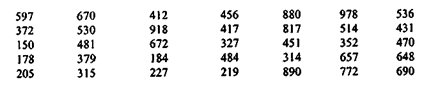
Используя формулу Стерджеса, получим:
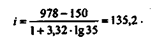
Округлив этот результат, в качестве длины интервала группировки выберем 140. Группировка будет иметь вид:
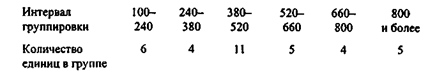
Группировка, по мнению аналитика, получилась не слишком удачная, поскольку не вполне отражает реальную структуру совокупности. Из опыта известно, что все торговые точки, принадлежащие компании "Фарма", можно условно разделить на четыре типа: киоски на улицах, киоски в магазинах, отделы в магазинах и стационарные аптеки. Исходя из представления о том, что совокупность объектов следует разделить на четыре группы, интервал группировки можно определить следующим образом:
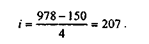
Округлив, возьмем длину интервала группировки равной 200. Тогда группировка примет вид:
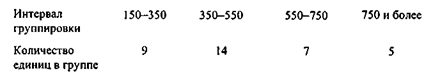
Эта группировка уже гораздо лучше соответствует истинному положению вещей.
Попытка применить подход равнозаполненных интервалов разной длины никакой содержательной информации для анализа в данном случае не даст. Формально такая группировка могла бы выглядеть следующим образом:
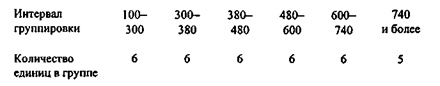
В этой группировке интервалы, начиная со второго, постоянно увеличиваются.
Как отмечалось выше, метод неравных интервалов достаточно обоснован в случае ощутимой вариации группировочного признака. В этом случае применение формулы Стерджеса, предполагающей определенную равномерность в распределении значений группировочного признака внутри интервала варьирования, не дает логически приемлемых результатов. При построении неравных интервалов необходимо ориентироваться на фактическое распределение анализируемой совокупности и пытаться обеспечить достаточную наполненность всех интервалов группировки. Нахождение интервалов может осуществляться методом последовательных итераций.
В некоторых ситуациях при группировке совокупности с ощутимо варьирующим признаком все же возможно применение формулы Стерджеса. Представим себе ситуацию, когда торговая фирма имеет 100 магазинов торговой площадью, варьирующей от 10 до 400 кв. м, и два крупных универмага торговой площадью соответственно 8000 и 12 000 кв. м. Если воспользоваться формулой Стерджеса, получим:
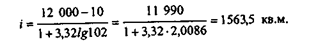
Вся совокупность, следовательно, должна быть разделена на восемь групп, например, следующего вида:

Вряд ли такая группировка представляет интерес для аналитика, поскольку подавляющая часть единиц совокупности попала в один интервал, а большинство других интервалов вообще оказались незаполненными. Поэтому с очевидностью напрашивается вывод о необходимости обособления крупных универмагов в отдельную группу и группировке оставшихся 100 магазинов. Если в этом случае воспользоваться формулой Стерджеса, получим:
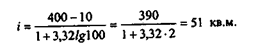
В этом случае совокупность рекомендуется разбить на девять интервалов: в первых восьми интервалах (в соответствии с формулой Стерджеса) будет распределена основная масса магазинов (100), в последний интервал войдут крупные универмаги. Один из вариантов группировки в этом случае может иметь следующий вид:

В общем случае процесс группировки данных включает несколько этапов:
выбор группировочного признака;
упорядочивание совокупности по этому признаку;
определение (тем или иным способом) количества групп;
определение границ интервалов (обычно производится округление формально полученных данных).
Основное правило при проведении группировки состоит в следующем: не должно быть пустых или малозаполненных интервалов. Иными словами, формула Стерджеса дает лишь ориентировочные значения интервалов группировки; при принятии окончательного решения, как правило, значения округляются или незначительно меняются.
В анализе финансово-хозяйственной деятельности используются в основном два вида группировок: структурные и аналитические.
Структурные группировки предназначены для изучения структуры и состава совокупности, происходящих в ней сдвигов относительно выбранного варьирующего признака. Структурная группировка оформляется, как правило, в виде таблицы, в подлежащем которой находится группировочный признак, а в сказуемом - показатели, характеризующие структуру совокупности либо в динамике, либо в пространстве. Этот вид группировки характеризует структуру совокупности по какому-то одному признаку (в примере 2.11 таким признаком является объем выручки торговых точек). Изменение структуры группировки чаще всего описывается одним из двух показателей.
Показатель среднего абсолютного изменения структуры рассчитывается по формуле:
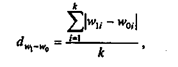
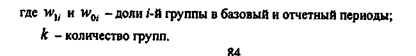
Показатель среднеквадратического изменения структуры рассчитывается по формуле:
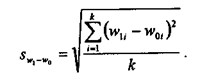
Чем более значительны структурные сдвиги, тем больше значения этих показателей. При отсутствии структурных сдвигов оба они равны нулю. Квадратичный коэффициент реагирует на изменение структуры чуть более чутко. При расчете этих показателей следует помнить о том, что количество групп в группировке и в базовом, и в отчетном периодах должно быть одинаковым.
Аналитические группировки предназначены для изучения взаимосвязей между двумя и более показателями, характеризующими исследуемую совокупность. Один из показателей при этом рассматривается как результативный, а остальные - как факторные. По аналитической группировке можно рассчитать силу связи между факторами.
При оформлении результатов группировки в таблице признак-результат размещается в сказуемом, группировочные признаки, рассматриваемые в качестве факторных, размещаются в подлежащем таблицы.
Выбрать один признак в качестве группировочного зачастую бывает достаточно трудно. Анализ по нескольким признакам довольно трудоемок и обладает принципиальным недостатком - размыванием совокупности, поскольку даже комбинация двух признаков при попытке разбить совокупность на три или четыре категории дает шесть или восемь подгрупп. В некоторых из них оказывается одно-два наблюдения, что недостаточно для подготовки обоснованных выводов об этих подгруппах. Избежать этого недостатка позволяют методы многомерных группировок. Широкое распространение они получили благодаря использованию вычислительной техники при расчетах. При анализе деятельности отдельных предприятий методы многомерной группировки используют нечасто из-за их сложности, более распространены они при социологических и экономических исследованиях отраслей и регионов. Наиболее разработанным методом многомерной классификации является кластерный анализ (см. раздел 2.8.3).
