Оценка эффективности финансовых операций

Показателем, выступающем в качестве меры эффективности вложений средств при различных условиях, является эквивалентная (эффективная) годовая ставка простых или сложных процентов ( ).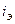

Общий принцип определения эффективности (рентабельности):

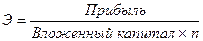(1.54.)

где n – срок, в течение которого эта прибыль получена. Применительно к депозитам и депозитным операциям прибылью будет сумма начисленных процентов ( 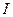), вложенным капиталом – первоначальная сумма вклада ( 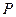), а сроком, в течение которого эта прибыль получена – период наращения ( ).

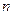Нетрудно доказать, что эффективная ставка простых процентов будет равна ставке простых процентов

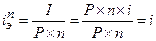(1.55.)

При определении доходности краткосрочных (до года) вкладов эффективная ставка простых процентов может быть определена также по формуле:

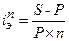(1.56.)

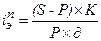(1.57.)

Если известна ставка простых процентов на периоде начисления - 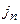, то эффективная годовая ставка простых процентов определяется по формуле:

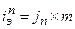(1.58.)

При начислении процентов один раз в конце года эффективная ставка сложных процентов определяется по формуле:

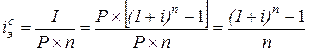(1.59.)

При начислении процентов р - раз в году формула может иметь следующий вид:

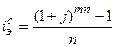(1.60.)

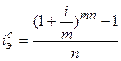(1.61.)

При этом, если 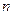= 1, то формула принимает вид:

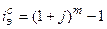(1.62.)

При определении реальной доходности вкладных операций следует учитывать налогообложение. С учётом налога доход вкладчика (сумма процентов) составит:

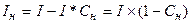(1.63.)

где 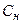- ставка налога на доход в долях единицы.

Реальная доходность в виде эффективной годовой ставки процентов при этом будет равна:

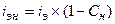(1.64.)

Расчеты в условиях инфляции

Инфляция характеризуется обесцениванием национальной валюты и общим повышением уровня цен внутри страны. Измеряются темпы инфляции с помощью индексов цен, которые выражаются обычно в процентах и определяются по формуле:

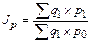(1.65.)

где 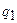- количество товаров, включённых в потребительскую корзину в анализируемом периоде;

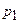- цены соответствующих товаров в анализируемом периоде;

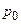- цены этих же товаров в базовом периоде.

Названия определенных уровней инфляции

Индекс инфляции, %	Название
	Низкая
	Ползучая
	Галопирующая
	Гиперинфляция
	Суперинфляция

В долях единицы индекс инфляции 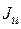показывает, во сколько раз выросли цены за рассматриваемый период.

Уровень инфляции 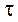(в %) показывает на сколько процентов выросли цены за рассматриваемый период времени:

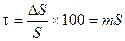% (1.66.)

где 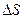- сумма, на которую надо увеличить первоначальную сумму 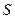для сохранения её покупательной способности в будущем.

Взаимосвязь между уровнем и индексом инфляции за один и тот же период выражается формулой (во всех формулах ниже 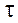и ):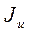

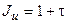(1.67.)

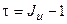(1.68.)

Индекс инфляции за период, состоящий из 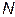-го количества более коротких периодов, характеризующихся своим уровнем инфляции, можно определить по формуле:

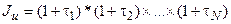(1.69.)

где 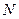- количество интервалов в наблюдаемом периоде.

При равных интервалах и равных уровнях инфляции за каждый интервал формула принимает вид:

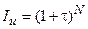(1.70.)

Будущую сумму, покупательная способность которой с учётом инфляции будет равна покупательной способности первоначальной суммы 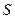, можно определить по формулам:

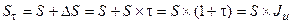(1.71.)

Будущую сумму 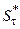,характеризующую реальное, обесцененное в результате инфляции значение нынешней суммы 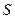, можно определить по формуле:

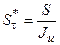(1.72.)

Следовательно, реальную покупательную способность наращенной суммы, обесцененной в результате действия инфляции можно определить следующим образом:

а) для ставки простых процентов:

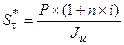(1.73.)

б) для ставки сложных процентов при их начислении один раз в конце года:

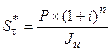(1.74.)

в) при начислении сложных процентов несколько раз в году:

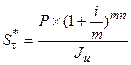(1.75.)