Алгебраическое решение модели Вильяма Баумола

1. Оптимальная сумма одного займа: ,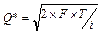

где Т –планируемая потребность в ДС;

F – фиксированные затраты по одной сделке (расходы по конвертации денежных средств в ценные бумаги;

i – процентная ставка рыночных ценных бумаг за период (или приемлемый для предприятия % доход по вложениям в ценные бумаги) .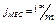

2. Количество займов: .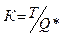

3. Средний остаток ДС: 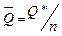. n=2

Пример

Потребность предприятия в денежных средствах составляет 4 млн руб в месяц. Эта потребность может покрываться краткосрочными займами равномерно в течение месяца. Определить оптимальную сумму одного займа, их количество в месяц, если расходы по оформлению каждой сделки составляет 100 руб. Номинальная ставка 6% годовых.

Решение

Оптимальная сумма 1 займа определяется по формуле:

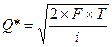
F – общая потребность в денежных средствах за период;

T - расходы по оформлению одной сделки

j_мес - процентная ставка за период (месяц)

j_мес.= i / m =6% / 12= 0,5%

_____________________

Q* =√ (2×4×10⁶ ×100) / 0.0005 =400000 руб

Количество займов в течение месяца: К=F/Q =10 займов

Средний остаток денежных средств: Q= Q* / 2 =200000 руб.

Алгебраическое решение модели Миллера-Орра

Реализация модели осуществляется в несколько этапов:

1. Экспертно определяется минимальная величина ДС на р/с (Q_min).

2. На основе статистических данных определяется вариация ежедневного поступления ДС на р/с (σ²) (σ-среднеквадратичное отклонение).

3. Определяются потери («упущенная выгода»), связанные с хранением денежных средств на р/счете - (j). Обычно в размере ежедневной ставки % по краткосрочным ценным бумагам.

4. Определяются расходы по конвертации денег в ценные бумаги (и наоборот). Расходы принимают в размере ставки комиссионных (f).

5. Определяют размах вариации остатка денежных средств на р/счете (Z): .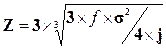

6. Рассчитывают верхнюю границу остатка денежных средств на р/счете: .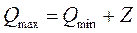

7. Определяется точка возврата (Qтв), т.е. величина среднего остатка денежных средств : .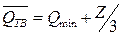

Если страховой запас равен нулю, то точка возврата определяется: .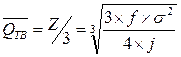

Когда остаток денежных средств достигает max значения (верхней границы), излишние денежные средства (по отношению к точке возврата) инвестируются в краткосрочные финансовые инструменты. При достижении min значения (нижней границы), пополнение денежных средств до уровня точки возврата осуществляется за счёт продажи части краткосрочных финансовых инструментов.

Пример. Определить параметры модели Миллера-Орра оптимизирующие остаток свободных денежных средств предприятия исходя из следующих данных.

Параметры модели Миллера-Орра.

1. Принимаем экспертно заданную, исходя из сложившейся практики, величину остатка денежных средств на р/счете Q_min =10 000 $.

2. Среднеквадратичное отклонение потока денежных средств σ=2000$.

Следовательно - вариация ежедневного потока денежных средств

_δ² = 2000² = 4×10⁶ $

3. Годовая ставка доходности по ценным бумагам i_год = 11,6%

Необходимо определить ставку процентов за установленный период - 1 день

j Þ (1+ j)365 =1,116 , Þ j = 365√ 1,116 -1 = 0,0003 Þ j = 0,03%

4. Расходы по конвертации денежных средств в ценные бумаги (и обратно) составляют фиксированную величину f = 25$

5. Определяем размах вариации остатка денежных средств на р/счете 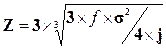Z = 3 ³√3×25×4×10⁶/4×0,0003 =18900$

6. Определяем верхнюю границу остатка денежных средств

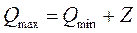Q_max =10000 + 18900 = 28900 $

7. Определяем точку возврата, т.е. величину среднего остатка денежных средств 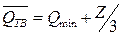. Q_тв = 10000 + 18900×1/3 =16300 $

Пояснения. Модель работает следующим образом. При достижении уровня 28900$ - верхней границы остатка денежных средств на сумму 12600$ (28900 – 16300) покупаем ценные бумаги, при этом остаток денежных средств на расчетном счете составит 16300$ - уровень точки возврата. . При достижении уровня 10000$ - нижней границы остатка на сумму 6 300$ (16300 – 10000) продаем ценные бумаги, при этом остаток денежных средств на р/счете снова достигнет уровня точки возврата - 16 300$.