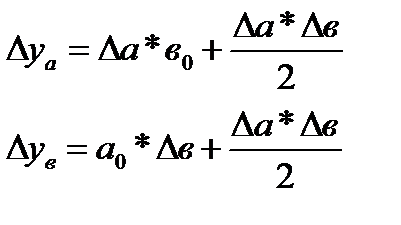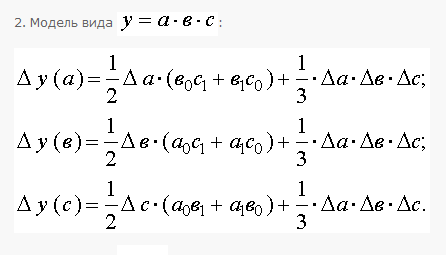Основные свойства детерминированного подхода к анализу. Типы детерминированных моделей: аддитивные, мультипликативные, кратные, смешанные.

Факторный анализ – это анализ влияния отдельных факторов на изменение результативного показателя с помощью детерминированных или стохастических приемов исследования.

Детерминированный факторный анализ – это методика исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

Стохастический анализ направлен на изучение косвенных связей, т.е. опосредованных факторов.

Стохастический анализ выступает в качестве инструмента углубления детерминированного анализа факторов, по которым нельзя построить детерминированную модель.

Классический метод стохастического моделирования – корреляционно-регрессионный анализ. Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями.

Основные свойства детерминированного подхода к анализу:

- построение детерминированной модели путем логического анализа;

- наличие полной (жесткой) связи между показателями;

- невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;

- изучение взаимосвязей в краткосрочном периоде.

Различают четыре типа детерминированных моделей:

1) аддитивные модели у = а + в + с

2) мультипликативные модели у = а*в*с

3) кратные модели у = а/в

4) смешанные модели у = (а + в)/с

2. Приемы преобразования факторных моделей с целью включения новых факторов: удлинения, расширения и сокращения.

Для детализации обобщающего факторного показателя на его составляющие используют прием удлинения факторной системы.

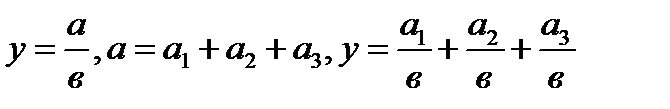
Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей

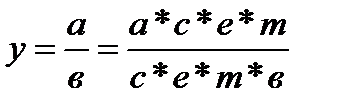
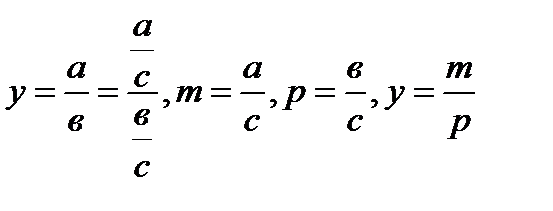Для построения новых факторных показателей применяют прием сокращения факторных моделей

3. Способы оценки влияния факторов: цепных подстановок, абсолютных разниц, относительных разниц, интегральный, индексный.

Принципы построения модели:

- место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;

- модель должны строить из полной двухфакторной модели путем последовательного расчленения факторов, как правило, качественных, на составляющие;

- при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.

Способы оценки влияния факторов:

Цепных подстановок

Абсолютных разниц

Относительных разниц

Интегральный

Способ цепных подстановок

1. Рассчитываются базисное, промежуточные и фактическое значения результативного показателя.

y0 = a0 ´ b0 ´ c0;

ya = a1 ´ b0 ´ c0;

yb = a1 ´ b1 ´ c0;

y1 = a1 ´ b1 ´ c1

a0, b0, c0 - базисные значения факторов, оказывающих влияние на обобщающий показатель у;

a1, b1, c1 - фактические значения факторов;

ya, yb - промежуточные изменения результирующего показателя, связанного с изменением факторов а, b соответственно.

Общее изменение Δ у = у1 - у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

Δ у = Δ уa + Δ уb + Δ уc;

Δ уa = уa - у0;

Δ уb = уb - уa;

Δ уc = у1 - уb.

Способ абсолютных разниц

Способ абсолютных разниц является модификацией способа цепной подстановки.

Изменение результативного показателя за счет каждого фактора определяется как произведение отклонения изучаемого фактора на базисное или отчетное значение другого фактора в зависимости от выбранной последовательности подстановки:

y0 = a0 ´ b0 ´ c0;

Δуa = Δa ´ b0 ´ c0;

Δуb = a1´ Δb ´ c0;

Δуc = a1 ´ b1´Δc ;

Δу = Δуa + Δуb +Δуc.

Способ относительных разниц

Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.

1. Находят относительное отклонение каждого факторного показателя:

Δа%, Δв%, Δс%.

2. Определяют отклонение результативного показателя уза счет каждого фактора:

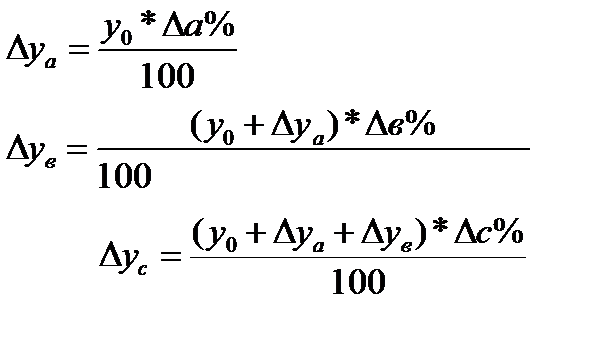
Интегральный метод

Интегральный метод позволяет избежать недостатков, присущих методу цепной подстановки.

Операция вычисления определенного интеграла осуществляется с помощью вычислительных возможностей персональных компьютеров.

Можно использовать также уже сформированные рабочие формулы, приводимые в специальной литературе:

Модель вида y = a ´ b: