Основные шаги решения проблем оценки проекта

Трудность оценки инвестиционного проекта возникает в первую очередь из-за того, что потоки денежных средств "уходят" и "приходят" в разное время. Как уже было сказано, типичным инвестиционным профилем явля­ется разовая крупная "утечка" денежных средств, а затем периодические относительно меньшие "вливания" в течение нескольких лет.

Можно условно разделить весь период реализации инвестиционного периода на следующие этапы:

• период 0 — сегодня;

• период 1 — один год спустя после начала реализации проекта;

• период 2 — два года спустя;
и т. д.

Хорошо известно, что деньги, которые имеются сегодня, дороже той же номинальной суммы, но полученной в будущем, через какое-то время. Это явление получило название "стоимость денег во времени" (time value of money). В связи с этим нельзя просто сравнивать сегодняшние деньги и будущие поступления непосредственно.

Поэтому требуется иметь механизм, который позволяет выразить стои­мость потоков денежных средств в один определенный момент времени. Чаще всего выбирается в качестве такого момента период 0.

Этот подход показан на рис. 16.2. В этом случае каждый будущий поток денежных средств трансформируется так, чтобы получить его "приведен­ную стоимость" (present value), т. е. его стоимость на период 0. Для этого применяется так называемый фактор дисконтирования* (discount factor). Способы расчета рассматриваются в следующем параграфе.

После того как получены приведенные стоимости всех потоков денежных средств, их уже можно сравнивать между собой напрямую, так как они представлены в стандартизованном виде, т. е. приведенном к единому ос­нованию. Если суммировать их, то получается общая приведенная стои-

В отечественных изданиях используются также термины "текущая стоимость", "сегодняшняя стои­мость" по отношению к понятию present value и коэффициент, или множитель, дисконтирования как синоним "фактора дисконтирования". — Прим. научн. ред.

Глава 16. ИНВЕСТИЦИОННЫЕ ПОКАЗАТЕЛИ 255

Часть V. ПРИНЯТИЕ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

мость всех будущих потоков денежных средств, которые поступят от ана­лизируемого проекта. В свою очередь эту величину теперь можно срав­нить непосредственно с первоначальными вложениями и на основании этого сделать вывод о целесообразности реализации рассматриваемого проекта или отказе от него.

Фактор дисконтирования

Как было уже сказано, известно, что денежные средства, которые должны поступить в будущем, имеют меньшую стоимость, чем сегодняшние де­нежные средства в таком же количестве. Но насколько меньше?

Можно отыскать ответ на поставленный вопрос, если задать сначала дру­гой, промежуточный: "Если бы у меня было 100 долл., которые я мог бы положить на банковский депозит под 10% годовых, сколько денег я полу­чил бы через год?" Ответ очень прост — 110 долл.

Следовательно, приведенная стоимость будущих ПО долл. (будущее в этом случае наступит через 1 год) при процентной ставке в 10% (0,1 при выражении ее в десятичном виде) равняется 100 сегодняшних долларов. Таким образом, можно получить приведенную стоимость будущих денеж­ных средств, используя для этого специальный фактор, связанный с дан­ной процентной ставкой. В рассматриваемом примере мы разделили будущие денежные средства на выражение, равное (1 + процентная ставка в десятичном виде), т. е. ПО долл. / (1 + 0,1) ⁼ 100 долл. (Математиче­ски тождественно получить тот же результат, если умножить будущие денежные средства на фактор дисконтирования, обратный величине 1,1, т. е. 0,909= 1/1,1.) Если будущие потоки денежных средств поступят и во второй период, т. е. период 2, то проделанную выше операцию надо повторить. На практике, однако, можно этого не делать, а воспользо­ваться фактором дисконтирования, который позволяет получить тот же результат.

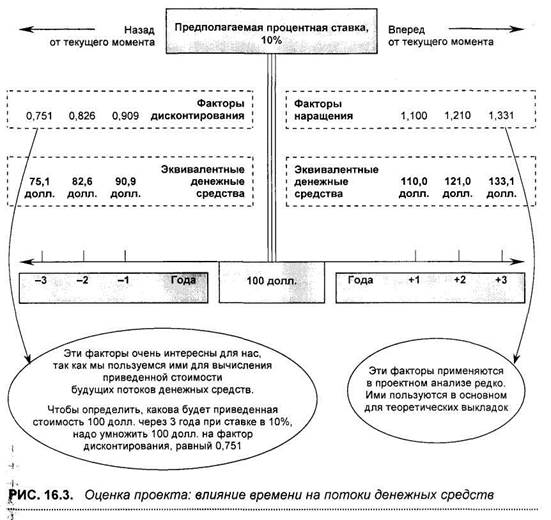
На рис. 16.3 показан эффект, который возникает, если необходимо пере­считать сегодняшние денежные средства в будущие или, наоборот, в прошлые.

В центре рисунка помещен блок, в котором указаны первоначальные 100 долл., которые по определению сразу же относятся к периоду 0. Пе­риоды, относящиеся к будущему и к прошлому, показаны соответственно справа и слева от этого блока. Для упрощения будем считать, что про­центная ставка не меняется и равна 10%. Если будем двигаться вправо от центрального блока, фактор наращения в зависимости от периода равен: 1,100; 1,210; 1,331 и т. д., что соответственно означает расчеты для перио­дов 1, 2, 3 и т. д. методом сложного процента (с учетом накопления или реинвестирования прироста в каждом периоде. — Прим. научн. ред.).

Если, например, нам нужно вычислить, какие денежные средства через 3 года будут иметь приведенную стоимость в 100 долл., нужно 100 долл. умножить на фактор наращения для периода 3, т. е. 1,331. В результате получим, что приведенную стоимость в 100 долл. имеют будущие (через 3 года) денежные средства в размере 133,1 долл.

Влево от центрального блока показаны соответствующие факторы дис­контирования для прошлых лет, соответственно 0,909; 0,826; 0,751 и т. д. Если, например, воспользоваться последним из них, то легко можно под­считать, что стоимость в 100 долл. сейчас соответствует 75,1 долл. приве­денной стоимости.

В оценке инвестиционных проектов используется фактор дисконтирова­ния, который на схеме 16.3 расположен слева от центрального блока.

Часть V. ПРИНЯТИЕ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

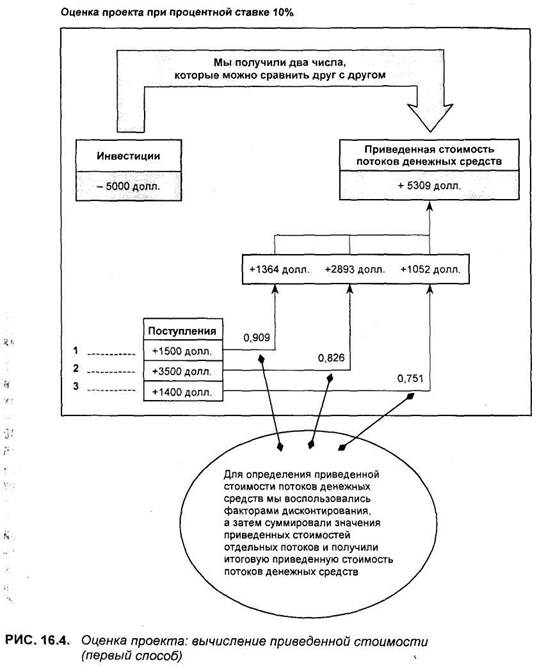
Чтобы провести анализ, сначала необходимо выбрать соответствующую процентную ставку. При более высокой процентной ставке фактор дис­контирования будет ниже, и наоборот. (В приложении 4 дана таблица фак­торов дисконтирования и факторов наращения.) Пользуясь этой таблицей, можно вычислить приведенную и, наоборот, будущую (наращенную) стоимость любых денежных средств на любой момент времени как в про­шлом, так и в будущем.