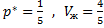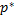Правило минимизации среднего ожидаемого риска.

Риск фирмыпри реализации i-го решения является случайной величиной 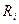с рядом распределения 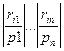. Математическое ожиданиеи есть средний ожидаемый риск, обозначаемый также 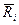. Правило рекомендует принять решение, влекущее минимальный

средний ожидаемый риск.

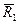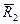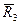Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем = 20/6, = 4, = 7/6 , 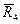= 32/6 . Минимальный средний ожидаемый риск равен 7/6 и соответствует третьему решению.

Замечание.Отличие частичной (вероятностной) неопределенности от полной неопределенности очень существенно. Конечно, принятые по правилам Вальда, Сэвиджа, Гурвица решения никто не считает окончательными, самыми лучшими. Это только лишь

первый шаг, некоторые предварительные соображения. Далее пытаются узнать что-то о вариантах реальной ситуации, в первую очередь о возможности того или иного варианта, о его вероятности. Но когда мы начинаем оценивать вероятность варианта, это уже

предполагает повторяемость рассматриваемой схемы принятия решений: это уже было в прошлом, или это будет в будущем, или это повторяется где-то в пространстве, например, в филиалах фирмы.

Метод создания интегрального показателя для учета риска

Суть метода

Для нахождения интегрального показателя рассматривается конечная последовательность факторов в количестве n штук. Значение этих факторов будем рассматривать как координаты вектора в n-мерном пространстве.

Далее рассматриваем n-весов – значимости каждого из факторов, которые задаются экспертно, т.е. определяется вектор из n-значений.

Интегральным показателем признается скалярное произведение этих 2-х векторов.

Примечание.Чем больше интегральный показатель, тем больше преимуществ у данного решения.

Парето

Итак, при попытке выбрать наилучшее решение мы столкнулись с тем, что каждое решение имеет две характеристики — средний ожидаемый доход и средний ожидаемый

риск. Теперь имеем оптимизационную двухкритериальную задачу по выбору наилучшего решения.

Существует несколько способов постановки таких оптимизационных задач.

Рассмотрим такую задачу в общем виде. Пусть А — некоторое множество операций, каждая операция а имеет две числовые характеристики Е(а), r(а) (эффективность и риск, например) и разные операции обязательно различаются хотя бы одной характеристикой. При выборе наилучшей операции желательно, чтобы Е было больше, а r меньше. Будем говорить, что операция а доминирует операцию b, и обозначать а 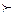b, если Е(а) 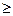Е{b) и r(a) 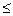r(b) и хотя бы одно из этих неравенств строгое. При этом операция а называется

доминирующей, а операция b — доминируемой. Ясно, что ни при каком разумном выборе наилучшей операции, доминируемая операция не может быть признана таковой. Следовательно, наилучшую операцию надо искать среди недоминируемых операций.

Множество этих операций называется множеством Парето или множеством оптимальности по Парето.

Теория конфликтов

Виды конфликтов

- Антагонистический – конфликт, в котором выигрыш одной стороны – есть проигрыш другой. Обычно рассматриваются 2 стороны конфликта, такой конфликт называется игрой.

- Неантагонистический – конфликт, характеризующийся тем, что в игре могут принимать участие несколько игроков, причем у каждого свой набор стратегий и своя функция выигрыша, определенная на пространстве всевозможных исходов. Таким образом, выигрыш одного из игроков может не быть проигрышем другого. При этом вопрос объединения игроков для достижения наибольшего выигрыша в группе игроков не рассматривается.

- Коалиционные – подобные конфликты не являются антагонистическими, основной задачей является создание такой коалиции игроков и такого распределения выигрыша, при котором каждый из участников получает максимально возможный выигрыш.

Антагонистические игры

Пример 1.

Простейшим примером антагонистической игры является игра "Орлянка". Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает - он платит первому одну денежную единицу, если угадывает - первый платит ему одну денежную единицу.

В данной игре каждый участник имеет две стратегии: "орел" и "решка". Множество ситуаций в игре состоит из четырех элементов. В строках таблицы указаны стратегии первого игрока х, в столбцах - стратегии второго игрока y. Для каждой из ситуаций указаны выигрыши первого и второго игроков.

X Y	Орел	Решка
Орел	-1, 1	1, -1
Решка	1, -1	-1, 1

В аналитическом виде функция выигрыша первого игрока имеет следующую форму:

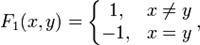
где x 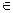X и y 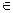Y - стратегии первого и второго игроков, соответственно.

Так как выигрыш первого игрока равен проигрышу второго, то 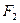(x,y) = − 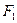(x,y).

Неантагонистические игры

Пример.

Задача про мужа и жену.

Муж: 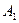- футбол Жена: 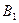- футбол

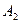- теща 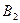- мама

Функция выигрыша:

МужаЖены

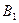
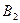
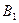
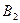
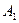
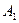
Принципы оптимальности

Оптимальность по Парето.

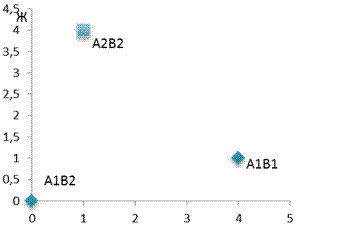
Пример 1 (муж и жена):

М

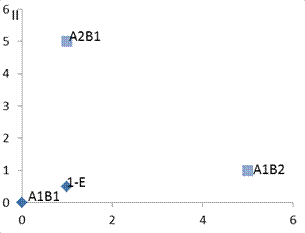
Пример 2 (автомобили):

Равновесие по Нэшу.

Пример (муж и жена):

Анализ ситуации А1В1 по Нэшу жена: переход к В2 уменьшит выигрыш, это не выгодно. Муж: переход к А2 уменьшит выигрыш с 4 до 0, это не выгодно, следовательно такая ситуация будет равновесно по Нэшу. Ситуация А1В2,А2В1 не равновесны по Нэшу. А2В2 равновесные.

6.3. Анализ оптимальности по Парето и по Нэшу на примерах.

Муж и жена. Автомобили

ПО РН	_ _
_ _	ПО НР

_ _	ПО НР
ПО НР	_ _

Множество альтернатив (4), попробуем выяснить, не сможем ли мы получить лучшее, в каком- либо отношении решение, если будем выбирать стратегии, как это делается в антагонистической игре (например, к чему приводит применение смешанных стратегий).

м/ж	В1	В2
А1
А2

P ‾ вероятность частоты выбора А1

Средний выигрыш мужа при условии выбора стратегии В1

1-p

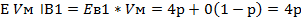
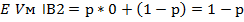
Выберем то самое р, при котором средний выигрыш мужа оказывается max:

4р=1-р

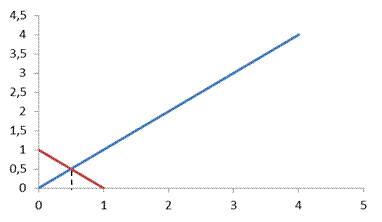
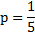
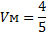
Аналогично: выигрыш жены