Метод оценки денежных потоков, основанный на учете фактора времени

Фактор времени занимает важнейшее место в финансовых вычислениях; деньги имеют такую объективно существующую характеристику, как временную ценность:

· получение денег сегодня дает нам возможность заработать проценты на эти деньги завтра, поэтому сумма, полученная сегодня, больше той же суммы, полученной завтра;

· денежная наличность обесценивается за определенный период времени в связи с инфляцией.

Отсюда вытекают два важных следствия:

а) необходимость учета фактора времени при проведении долгосрочных финансовых операций;

б) некорректность с точки зрения долгосрочных финансовых операций суммирования денежных величин, относящихся к разным периодам времени.

Чтобы сопоставлять денежные суммы, поступившие в разное время, не­обходимо привести их к одному моменту времени.

Для этого используются опе­рации дисконтирования и наращения (компаундирования или капитализации).

Дисконтирование — приведение разновременных денежных потоков к началь­ному моменту.

Наращение — приведение разновременных денежных потоков к будущему моменту времени.

Операции дисконтирования и наращения осущест­вляются с учетом возможности альтернативного вклада с отдачей в виде перио­дических процентных выплат.

Процентная выплата (ссудный процент) — доход в денежной форме, получаемый кре­дитором за пользование его денежными средствами.

Процентная ставка (или ссудный процент) — относи­тельный процентный доход, выраженный в процентах годовых от номинала. Про­центные выплаты могут начисляться различными способами.

Практическое использование получили две схемы начисления процентов: про­стого и сложного процента.

Схема простого процента — начисление процентной выплаты без учета накопленного дохода (без учета реинвестирования процентных выплат).

Схема сложного процента — начисление процентной выплаты с учетом накопленного дохода (с учетом реинвестирования процентных выплат).

Каждый год приносит проценты в сумме = PV•r.

Следовательно, на весь срок проценты (I) составят:I= PV•r•n

Наращенная сумма (будущая стоимость) находится следующим образом:

FV= PV + I = PV + PV•r•n = PV (1+r•n ),

где FV — будущая стоимость; PV — текущая стоимость; r - процентная ставка, измеренная в долях единицы; n — срок финансовой операции (или время начисления процентных платежей), обычно измеряется в годах.

Это выражение называется формулой наращения по простым процентам. Множитель (1+r•n) – множителем наращения по простым процентам.

Как правило, процентная ставка устанавливается на год, так что при сроке операции менее года необходимо определить, какая часть годового процента уплачивается кредитору. Для этого срок операции представляется в виде частного:

n = t: Т,

где t - число дней ссуды; Т – число дней в году.

Используя данные обозначения, можно записать формулу определения наращенной (будущей стоимости):

FV= PV (1+r )

При расчетах применяются две временные базы:

1) 360 дней — тогда получают обыкновенные (коммерческие) про­центы;

2) 365 (366) дней — точные проценты.

Модель генерирования денежных потоков сложными процен­тами.

В среднесрочных и долгосрочных операциях, если проценты не выплачиваются после их начисления, а присоединяются к первоначаль­ной сумме для наращения, как правило, применяют сложные процен­ты. База для начисления не остается постоянной, а увеличивается с каждым периодом.

Присоединение начисленных процентов к базовой сумме для на­числения процентов называется капитализацией процентов.

Формула расчета наращенной суммы при условии, что проценты начисляются и капитализируются один раз в год, имеет следующий вид:

FV = PV(l+r)ⁿ.

Величину (l+r)ⁿ называют множителем наращения по сложным процентам.

Для удобства использования расчетные значения данного множителя, называемого мультиплицирующим множителем FM1 (г, п), табулированы для различных значений г и я, которые отражены в финансовых таблицах:

FM1 (i;n) = (l +г)ⁿ

(В современных условиях проценты капитализируются обычно не один, а несколько раз в течение года (по полугодиям, кварталам, меся­цам, дням). При начислении процентов несколько раз в год пользуют­ся модифицированной формулой, в которой начисление происходит по ставке , количество периодов начисления составляет п • т.

Наращенная сумма в данном случае находится по формуле:

FV= PV (1+r ) ^nm

m — количество начислений процентов в течение одного года.

Для сравнения финансовых операций с различной частотой на­числения и неодинаковыми процентными ставками применяется эффективная процентная ставка.

Эффективная процентная ставка ( j) — это реальный относительный доход, который получают в целом за год от начисления процентов несколько раз в течение года. Это ставка сложных процентов, которая дает тот же результат, чтл и m-разовое начисление процентов по ставке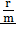

По определению множители по двум ставкам должны быть равны друг другу, т.е.:

(1+ j)ⁿ= (1+r ) ^nm

Отсюда эффективная ставка равна:

j= (1+ ) ^m - 1

Как видно, при m>1®r, при m=1® j = r не изменяет финансовых обязательств, то говорят, что ставки эквиваленты.

Аналогично наращению осуществляется процедура дисконтирования. Она представляет собой обратный процесс, т.е. приведение будущих потоков к текущему периоду с учетом изменения стоимости денег с течением времени.