Кудрявцева И.Ю., Почекаева О.В.

«Методы финансовых вычислений в учете и анализе»: учебно-методическое пособие для студ.очного и заочного факультета экономики и управления по направлению 080100 «Экономика» (квалификация (степень) «Бакалавр») /, И.Ю. Кудрявцева, О.В. Почекаева - Н.Новгород: Изд-во ФБОУ ВПО «ВГАВТ», 2014. – с.69

Учебно-методическое пособие по курсу «Методы финансовых вычислений в учете и анализе» предназначено для студентов очного и заочного обучения факультета экономики и управления ВГАВТа по направлению подготовки 080100 «Экономика» (квалификация (степень) «Бакалавр». В нем излагаются методические рекомендации по выполнению самостоятельных заданий.

Ответственный редактор – профессор, к.э.н., зав. кафедрой учета, анализа и аудита ВГАВТ Сивоволов Н.В.

Учебно - методическое пособие обсуждено и одобрено на заседании кафедры учета, анализа и аудита ВГАВТа __________

ã ФБОУ ВПО «ВГАВТ», 2014

Введение

Финансовые вычисления появились с возникновением товарно-денежных отношений и являются одной из основных базовых составляющих коммерческого дела.

В отдельную отрасль знания финансовые вычисления оформились только в XIX в: они назывались "коммерческие вычисления" или "коммерческая арифметика". Как утверждал русский математик, финансист и бухгалтер Н.С. Лунский, коммерческая математика изначально существовала под именем "политической арифметики", родоначальником которой является английский экономист Вильям Петти, – отец политической экономии и родоначальник статистической науки.

Быстрый экономический рост стран в XIX в. во многом был обусловлен распространением коммерческих знаний. В частности, в России действия правительства привели к тому, что к концу XIX в. появились коммерческие училища, торговые школы, классы, курсы, поскольку актуальность и важность коммерческого образования не у кого не вызывала сомнения, а основу коммерческих наук составляла коммерческая арифметика, так как именно она обуславливает каждый торговый акт, каждую финансовую операцию.

В послереволюционный период коммерческая арифметика в России не получила должного развития, поскольку многие вопросы, связанные с финансами и финансовыми расчетами, попросту игнорировались. В странах с ориентацией на рыночную экономику коммерческая арифметика развилась в самостоятельное направление в науке – в финансовую математику.

Российская экономика все более интегрируется в мировую экономику, что требует использования финансового инструментария, применяемого развитыми странами и международными организациями в финансовой практике.

Становление рыночных отношений в России сопровождается появлением навыков и методов, которыми приходится овладевать для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и др.

Кардинальное изменение банковской системы, внедрение новых форм собственности, развитие фондового рынка и финансовой самостоятельности предприятий сделали актуальным управление финансовыми ресурсами, одним из краеугольных элементов которого являются финансовые вычисления, базирующиеся на понятии временной ценности денег.

В этих условиях обоснованность принимаемых управленческих решений (а многие из них по сути своей имеют финансовую природу) в значительной степени определяется качеством финансово-аналитических расчетов.

При подготовке экономистов, финансистов, бухгалтеров, коммерсантов, менеджеров и маркетологов большое внимание уделяется изучению теории и практики финансово-экономических расчетов, необходимых в анализе инвестиционных проектов, расчете кредитных и коммерческих операций, эффективности предпринимательской деятельности, в страховом деле.

Тема 1. Простые ставки

Простые процентные ставки

Процесс движения денежных потоков от настоящего к будущему – называется наращением.

Процесс движения денежных средств от будущего к настоящему – дисконтированием.

При наращении определяется будущая стоимость денежных средств, при дисконтировании – текущая (сегодняшняя, дисконтированная) стоимость. При расчете будущей и текущей стоимости используется понятие процента.

Процент – плата, взимаемая за заем некоторой суммы денег.

На практике при проведении финансовых расчетов могут использоваться разные способы начисления процентов и разные виды ставок.

Сложные ставки (dc)

Процентная ставка – плата, выраженная как процент от общей суммы, кредитуемой на определенный период, обычно на год.

Учетная ставка — финансовый термин, финансовая категория, употребляемая для характеристики следующих процессов, связанных с кредитованием:

1. Под учётной ставкой понимается процентная ставка, по которой Банк России предоставляет кредиты коммерческим банкам. В российской практике наряду с термином учётная ставка для данной ситуации применяется термин ставка рефинансирования.

2. Под учётной ставкой понимается процент, курс, взимаемый банком с суммы векселя при «учёте векселя» (покупке его банком до наступления срока платежа). Фактически, учётная ставка в данном случае — это цена, взимаемая за приобретение обязательства до наступления срока уплаты. При учёте Банком России государственных ценных бумаг или предоставлении кредита под их залог применяется термин официальная учётная ставка.

В свою очередь и процентные и учетные ставки подразделяются на простые и сложные.

Существуют два способа начисления процентов:

1) декурсивный способ начисления (процентная ставка). Проценты начисляются в конце каждого интервала начисления.

2) антисипативный (предварительный) способ начисления -проценты начисляются в начальный момент времени, поэтому заемщик получает на руки сумму за вычетом процентных денег.

Процентная ставка характеризует доходность кредитной сделки. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Величина процентной ставки определяется отношением:

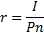(1.1)

где r - процентная ставка;

I - величина дохода владельца капитала;

Р – сумма капитала предоставляемого в кредит;

n – срок ссуды в годах.

Величина процентного дохода определяется по формулам:

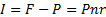(1.2)

Где F – наращенная сумма.

Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) запишется в следующем виде:

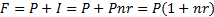(1.3)

При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражают дробным числом:

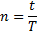(1.4)

где t – число дней функционирования сделки( число дней на которое предоставлен кредит);

Т – временная база (число дней в году).

Формула наращенной суммы с использованием простых процентов примет вид:

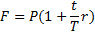(1.5)

Различают три метода процентных расчетов, которые зависят от выбранного периода начисления:

1. Точные проценты с точным числом дней ссуды (английская практика). Продолжительность года принимается равной 365 (366) дней, а продолжительность месяцев – в днях, также соответствующих календарному исчислению, т.е. 28,29,30,31 день.

Точное число дней ссуды определяется по специальным таблицам как разность порядкового номера дня окончания ссуды и порядкового номера дня выдачи ссуды.

2. Обыкновенные проценты с точным числом дней ссуды (французская практика). Продолжительность года принимается , равной 360 дней, а продолжительность месяца соответствует календарному исчислению.

3.Обыкновенные проценты с приближенным числом дней ссуды (германская практика). Продолжительность года принимается равной 360 дней, продолжительность месяцев по 30 дней в каждом, начиная с момента выдачи ссуды и до момента ее погашения, и точным числом дней ссуды в неполном месяце.

При использовании Германской и Французской практики день выдачи и день погашения ссуды считается за один день.

Простые учетные ставки

Наряду с декурсивным методом существует и другой способ начисления процентов. Суть его сводится к тому, что проценты начисляются в начале расчетного периода, при этом базу (100%) принимается сумма погашения долга. В этом случае применяется не процентная ставка (r), а учетная ставка (d). Такой метод начисления процентов носит название антисипативный (предварительный). При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (то есть наращенной суммы). Эта сумма и считается величиной получаемого кредита (ссуды). Т.к. проценты в данном случае начисляются в начале каждого интервала начисления, заемщик получает сумму кредита за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке или коммерческим (банковским) учетом.

Дисконт – это доход, полученный по учетной ставке, то есть разница между размером предоставляемого кредита и непосредственно выдаваемой ссудой.

Введем обозначения:d - годовая учетная ставка; Р - сумма, получаемая заемщиком; F – сумма подлежащая возврату.

Для расчета показателей используемых при предоставлении кредита используются формулы:

1. Для определения суммы, получаемой заемщиком :

а) в конце первого интервала:

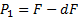(1.6)

б) в конце второго интервала:

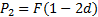(1.7)

в) на весь период кредитования

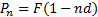(1.8)

2. Для определения наращенной суммы:

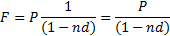(1.9)

3. Для определения суммы, получаемой заемщиком при периоде начисления, не равным году:

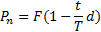(1.10)

4. Для определения наращенной суммы при периоде начисления не равном году:

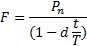(1.11)

5. Для определения наращенной суммы при использовании разных ставок на разных интервалах начисления:

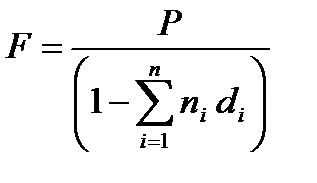(1.12)