Для случайного повторного отбора (для средней)
Задача. С вероятностью 0,9973 определить в каких пределах находится средний срок изделий в генеральной совокупности ( 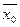 ), если отобрано 250 деталей, из которых средний срок службы 41,9 месяца (
), если отобрано 250 деталей, из которых средний срок службы 41,9 месяца ( 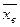 ) и среднеквадратическое отклонение
) и среднеквадратическое отклонение 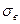 = 6,2 месяца.
= 6,2 месяца.
Дано:
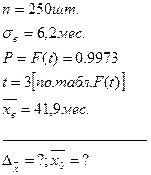 [25]
[25]
Решение:
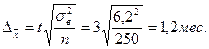
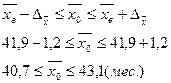
Вывод: С вероятностью 0,9973 можно утверждать, что средний срок службы изделий в генеральной совокупности находится в пределах от 40,7 до 43,1 месяца.
Для случайного повторного отбора (для доли)
Задача. С вероятностью 0,9973 определить в каких пределах находится в генеральной совокупности доля изделий срок службы которых превышает 50 месяцев, если доля изделий, срок службы которых превышает 50 месяцев в выборочной совокупности равна 0,124, отобрано 250 изделий.
Дано:
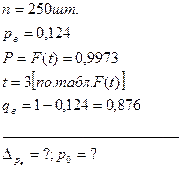
Решение:
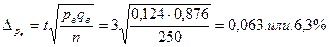
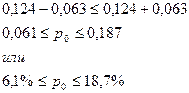
Вывод: С вероятностью 0,9973 можно утверждать, что доля деталей в генеральной совокупности срок службы которых превышает 50 месяцев составляет не менее 6,1% и не более 18,7%.
Таблица 18
Предельная ошибка выборки и объем выборки при различных видах отбора
| Виды отбора | Повторный | Бесповторный | ||||
 | t дисперсия средняя | n объем выборки |  | t дисперсия средняя | n объем выборки | |
| Случайный отбор 1. Для средней | 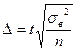 n – объем выборки t – стандартное отклонение n – объем выборки t – стандартное отклонение 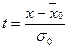 | 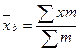 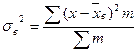 | 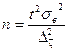 | 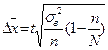 | 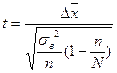 | 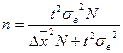 |
| 2. Для доли | 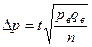 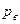 - частность выборочная - частность выборочная 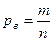 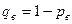 | –- | 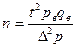 | 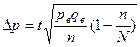 | 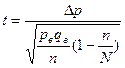 | 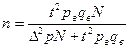 |
| Механический отбор | Формулы случайного бесповторного отбора | |||||
| Типический отбор 1. Для средней | 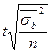 n – объем выборки n – объем выборки 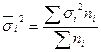 | 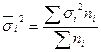 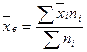 i – тип явления i – тип явления | 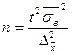 | 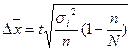 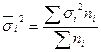 | 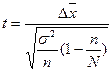 | 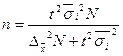 |
| 2. Для доли | 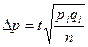 | средняя доля 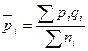 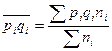 n – выборочное n – выборочное | 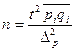 | 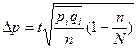 | 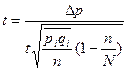 | 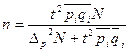 |
Для случайного повторного отбора (для средней)
Задача. При испытании на крепость отобраны в случайном порядке 400 отрезков пряжи одиночной нити (основа – 65 кордная) были получены следующие результаты[26]:
Таблица 19
Расчет основных выборочных характеристик ( 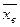 и
и 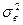 ).
).
Крепость пряжи (гр.) 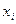 | Число испытанных образцов m | 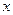 (середина интервала) (середина интервала) | 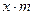 | 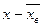 | 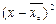 | 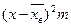 |
| A | 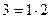 | 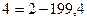 | 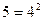 | 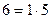 | ||
| 105-125 | -84,4 | 7123,36 | 56986,88 | |||
| 125-145 | -64,4 | 4147,36 | 99536,64 | |||
| 145-165 | -44,4 | 1971,36 | 78854,4 | |||
| 165-185 | -24,4 | 595,36 | 21432,96 | |||
| 185-205 | -4,4 | 19,36 | 2013,44 | |||
| 205-225 | 15,6 | 243,36 | 29203,2 | |||
| 225-245 | 35,6 | 1267,36 | 44357,6 | |||
| 245-265 | 55,6 | 3091,36 | 61827,2 | |||
| 265-285 | 75,6 | 5715,36 | 40007,52 | |||
| 285-305 | 95,6 | 9139,36 | 54836,16 | |||
| Итого | 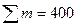 | 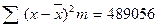 |
Определите с вероятностью 0,97 среднюю крепость пряжи во всей партии.
Для определения основных характеристик ( 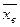 и
и 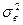 ) выборочной совокупности необходимо найти графы с 3-ей по 6-ую в таблице 19.
) выборочной совокупности необходимо найти графы с 3-ей по 6-ую в таблице 19.
Выборочная средняя крепость пряжи равна:
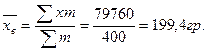
Выборочная дисперсия составляет:
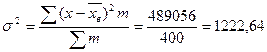
Итак, на основе следующих данных определим среднюю крепость пряжи во всей партии.
Дано:
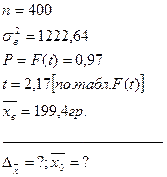 [27]
[27]
Решение:
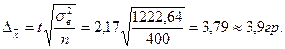
Тогда средняя крепость пряжи во всей партии будет находиться в следующих пределах:
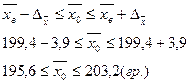
Вывод: С вероятностью 0,97 можно утверждать, что средняя крепость во всей пряжи в генеральной совокупности будет не менее 195,6 гр. и не более 203,2 гр.
Доля случайного повторного отбора (для доли)
Задача. По данным предыдущей задачи с вероятностью 0,97 найти доля образцов пряжи во всей партии с крепостью выше 185 гр.
Дано:
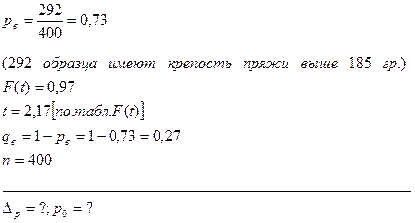 [28]
[28]
Решение:
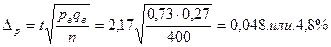 доля образцов пряжи во всей партии с крепостью.
доля образцов пряжи во всей партии с крепостью.
Вывод: С вероятностью 0,97 можно утверждать, что доля образцов во всей партии в генеральной совокупности с крепостью выше 185 гр. находятся в пределах 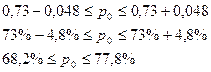 .
.
2-ой тип задач – Определение вероятности того, что предельная ошибка выборки не превышает заданной величины.
Случайный повторный отбор
Задача. С какой вероятностью можно утверждать, что выборочная доля бракованных деталей будет отличатся от генеральной доли не более чем на 1%, если при измерении 115 деталей установлена доля брака равная 0,5%?
Дано:
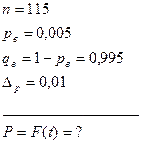
Решение:
Знаем, что:
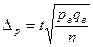
тогда 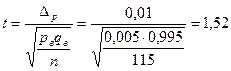 , а вероятность
, а вероятность 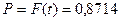 (по таблице F(t))[29]
(по таблице F(t))[29]
Вывод: С вероятностью 0,8714 можно утверждать, что выборочная доля бракованных деталей будет отличаться от генеральной доли не более чем на 1%.
3-ий тип задач – Определение минимального объема выборки
