Собственно-случайная выборка

Случайным отбором называется такой отбор, при котором единицы из генеральной совокупности отбираются наудачу, по жребию. При этом каждая единица совокупности обладает одинаковой объективной возможностью быть отобранной. Таким образом, в отобранной части могут быть представлены единицы от всех частей генеральной совокупности, со всеми признаками, которые имеются у единиц генеральной совокупности. При таком отборе в средней выборочной 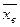значения изучаемого признака будут представлены достаточно точно и, как принято говорить, выборочная совокупность будет репрезентативна генеральной совокупности то есть обобщающие характеристики выборочной совокупности будут близки к соответствующим характеристикам генеральной совокупности.

Но случайный отбор не следует понимать как беспорядочный отбор. Производя отбор, необходимо обеспечить соблюдение принципа случайности, организовать отбор так, чтобы его ошибки были действительно случайными.

Случайный отбор может быть повторным и бесповторным.

Механическая выборка

При механическом отборе единицы для обследования отбираются уже не наудачу. При этой форме выборочного наблюдения единицы генеральной совокупности располагаются в каком-то порядке, но только не по изучаемому признаку, а, скажем, в алфавитном. Затем упорядоченная известным образом исходная совокупность делится на определенное число равных частей, и из каждой такой части отбирается одна единица – представитель с определенным порядковым номером (10-я, 20-я, 30-я). Например, при 10% выборке из совокупности в 1000 единиц она должна быть разделена на 100 равных частей, из которых могут быть отобраны 5-я, 15-я, 25-я и т.д. единицы.

5-я	15-я	25-я	…	985-я	995-я
			…980

Могут быть взяты и другие порядковые номера.

Таким образом, если при случайном отборе есть лишь возможность попадания в выборку единиц от всех частей генеральной совокупности, то механический отбор направлен на то, чтобы обеспечить попадание в выборку таких представителей. В этом смысле, механический отбор можно назвать направленным отбором, и поэтому, при правильной организации, он репрезентативнее случайного отбора.

Математическая статистика не располагает специальными зависимости для расчета средней ошибки выборки при механическом отборе, и она вычисляется по той же формуле, что и в условиях случайного бесповторного отбора. Следовательно, величина вычисленной таким образом средней ошибка механического отбора оказывается несколько завышенной.

Типическая выборка

Типический отбор также принадлежат к числу направленных видов отбора. При типическом отборе совокупность также разделяется на части, но не механически, а по каком-то типическому признаку. Например, для обследования бюджетов рабочих все рабочие данного предприятия предварительно группируются по профессиям, т.е. по признаку, который определяет уровень заработной платы. Затем из каждой группы производят случайный или механический отбор. При типическом отборе обеспечивается попадание в выборку представителей всех типических групп, что повышает репрезентативность выборочных данных.

Типичные группы могут быть как равными, так и не равными по численности. В последнем случае отбор производится пропорционально объему каждого типа во всей генеральной совокупности. Типический отбор бывает повторным и бесповторным.

Серийная (гнездовая) выборка

Серийный (гнездовой) отбор заключается в том, что отбору подвергается совокупность не отдельных единиц, а серий или групп их. При этом внутри групп обследуются все единицы, без исключения. В сельскохозяйственной статистике, где отбираемые серии хозяйств называют «гнездами», этот вид отбора получил название гнездового.

Отбор серий может быть организован как случайный, так и механический. Серийный отбор бывает повторный и бесповторный.

Рассмотрим основные типы задач согласно задачам выборочного метода[24].

Случайный отбор

1-ый тип задач – Определение предельной ошибки выборки.