Сформулируйте теоремы о перемещениях плоской фигуры. Сделайте соответствующие рисунки
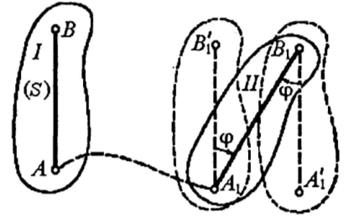 Т1: Всякое перемещение плоской фигуры в её плоскости можно осуществлять посредством поступательного перемещения вместе с произвольной точкой (полюсом) и вращением вокруг этого полюса.
Т1: Всякое перемещение плоской фигуры в её плоскости можно осуществлять посредством поступательного перемещения вместе с произвольной точкой (полюсом) и вращением вокруг этого полюса.
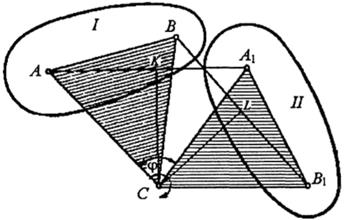 Т2 (Эйлера-Шаля): Всякое непоступательное перемещение плоской фигуры в её плоскости может быть осуществлено посредством одного вращения вокруг некоторого центра, называемого центром конечного вращения.
Т2 (Эйлера-Шаля): Всякое непоступательное перемещение плоской фигуры в её плоскости может быть осуществлено посредством одного вращения вокруг некоторого центра, называемого центром конечного вращения.
23. 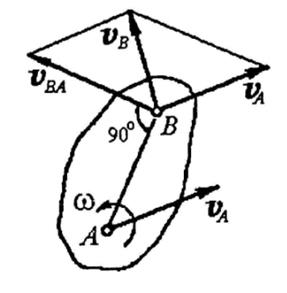 Запишите формулу распределения скоростей точек плоской фигуры. Как определить скорость точки плоской фигуры с помощью формулы? Сделайте соответствующий рисунок.
Запишите формулу распределения скоростей точек плоской фигуры. Как определить скорость точки плоской фигуры с помощью формулы? Сделайте соответствующий рисунок.
Скорость 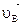 любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости
любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости 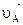 другой, произвольно выбранной и принятой за полюс, точки А и скорости
другой, произвольно выбранной и принятой за полюс, точки А и скорости 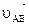 точки В в ее вращении вместе с плоской фигурой вокруг этого полюса.
точки В в ее вращении вместе с плоской фигурой вокруг этого полюса.
24.  Что называется мгновенным центром скоростей? Как определить положение мгновенного цетра скоростей в общем и частных случаях? Сделайте соответствующие рисунки.
Что называется мгновенным центром скоростей? Как определить положение мгновенного цетра скоростей в общем и частных случаях? Сделайте соответствующие рисунки.
- При всяком непоступательном перемещении плоской фигуры существует единственная точка этой фигуры, скорость которой в данный момент равная нулю. Точка Р плоской фигуры, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей.
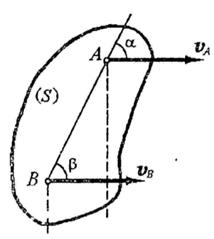
- Для определения положения мгновенного центра скоростей Р надо знать только направления скоростей 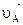 и
и  каких-нибудь двух точек А и В сечения S. Мгновенный центр скоростей находиться в точке пересечения перпендикуляров, восстановленных из точек А и В к скоростям этих точек.
каких-нибудь двух точек А и В сечения S. Мгновенный центр скоростей находиться в точке пересечения перпендикуляров, восстановленных из точек А и В к скоростям этих точек.
 Пусть скорости
Пусть скорости  и
и  любых двух точек А и В параллельны друг другу и при этом линия АВ не перпендикулярна к
любых двух точек А и В параллельны друг другу и при этом линия АВ не перпендикулярна к 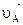 , а следовательно, и к
, а следовательно, и к 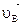 . Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что:
. Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что: 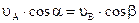 , но
, но 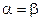 , поэтому
, поэтому 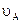 =
= 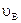 и, следовательно,
и, следовательно, 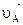 =
= 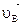 . Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость
. Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость  плоской фигуры в этот момент равна нулю.
плоской фигуры в этот момент равна нулю.
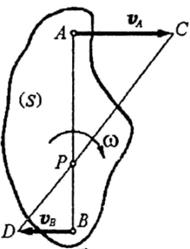
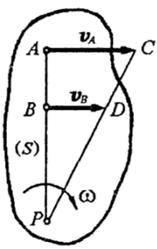
Пусть скорости 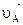 и
и 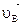 точек А и В параллельны друг другу и эти точки лежат на одном перпендикуляре к данным скоростям. В этом случае при
точек А и В параллельны друг другу и эти точки лежат на одном перпендикуляре к данным скоростям. В этом случае при 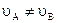 мгновенный центр скоростей Р определяется построениями.
мгновенный центр скоростей Р определяется построениями.
В этом случае для нахождения мгновенного центра скоростей Р нужно, кроме направлений, знать еще и модули скоростей 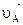 и
и 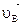 .
.
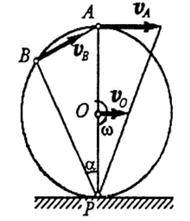
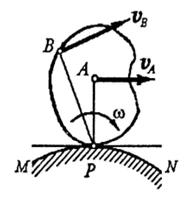 В практических задачах часто приходится иметь дело со случаем, когда плоская фигура катится без скольжения по некоторой неподвижной кривой MN.
В практических задачах часто приходится иметь дело со случаем, когда плоская фигура катится без скольжения по некоторой неподвижной кривой MN.
В этом случае скорость точки касания контура плоской фигуры с кривой MN равна нулю, так как точки касания обоих тел при отсутствии скольжения должны иметь одинаковые скорости, а кривая MN неподвижна. Отсюда следует, что точка касания Р является мгновенным центром скоростей плоской фигуры.
Как определить скорость точки плоской фигуры с помощью мгновенного центра скоростей? Запишите необходимые формулы, пояснив их на рисунке. Каковы будут скорости точек плоской фигуры в том случае, когда мгновенный центр скоростей этой фигуры окажется на бесконечности?
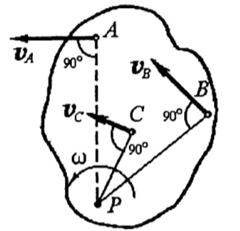 Для определения скорости любой точки тела достаточно знать модуль и направление скорости какой-нибудь одной точки А тела и направление скорости другой его точки В. Тогда, восстановив из точек А и В перпендикуляры к направлениям их скоростей
Для определения скорости любой точки тела достаточно знать модуль и направление скорости какой-нибудь одной точки А тела и направление скорости другой его точки В. Тогда, восстановив из точек А и В перпендикуляры к направлениям их скоростей  и
и 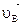 , найдём положение мгновенного центра скоростей Р и по направлению скорости
, найдём положение мгновенного центра скоростей Р и по направлению скорости 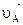 определим направление вращения тела. После этого, зная модуль скорости
определим направление вращения тела. После этого, зная модуль скорости 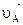 , найдём по формуле
, найдём по формуле 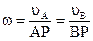 скорость точки В.
скорость точки В.
АР и АВ – мгновенные радиусы вращения.
Модуль угловой скорости тела, как видно из формулы 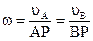 в каждый момент равен отношению модуля скорости какой-нибудь точки сечения S к расстоянию этой точки до мгновенного центра скоростей Р. Кроме того, модуль угловой скорости тела можно определить с помощью формулы:
в каждый момент равен отношению модуля скорости какой-нибудь точки сечения S к расстоянию этой точки до мгновенного центра скоростей Р. Кроме того, модуль угловой скорости тела можно определить с помощью формулы: 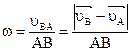
 Пусть скорости
Пусть скорости 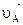 и
и 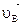 любых двух точек А и В параллельны друг другу и при этом линия АВ не перпендикулярна к
любых двух точек А и В параллельны друг другу и при этом линия АВ не перпендикулярна к 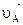 , а следовательно, и к
, а следовательно, и к 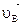 . Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что:
. Из теоремы о проекциях скоростей двух точек на прямую, соединяющую эти точки, следует, что: 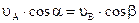 , но
, но 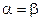 , поэтому
, поэтому 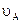 =
= 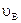 и, следовательно,
и, следовательно, 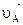 =
= 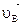 . Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость
. Таким образом, в рассматриваемом случае скорости всех точек плоской фигуры в данный момент равны и по модулю, и по направлению. Такое состояние плоской фигуры называется мгновенно поступательным. Так как перпендикуляры, восстановленные из точек А и В к скоростям этих точек, не пересекаются, то в рассматриваемом случае в данный момент мгновенный центр скоростей находится в бесконечности. Угловая скорость 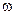 плоской фигуры в этот момент равна нулю.
плоской фигуры в этот момент равна нулю.
Сформулируйте теорему о проекциях скоростей двух точек плоской фигуры. Как определить скорость фигуры с помощью этой теоремы? Запишите необходимую формулу, пояснив её с помощью рисунка.
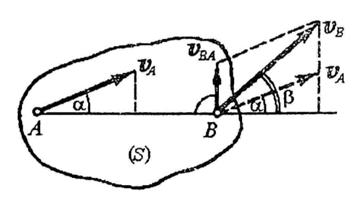 Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.
Проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки, равны между собой.
Предположим что известны модуль и направление скорости точки А и направление скорости точки В. Принимая точку А за полюс, можно записать:
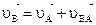
Проецируя обе части этого неравенства на линию АВ и учитывая, что вектор  перпендикулярен к АВ, приходим к результату:
перпендикулярен к АВ, приходим к результату: 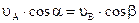 .
.
27. Запишите формулу распределения ускорений плоской фигуры. Как определить ускорение точки плоской фигуры с помощью формулы распределения ускорений? Сделайте соответствующий рисунок.
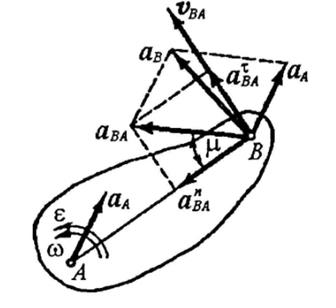 Ускорение любой точки В плоской фигуры в каждый данный момент времени равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в её вращательном движение вместе с полюсом фигурой вокруг этого полюса.
Ускорение любой точки В плоской фигуры в каждый данный момент времени равно геометрической сумме двух ускорений: ускорения произвольного полюса А и ускорения точки В в её вращательном движение вместе с полюсом фигурой вокруг этого полюса.
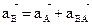 подставив:
подставив: 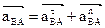 , получим:
, получим: 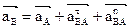 .
.
28.  Какая точка называется мгновенным центром ускорений? Как определить положение МЦУ и как с его помощью определить ускорение любой точки плоской фигуры? Сделайте соответствующий рисунок.
Какая точка называется мгновенным центром ускорений? Как определить положение МЦУ и как с его помощью определить ускорение любой точки плоской фигуры? Сделайте соответствующий рисунок.
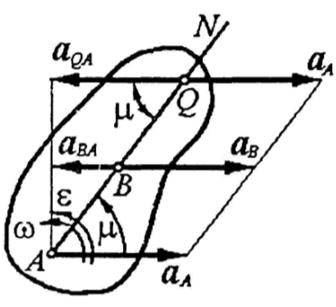
При непоступательном движении плоской фигуры в её плоскости, на фигуре (или на вязанной с ней подвижной плоскостью) в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений.
Если известно ускорение какой-либо точки А плоской фигуры, а также её угловая скорость и угловое ускорение. Тогда положение мгновенного центра ускорений определяется следующим образом:
1. Находим значение угла 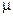 из формулы:
из формулы: 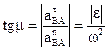 .
.
2. Из точки А, ускорение которой известно, под углом 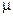 к вектору
к вектору 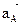 проводим полупрямую AN, которая должна быть отклонена от
проводим полупрямую AN, которая должна быть отклонена от 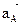 на угол
на угол 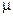 в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, то есть в строну направления углового ускорения
в сторону вращения фигуры, если вращение ускоренное, и против вращения, если оно является замедленным, то есть в строну направления углового ускорения  , показанного на рисунку дуговой стрелкой.
, показанного на рисунку дуговой стрелкой.
3. На полученной полупрямой AN отложим отрезок 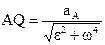 . Конец Q этого отрезка и будет мгновенным центром ускорений.
. Конец Q этого отрезка и будет мгновенным центром ускорений.
Если точку Q выбрать за полюс, то, поскольку  , ускорение любой точки М плоской фигуры, согласно формуле
, ускорение любой точки М плоской фигуры, согласно формуле 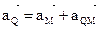 , будет равно ускорению точки М во вращательном движении этой точки вокруг мгновенного центра ускорений, то есть:
, будет равно ускорению точки М во вращательном движении этой точки вокруг мгновенного центра ускорений, то есть: 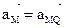 . Модуль ускорения точки М будет равен
. Модуль ускорения точки М будет равен  . Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение было вращательным вокруг мгновенного центра ускорений. При этом выполняются следующие условия:
. Следовательно, ускорения точек плоской фигуры определяются в данный момент времени так, как если бы движение было вращательным вокруг мгновенного центра ускорений. При этом выполняются следующие условия:  .
.
Как формулируется теорема о перемещении твёрдого тела, имеющего одну неподвижную точку? Поясните с помощью рисунка, как направлены векторы угловой скорости и углового ускорения при движении тела в одной неподвижной точкой?
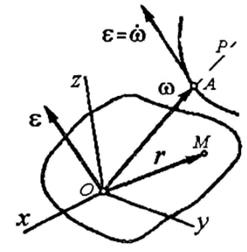 - Произвольное перемещение твердого тела вокруг неподвижной точки можно осуществить одним поворотом вокруг определенным образом выбранной оси, проходящей через эту точку и называемой осью конечного вращения. Мгновенная ось вращения представляет собой геометрическое место точек, скорости которых в данный момент равны нулю.
- Произвольное перемещение твердого тела вокруг неподвижной точки можно осуществить одним поворотом вокруг определенным образом выбранной оси, проходящей через эту точку и называемой осью конечного вращения. Мгновенная ось вращения представляет собой геометрическое место точек, скорости которых в данный момент равны нулю.
- Угловая скорость 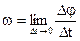 с которой происходит элементарный поворот тела вокруг мгновенной оси вращения, называется мгновенной угловой скоростью. Следует иметь в виду, что
с которой происходит элементарный поворот тела вокруг мгновенной оси вращения, называется мгновенной угловой скоростью. Следует иметь в виду, что 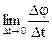 не равен производной от угла
не равен производной от угла 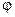 , так как при сферическом движении тела такого угла не существует. Мгновенная угловая скорость
, так как при сферическом движении тела такого угла не существует. Мгновенная угловая скорость 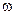 должна быть задана в функции времени непосредственно. Ее можно изобразить вектором
должна быть задана в функции времени непосредственно. Ее можно изобразить вектором 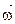 , направленным по мгновенной оси вращения ОР так, чтобы, глядя с конца вектора
, направленным по мгновенной оси вращения ОР так, чтобы, глядя с конца вектора 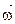 , видеть вращение тела против хода часовой стрелки. При движении тела вектор
, видеть вращение тела против хода часовой стрелки. При движении тела вектор 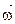 в общем случае изменяется и по величине, и по направлению. Производная от
в общем случае изменяется и по величине, и по направлению. Производная от 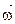 по времени определяет вектор
по времени определяет вектор 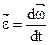 называемый мгновенным угловым ускорением, или угловым ускорением тела в данный момент времени. Направление вектора
называемый мгновенным угловым ускорением, или угловым ускорением тела в данный момент времени. Направление вектора 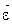 совпадает с направлением касательной к годографу вектора
совпадает с направлением касательной к годографу вектора 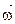 и изображается отложенным от точки О.
и изображается отложенным от точки О.
