Цилиндрические зубчатые передачи
Рассмотрим основные виды этих передач.
1. Рядовой назовем передачу, в которой все оси колес, находящихся в последовательном зацеплении, неподвижны. При этом одно из колес (например, колесо 1 на рис.61) является ведущим, а остальные ведомыми.
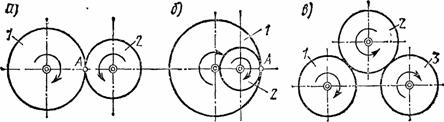
Рис.61
В случае внешнего (рис. 61, а) или внутреннего (рис. 61, б) зацепления двух колес имеем 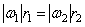 , так как скорость точки сцепления А у обоих колес одинакова. Учитывая, что число z зубцов сцепленных колес пропорционально их радиусам, а вращения колес происходят при внутреннем зацеплении в одну сторону, а при внешнем в разные, получаем
, так как скорость точки сцепления А у обоих колес одинакова. Учитывая, что число z зубцов сцепленных колес пропорционально их радиусам, а вращения колес происходят при внутреннем зацеплении в одну сторону, а при внешнем в разные, получаем
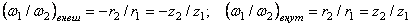 .
.
При внешнем зацеплении трех колес (рис. 61, в) найдем, что
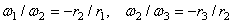 и
и 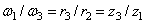 .
.
Следовательно, отношение угловых скоростей крайних шестерен в этой передаче обратно пропорционально их радиусам (числу зубцов) и не зависит от радиусов промежуточных (паразитных) шестерен.
Из полученных результатов следует, что при рядовом сцеплении шестерен
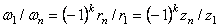 .
.
где k - число внешних зацеплений (в случае, изображенном на рис.61,а имеется одно внешнее зацепление; на рис.61, в - два внешних зацепления, на рис.61, б внешних зацеплений нет).
Передаточным числом данной зубчатой передачи называется величина 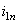 , дающая отношение угловой скорости ведущего колеса к угловой скорости ведомого:
, дающая отношение угловой скорости ведущего колеса к угловой скорости ведомого:
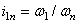 .
.
2. Планетарной называется передача (рис.62), в которой шестерня 1 неподвижна, а оси остальных шестерен, находящихся в последовательном зацеплении, укреплены на кривошипе АВ, вращающемся вокруг оси неподвижной шестерни.
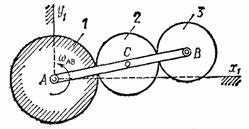
Рис.62
3. Дифференциальной называется передача, изображенная на рис. 62, если в ней шестерня 1 не является неподвижной и может вращаться вокруг своей оси А независимо от кривошипа АВ.
Расчет планетарных и дифференциальных передач можно производить, сообщив мысленно всей неподвижной плоскости Ах1y1 вращение с угловой скоростью - 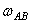 , равной по модулю и противоположной по направлению угловой скорости кривошипа АВ (метод остановки или метод Виллиса).
, равной по модулю и противоположной по направлению угловой скорости кривошипа АВ (метод остановки или метод Виллиса).
Тогда кривошип в этом сложном движении будет неподвижен, а любая шестерня радиуса 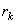 будет иметь угловую скорость
будет иметь угловую скорость
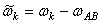 ,
,
где 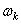 - абсолютная угловая скорость этой шестерни по отношению к осям Ах1y1 (рис.62). При этом оси всех шестерен будут неподвижны и зависимость между
- абсолютная угловая скорость этой шестерни по отношению к осям Ах1y1 (рис.62). При этом оси всех шестерен будут неподвижны и зависимость между 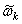 можно будет определить, приравнивая скорости точек сцепления.
можно будет определить, приравнивая скорости точек сцепления.
Расчет планетарных и дифференциальных передач можно также производить с помощью мгновенных центров скоростей.
Вопросы для самопроверки
- Приведите определение абсолютного (сложного) движения точки.
- Абсолютное, относительное, переносное движение точки.
- Какое движение твердого тела называют простым?
- Какие системы координат выбирают при определении скоростей твердых тел при сложном движении?
- Какое движение считают переносным, а какое – относительным?
- Какое движение точки называется относительным и какое переносным?
- Сформулируйте теорему о сложении скоростей.
- Назовите составляющие вектора ускорения при сложном движении точки.
- Как определяются модуль и направление ускорения Кориолиса?
- При каком сложном движении точки ускорение Кориолиса равно нулю?
- Как определяют абсолютную скорость точки в сложном движении?
- Как определяют абсолютное ускорение точки при непоступательном переносном движении и при поступательном переносном движении?
- Каковы причины появления кориолисова ускорения?
- Назвать случаи, когда кориолисово ускорение точки равно нулю.
