Расчет и построение диаграммы управляемости

Для расчета зависимостей, входящих в диаграмму управляемости, первоначально следует определить ряд вспомогательных величин, полученных в результате преобразования уравнений движения к виду, удобному для расчетов. Указанные величины определяются по выражениям :

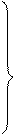a₂ = C₃ – m ' + E æ_r χ = -0,131

b₂ = C₁+ E æ_r = 0,195

a₃ = χ C₆ + χ C₇ β² + E æ_r χ = 0,189 [6]

b₃ = - χ C₅ + E æ_r.= 0,051

здесь С₁ – С₇ – коэффициенты корпусных усилий (для одиночных судов С₇=0);

m ' - безразмерная масса судна;

Е - эффективность ДРК

æ_н – обобщенный коэффициент трансформации потока;

χ - относительное отстояние ДРК от центра тяжести судна ;

χ - величина обратная χ ;

В свою очередь: m' = 2 δ В / L = 2 × 0,71 × 12/80 = 0,213 [8]

χ = L_дрк / L = 40/ 80 = 0,5 [9]

χ = 1 / χ = 1/ 0,5 = 2 [10]

здесь δ – коэффициент полноты водоизмещения;

L _дрк – отстояние ДРК то центра тяжести судна = 67,5 (м).

Далее определяются величины:

Р = (а₃ b₂ - а₂ b₃) / 2 × (С₂а₃ - С₄b₃) [11]

Р = (0,22 × 0,48 – (-0.09)*0.12 ) / 2 ( 0.4*0.22-0) =0.0016

Q = C ₄ E/ 2 (C₂a₃ - C₄b₃) [12]

Q = 0/2(0.4 × 0,22-0) = 0

S = E(a₃-a₂)/(C₂a₃ -С₄b₃) [13]

S = 0,27× (0,22 – ( - 0,09)/ (0,4 × 0,22 - (0 × (- 0,047)) = 0,269

В том случае, если судно по составу ДРК подпадает под вариант 6, то в выше приведенных выражениях величины Е и Е æ_r определяются следующим образом:

E = E₍₁₎ + E₍₂₎;

E æ_r = E æ_{r (1)} + E æ_{r (2)}

где индекс (1) относится к первому простому варианту;

индекс (2) относится ко второму варианту.

Систематические расчеты показывают, что: b₂ > 0, а₃ > 0, S > 0, Q > 0. Знак величины Р может различным.

Расчет характеристик установившейся циркуляции может быть произведен по следующей цепочке формул:

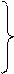β = - P – Q α_г + √( P + Q α_г )² + S α_г

Ω = [(C₁+ χ C₅) β +C₂ β²] / (m'- С₃ + χ С₆ - С₄ β) [14]

Θ = 1 / ( ³√1 + 2,7 Ω² )²

здесь α_г – угол перекладки рулевого выраженный в радианах.

Результаты расчета представляются в виде таблицы 2.2.

Таблица 2.2 – Диаграмма управляемости судна проекта № 785

αг	град
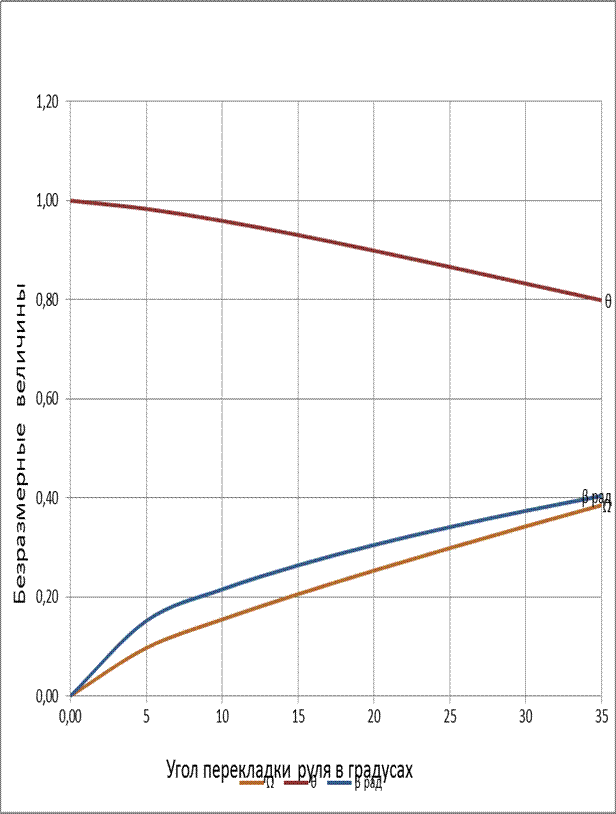
αг	рад.		0,09	0,17	0,26	0,35	0,44	0,52	0,61
β	рад		0,15	0,22	0,26	0,30	0,34	0,37	0,40
Ω	-		0,10	0,15	0,21	0,25	0,30	0,34	0,39
Θ	-		0,98	0,96	0,93	0,90	0,87	0,83	0,80
β	град	0,0000	8,69	12,32	15,11	17,46	19,54	21,41	23,13
R=L/ Ω	м		826,41	518,16	389,46	316,17	268,03	233,66	207,74
υц = υ0 Θ	м/с	5,6	5,51	5,37	5,21	5,04	4,85	4,66	4,47
T=2πR/υц	с		942,33	605,75	469,33	394,33	347,03	314,76	291,60

По данным таблицы 2.2 строится диаграмма управляемости .Рисунок 1.

Рисунок 1, Диаграмма управляемости судна

2.1.4 Расчет и построение траектории движения судна с отклоненным рулем.

Положение судна в любой момент времени t определяется двумя обобщенными координатами X₀ и Y₀ и углом курса ψ. Эти величины определяются по зависимостям :

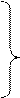X₀ = ∫ υ_xo dt

Y₀ = ∫ υ _yodt [15]

ψ = ∫ ωdt

После перехода к безразмерному времени "τ" и универсальным характеристикам β, Ω и с учетом выражений (15),(41) [1],

будем иметь:

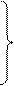X₀ = L ∫ Θ cos φ_s dτ

Y₀ = L ∫ Θ sin φ_s dτ [16]

ψ = φ_s + β

здесь φ_s - текущий угол скорости;

L - длина корпуса судна (м);

τ = υt / L - безразмерное время;

t - размерное время (с).

Эмпирические выражения для определения кинематических характеристик эволюционного движения имеют вид:

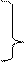β = β_ц χ(τ)

Θ = 1 - (1 - Θ_ц) ψ(τ) [17]

где β, Θ - соответственно угол дрейфа и падение скорости в данный момент времени эволюционного периода движения судна;

β_ц, Θ_ц – соответственно угол дрейфа и падение скорости на установившейся циркуляции при заданном угле перекладки руля.

Функции χ(τ) и ψ(τ) апроксимируются по выражениям :

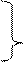χ(τ) =th^1.75(0.76 τ)

ψ(τ) = th^3.25 (0.43 τ) [18]

где th ( ) - гиперболический тангенс величины.

С удовлетворительной точностью значения функций χ(τ) и ψ(τ) можно определить по рис. 66 [1], задаваясь рядом значений величины безразмерного времени τ.

Величина угла скорости - φ_s определяется по рисунку 67 [1], по нижеприведенному выражению, вытекающему из (372) [1], в зависимости от Ω_ц и τ.

Ω_ц – определяется по таблице 2.2 при заданном угле перекладки.

φ_s = φ_s1 - φ_s2 - φ_s3

где φ_s1= Ω_ц τ (1+2,7 Ω_ц²)^-2/3;

φ_s2 =[10 Ω_ц (1 + 2.7 Ω_ц²)^-2/3 - Ω_ц (8.50 - 5.72 th^1.15(1,14 Ω_ц))](1- е^-0,8τ);

φ_s3 = 0.0446 (13 Ω_ц ^1.59 - sin 6 Ω_ц) τ е ^{–0,18τ – 0,167 τ2}

Как частный случай расчет траектории выполняется при максимальном угле перекладки рулевого органа. При ручном счете расчет траектории движения судна с отклоненным рулем рекомендуется выполнять в форме таблицы 2.3

α_r = 35 град. Ω_Ц = 1,1; β_ц = 0,473 рад.; Θ_ц = 0,387

Таблица 2.3 – Расчет траектории движения судна проекта № 507 при угле перекладки руля 35 градусов

Таблицу следует заполнять построчно. Интегральные суммы ∑₁ и ∑₂ определяются по следующей схеме: пусть а₁, а₂, а₃, …….a_n - величины в строке Θ cos φ_s, а величины для строки ∑ - b₁, b₂, b₃. . . .,b_n, тогда

b₁= a₁; b₂ = b₁ + a₁ + а₂; b₃ = b₂ + а₂ + а₃ и т.д.

Коэффициент - k равен половине шага интегрирования по τ , в данном случае составляет 0.5.

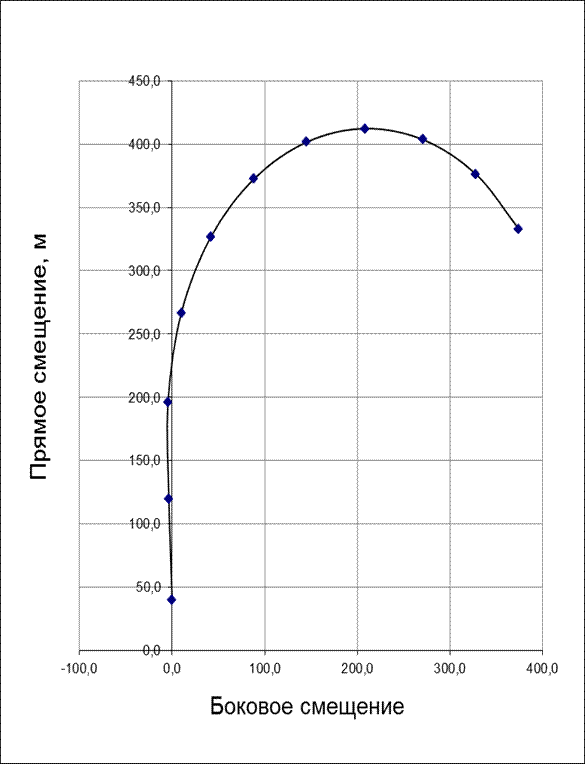
Траектория движения строится в одном масштабе по осям. Рисунок 3.
Систематические расчеты показывают, что если интегрирование ведется при τ, лежащем в пределах от 0 до 5, то чаще всего в результате будем иметь эволюционный период циркуляции и только самый начальный участок установившегося периода. Для получения полного вида циркуляции, необходимо: либо продолжить расчеты до τ , равного 8-10, либо применить графический способ построения и с помощью циркуля достроить период установившегося движения.

После построения траектории движения ЦТ судна и нескольких расчетных точках, используя угол курса, наносится положение диаметральной плоскости (в том же масштабе) и строятся траектории форштевня и ахтерштевня.

После завершения расчетов делаем общий вывод об управляемости судна с определением конкретных параметров характерных точек и величин циркуляции.

τ (задаем)	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0	10,0
χ(τ)	0,0	0,46	0,85	0,96	0,99	1,00	1,00	1,00	1,00	1,00	1,00
Ψ (τ)	0,0	0,05	0,31	0,61	0,81	0,92	0,96	0,98	0,99	1,00	1,00
β (рад)	0,0	0,19	0,34	0,39	0,40	0,40	0,40	0,40	0,40	0,40	0,40
Θ	1,0	0,99	0,94	0,88	0,84	0,82	0,81	0,80	0,80	0,80	0,80
φs (рад)	0,0	0,10	0,41	0,73	1,04	1,35	1,65	1,96	2,27	2,57	2,88
ψ (рад)	0,0	0,10	0,41	0,73	1,04	1,35	1,65	1,96	2,27	2,57	2,88
ψ (градус)	0,0	5,52	23,54	41,85	59,78	77,34	94,80	112,30	129,86	147,46	165,08
Cos φs	1,0	1,00	1,00	0,94	0,80	0,58	0,31	0,01	-0,29	-0,56	-0,79
Θ cos φs	1,0	0,99	0,94	0,83	0,67	0,48	0,25	0,01	-0,23	-0,45	-0,63
∑1Θcosφs	1,0	2,99	4,91	6,67	8,17	9,31	10,04	10,31	10,09	9,41	8,33
X0=kL∑1	40,0	119,42	196,26	266,76	326,61	372,47	401,69	412,30	403,56	376,32	333,12
Sin φs	0,0	-0,09	0,07	0,33	0,60	0,81	0,95	1,00	0,96	0,83	0,62
Θ sin φs	0,0	-0,09	0,07	0,29	0,50	0,66	0,77	0,80	0,77	0,66	0,49
∑2Θ sinφs	0,0	-0,09	-0,11	0,25	1,04	2,21	3,63	5,20	6,77	8,20	9,35
Y0=kL∑2	0,0	-3,52	-4,44	9,90	41,70	88,25	145,35	208,04	270,78	327,84	373,96

Вывод: Под управляемостью судна (состава) понимается совокупность двух важнейших навигационных характеристик – устойчивости на курсе и

поворотливости. Из расчетов и графика диаграммы направленности можно сделать заключение, что судно теоретически устойчиво на прямом курсе.

Поворотливость судна в первую очередь характеризуется диаметром или радиусом установившейся циркуляции. По графику траектории движения центра тяжести судна при перекладке руля на максимальный угол равный 35⁰ легко определить большинство геометрических характеристик. Судоводитель должен знать эти характеристики (тактический диаметр циркуляции, выбег и т.д.) при выполнении судном различных маневров – оборот перед занятым участком судового хода, подход к причалу при движении вниз, уклонение при расхождении со встречным судном и т.д.

Рис.2 – Траектория движения судна при угле перекладки руля 35 градусов