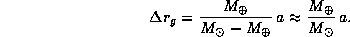Кинематика Солнечной системы. 4.1 Пытаясь определить расстояния планет от Солнца и их периоды обращения из

4.1 Пытаясь определить расстояния планет от Солнца и их периоды обращения из наблюдений, вы фактически оказываетесь в положении Иоганна Кеплера, в распоряжении которого как раз и были только "сырые" данные о положении планет на небесной сфере, и который определял по этим данным расстояния и периоды с тем, чтобы установить законы движения планет.

Итак, рассмотрим сначала нижнюю планету -- Венеру. Следует дождаться элонгации Венеры и измерить наибольший угол, на который планета удаляется от Солнца. Вы получите 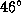. Нарисуйте нехитрый рисунок, изображающий круговые орбиты Земли и Венеры, произвольное положение Земли и Венеру в элонгации. Прямая Земля -- Венера при этом является касательной к орбите Венеры. Из рисунка очевидно, что синус угла элонгации, т.е. 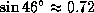, равен искомому радиусу орбиты Венеры в астрономических единицах.

Расстояние найдено, определим теперь из наблюдений период обращения ("забыв" про третий закон Кеплера). Следует дождаться повторения одной из конфигураций Венеры --например, восточной элонгации. Это даст синодический период обращения Венеры, 590 суток. Пользуясь уравнением синодического движения, найдем искомый сидерический период P:

откуда P= 225 суток.

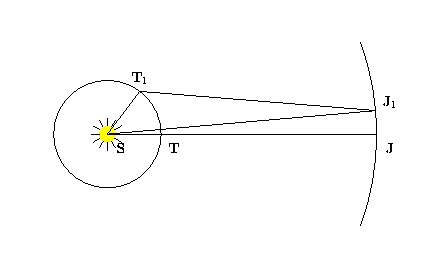
Перейдем к внешней планете -- Юпитеру. Наблюдения показывают, что после противостояния S-T-J (см. рис.) Юпитер движется 2 месяца попятным движением. Затем в течение 9 месяцев происходит прямое движение. После этого вновь начинается попятное движение, и через 2 месяца наступает следующее противостояние. Итак, синодический период обращения планеты, т.е. промежуток времени от одного противостояния до другого, равен T = 2+9+2 = 13 месяцам. Искомый сидерический период P найдем из уравнения синодического движения для внешней планеты:

где время измеряется в годах, откуда

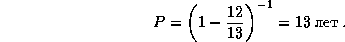
(Более аккуратные наблюдения дадут более точное значение, 12 лет.)

Вновь подавив в себе соблазн применить третий закон Кеплера, определим теперь из наблюдений расстояние от Юпитера до Солнца. Сделать это несколько труднее, чем в случае Венеры. Рассмотрим вновь момент противостояния, S-T-J. Через 2 месяца после этого (точнее, через 59 суток) наступит стояние Юпитера 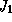; Земля при этом займет положение 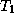. Угол 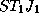можно измерить: 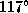. Угол же 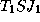можно вычислить: за 59 суток Земля проходит угол 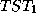в 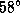, а Юпитер -- угол 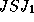, равный 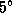, откуда 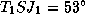. Теперь вычисляем угол 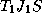: 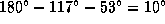. По теореме синусов имеем 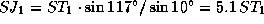. Радиус орбиты Юпитера найден: 5.1 а.е. (на самом деле -- 5.203 а.е.).

4.2 Перигелийное расстояние 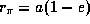для Плутона составляет 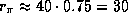а.е. Более точное значение: 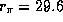а.е., так что в перигелии Плутон чуть ближе к Солнцу, чем Нептун, почти точно круговая (e = 0.0086) орбита которого имеет a = 30.1. Тесных сближений Нептуна и Плутона никогда не происходит. Периоды их обращения находятся в резонансе 3:2 (с какой точностью?). В начале XXII в. Плутон окажется вблизи афелия, и его расстояние от Солнца будет близко к 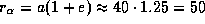а.е. Поэтому, если считать, что мгновенный размер Солнечной системы определяется расстоянием от Солнца до наиболее удаленной от него в данный момент планеты, то можно сказать, что он периодически изменяется от 30 до 50 а.е. См., впрочем задачу .

Период обращения Плутона вокруг Солнца 250 лет. Открыт он был Клайдом Томбо в 1930 г., т.е. 67 лет тому назад. За это время он сместился по орбите на угол . На самом деле смещение несколько больше (почему?).

4.3 По третьему закону Кеплера большая полуось орбиты Нептуна равна 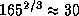а.е., т.е. Нептун находится в 30 раз дальше от Солнца, чем Земля. Угловой диаметр Солнца, видимый с Земли, равен примерно 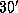. Следовательно, при наблюдении с Нептуна диск Солнца будет виден под углом 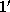, т.е. на пределе разрешения глаза. Реально увидеть диск будет нельзя -- Солнце "слепит глаза", и предельное разрешение достигаться не будет.

4.4 Вот соответствующий рисунок:

4.5 Поскольку большая полуось орбиты Юпитера равна 5 а.е., то вопрос, поставленный в задаче, можно переформулировать так: под каким углом видна 1 а.е., расположенная перпендикулярно к лучу зрения, с расстояния в 5 а.е.? Ответ очевиден: этот угол равен примерно 1/5 радиана, т.е. около .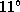

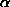4.6 Расстояние до Cen равно приблизительно 1.3 пк. По определению парсека, это означает, что большая полуось орбиты Земли, т.е. 1 а.е., расположенная перпендикулярно к лучу зрения, видна с 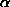Cen под углом 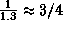угл. сек. Так как большая полуось орбиты Юпитера равна 5 а.е., а сама его орбита близка к круговой, то наибольшее угловое расстояние от Солнца, на котором Юпитер бывает виден с 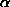Cen, составляет 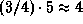угловых секунды.

4.7 Синодический период вращения Солнца для наблюдателя на Меркурии вычисляем по формуле синодического движения: 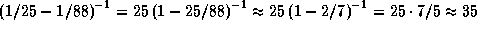суток (меркурианский год равен 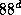). Плутон же движется чрезвычайно медленно, так что синодический период вращения Солнца практически совпадает с сидерическим, 25 суток. Синодический период при наблюдении с Земли вычислите самостоятельно.

4.8 Угловой диаметр диска Солнца составляет 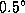. Расстояние от Солнца до Венеры 0.7 а.е., расстояние от Земли до Венеры в нижнем соединении 0.3 а.е. Поэтому, пересекая по диаметру диск Солнца, Венера проходит в своем синодическом движении дугу 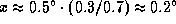(см. рис.). Для этого требуется 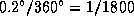ее синодического периода. Последний равен 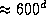(см. задачу ). Отсюда находим искомое время: около 8 часов.

В отличие от задачи про солнечное затмение, для ответа на вопрос о направлении перемещения Венеры по диску Солнца будем гелиоцентристами. Если смотреть на Солнечную систему со стороны северного полюса Земли, то и Венера, и Земля движутся вокруг Солнца против часовой стрелки, причем Венера быстрее, чем Земля. Поэтому вблизи нижнего соединения Венера перемещается по небу слева направо. Таким же будет и ее движение по диску Солнца.

4.9 Покрываемая звезда находится на много порядков дальше от Земли, чем Плутон. Поэтому конус тени, отбрасываемой Плутоном на Землю при покрытии, можно считать цилиндром, диаметр сечения которого равен диаметру Плутона, 2300 км. Это и есть оценка ширины полосы на поверхности Земли, в пределах которой можно наблюдать покрытие. [На самом деле надо учесть, что Земля не плоская, а шарообразная. Вследствие этого ширина полосы может достигать 5600 км; покажите это самостоятельно.]

Продолжительность покрытия определяется диаметром тени и скоростью ее движения по поверхности Земли. Орбитальная скорость Земли равна 30 км/с, Плутона -- в 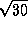раз меньше, так как скорость обратно пропорциональна корню из радиуса орбиты. [Оценивая скорость Плутона, мы пренебрегли эллиптичностью его орбиты. Нетрудно учесть ее и найти, что скорость Плутона в перигелии эллиптической орбиты с a = 40 а.е. и e = 0.25 примерно в 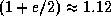раз выше скорости движения по круговой орбите радиуса 30 а.е.] Если во время покрытия вектор скорости Земли перпендикулярен оси цилиндра тени, то тень движется по поверхности Земли со скоростью Земли относительно Плутона, 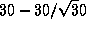км/с; если параллелен, то со скоростью Плутона, 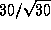км/с. Отсюда -- оценка продолжительности покрытия в том месте, где наблюдатель пересекает тень по диаметру: 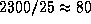c 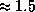мин в первом случае и 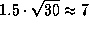мин во втором. В других местах продолжительность покрытия будет меньше.

Продолжительность покрытия 1988 г., которое наблюдалось восемью экспедициями в Австралии и Новой Зеландии и в ходе которого у Плутона была открыта атмосфера, составляла в среднем около минуты.

4.10 Мощность сигнала, приходящего на лоцируемое тело, пропорциональна . Мощность сигнала, приходящего от тела на Землю, также пропорциональна . Поэтому мощность эхо-сигнала пропорциональна 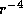. Здесь, как и в задаче , измеряемая величина убывает как четвертая степень расстояния, что в астрономических задачах встречается редко.

Расстояние от Земли до астероида в соединении 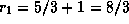а.е., в противостоянии 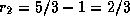а.е.; отношение расстояний 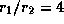. Значит, при локации астероида близ соединения следует послать сигнал, в 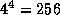раз более мощный, чем в противостоянии. Неожиданный, согласитесь, результат. Освещенность же от астероида в противостоянии лишь в 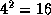раз больше, чем в соединении. Соответствующая разность звездных величин близка к .

Всемирное тяготение

5.1 Солнечная система разрушится. Планеты улетят от Солнца по параболам, поскольку скорость их движения по первоначальным (круговым) орбитам в точности равна параболической скорости при уменьшенной вдвое массе центрального тела. Возможно, Солнце сохранит Меркурий, Марс и Плутон. Однако если бы эта катастрофа случилась с Солнцем в течение нескольких ближайших лет (чего определенно не произойдет), то Плутон тоже наверняка был бы потерян -- он сейчас находится близ перигелия своей заметно некруговой орбиты. А про Марс и про Меркурий заранее сказать что-то трудно. Все будет зависеть от их положения на орбитах в тот момент, когда Солнце "похудеет". Если они окажутся близ афелиев, то сохранятся около Солнца, если же будут близ перигелиев, то улетят от него навсегда.

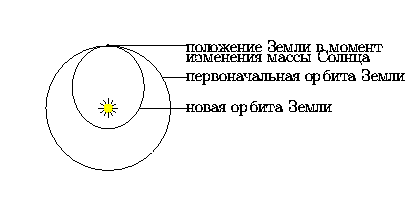
5.2 В момент внезапного увеличения массы Солнца Земля начинает испытывать вдвое большую, чем прежде, силу притяжения со стороны Солнца. Следовательно, она перейдет с круговой орбиты на эллиптическую, целиком лежащую внутри прежней орбиты (см. рис. на следующей странице). Таким образом, в момент схода с круговой орбиты Земля будет находиться в афелии своей новой эллиптической орбиты.

Интегралы энергии, описывающие движение Земли в поле центрального тела с массами, равными M и 2M, имеют соответственно следующий вид:

где a -- первоначальное и 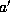-- новое значение большой полуоси орбиты Земли (после того как масса Солнца внезапно увеличилась вдвое). Сравнивая эти два выражения между собой, находим, что .

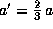Найдем период обращения Земли по новой орбите. По третьему закону Кеплера имеем

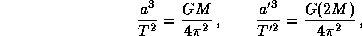
откуда

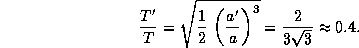
Эксцентриситет новой орбиты найдем из соотношения a = a'(1+e'), откуда e'=0.5.

5.3 Из приравнивания центробежной силы к силе тяготения следует, что (значение постоянной подсчитайте сами). Средние же плотности всех тел Солнечной системы отличаются меньше, чем на порядок. Они заключены между 0.7 г/см³ (Сатурн; соответствующее время облета -- 4.2 часа) и 5.5 г/см³ (Земля; облетев Землю за полтора часа, Гагарин установил тем самым первый в истории и по сей день единственный межпланетный рекорд).

Время облета Солнца, а потому одновременно и верхняя оценка возможного минимального периода осевого вращения звезд типа Солнца, в 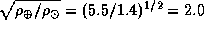раза больше минимального времени облета Земли и составляет, таким образом, всего около 3 часов! Не правда ли, удивительно? За это время проходится путь 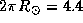млн км, скорость полета близка к 400 км/с -- в 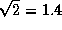раза меньше скорости убегания с "поверхности" Солнца.

У типичного белого карлика 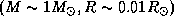средняя плотность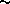 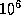г/см³, и потому время облета порядка 10 секунд, скорость же движения при этом всего 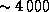км/с ("всего" -- это значит, что хотя по повседневным меркам она и велика, но все же .

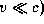Облет нейтронной звезды 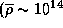г/см³) занял бы всего несколько миллисекунд и (при радиусе звезды 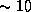км) происходил бы со скоростью во многие десятки тысяч км/с. Ясно, что, изучая нейтронные звезды, мы находимся у самой границы применимости классической механики. Релятивистские поправки для нейтронных звезд должны быть уже очень заметными.

Примечание (для "эрудитов"). То, что , следует и из обобщенного третьего закона Кеплера 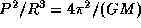. Однако не-эрудиты знают лишь, что 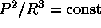, помнить же выражение для постоянной -- это и есть "эрудиция".

5.4 Из интеграла энергии

и выражений для расстояний в перигелии и в афелии

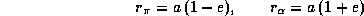
следует, что отношение соответствующих скоростей есть

Если оно равно 3, то e=0.5.

5.5 Пусть P -- период обращения в годах, r -- радиус орбиты в а.е. и v -- скорость движения по орбите в км/с. Поскольку орбитальная скорость Земли равна 30 км/с, то мы имеем, очевидно,

С другой стороны, по третьему закону Кеплера 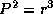, и поэтому

так что, например, Юпитер (r=5) движется по орбите со скоростью 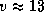км/с.

5.6 Запишем интеграл энергии для кометы, находящейся на гелиоцентрическом расстоянии Земли:

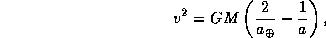
где 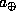-- большая полуось орбиты Земли, 1 а.е. Круговая скорость на орбите Земли есть

Так как по условию 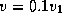, большая полуось оказывается равной

Период обращения находится отсюда по третьему закону Кеплера:

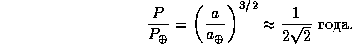
Он тот же, что и при падении на притягивающий центр по прямой, см. задачу . Из условия задачи следует, что комета на расстоянии 1 а.е. находится в афелии своей орбиты, так что афелийное расстояние есть 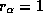а.е. Но 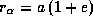, отсюда эксцентриситет

Следовательно, перигелийное расстояние будет чрезвычайно малым:

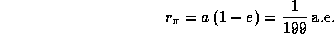
Это, кстати, около 750000 км, а значит, комета в перигелии почти "зацепит" Солнце. Такие кометы, "царапающие Солнце", неоднократно наблюдались.

5.7 Расстояния в перигее и в апогее

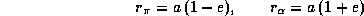
дают большую полуось орбиты спутника

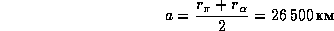
и ее эксцентриситет

Период обращения по третьему закону Кеплера равен

В эту формулу можно подставить числа, но вычисления можно существенно сократить следующим образом. Мы знаем, что низколетящий спутник совершает виток вокруг Земли за 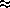1.5 часа ("гагаринское время"). Это значит, что при полуоси период 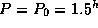. Записав третий закон Кеплера в относительной форме

получаем

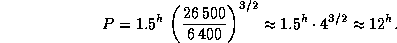
Действительно, "Молния" -- полусуточный спутник.

5.8 Большая полуось орбиты Земли -- 1 а.е., Марса -- 1.5 а.е. Период обращения Земли равен 1 году. Большая полуось гомановского эллипса равна, очевидно, полусумме радиусов орбит Земли и Марса: a=1.25 а.е. По третьему закону Кеплера период обращения для гомановской орбиты в годах равен

Искомое время перелета составляет половину периода обращения, т.е. около 8 месяцев.

5.9 Сидерический период вращения Солнца на экваторе 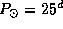, таков же период обращения космического аппарата на гелиостационарной орбите. Для Земли период обращения 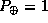год, большая полуось орбиты 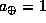а.е. По третьему закону Кеплера, выражая P и a в годах и в а.е., соответственно, имеем 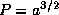, откуда находим радиус гелиостационарной орбиты:

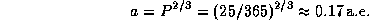
Без всяких вычислений можно было сразу утверждать, что гелиостационарная орбита лежит внутри орбиты Меркурия, период обращения которого вокруг Солнца равен 88 суткам, что существенно больше периода осевого вращения Солнца.

5.10 Как следует из закона сохранения энергии, какую бы скорость ни имело тело на границе сферы действия Луны, при касании лунной поверхности она не может быть меньше скорости убегания с поверхности Луны, 2.4 км/с.

5.11 Величины, относящиеся к Юпитеру, будем отмечать индексом J. Тогда отношение светимостей 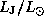равно доле поверхности сферы радиуса 5 а.е., которую занимает диск Юпитера:

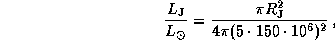
где 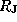-- радиус Юпитера в км. Учитывая, что радиус Юпитера 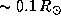, мы получаем

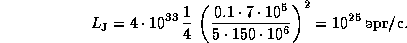
Искомый темп аккреции оценим по очевидной формуле (ср. решение задачи )

где 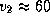км/с -- вторая космическая скорость для Юпитера.

Таким образом, если бы такая аккреция имела место, за время жизни Солнечной системы лет) масса Юпитера заметно не изменилась бы. Здесь уместно напомнить, что действительная светимость Юпитера примерно вдвое выше той, которая обеспечивается приходящим от Солнца излучением. Однако источник этой энергии следует искать в самом Юпитере, а не в аккреции.

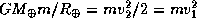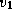5.12 Энергия, необходимая для доставки пылесоса на Луну, примерно равна , где и 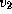-- первая и вторая космические скорости, m -- масса пылесоса. Энергия, выделяющаяся при работе пылесоса, равна PT, где P -- мощность его мотора, T -- время работы. Если принять P = 500 Вт 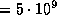эрг/с, m = 5 кг, то получим: 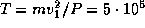с 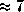суток. Всего нужно, таким образом, около 80 кВт час, а это стоит (в ценах конца 1996 г.) всего каких-то руб. См. также задачу .

5.13 Ответ таков: предельный радиус составляет около 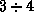км, если прыгать вверх, не разбегаясь, и несколько больше, если сначала разбежаться. Вот соответствующий расчет.

Ясно, что в момент отрыва от поверхности астероида прыгун должен развить вторую космическую скорость

Второе выражение для v, безусловно, больше подходит для наших целей, так как среднюю плотность астероида оценить не составляет труда: заключено между 1 г/см³ (лед) и 8 г/см³ (железо). Мы в дальнейшем будем брать г/см³. Итак,

Вертикальную составляющую скорости прыгуна при прыжке на Земле можно оценить по формуле

где g -- земное ускорение силы тяжести и h -- высота, на которую центр тяжести поднимается в прыжке. В качестве разумной оценки возьмем h=1 м (тогда прыгун преодолеет планку на высоте 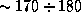см -- космонавт, оказавшийся на астероиде, надо думать, хорошо тренирован).

В итоге радиус астероида, с которого можно, подскочив вверх, улететь в открытый космос, оказывается равен

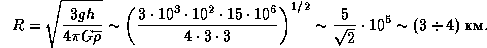
Если, однако, перед прыжком космонавт разбежится, то он сумеет спрыгнуть и с тела большего размера. На астероиде разбег дает неожиданный эффект, с которым земные спортсмены не знакомы. На астероиде размером в несколько километров, имея хорошие шиповки, легко разбежаться до первой космической скорости (проверьте!). А тогда за счет прыжка вверх нужно будет преодолевать меньший потенциальный барьер.

5.14 У спутника, движущегося по круговой орбите, центробежная сила уравновешивает силу притяжения, что дает

Обозначим через и 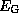, соответственно, кинетическую и потенциальную энергию в расчете на единицу массы спутника. Тогда последнее равенство можно записать также так:

Пусть, далее, E -- полная энергия спутника:

Эти соотношения дают

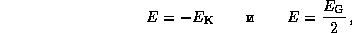
откуда 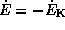. Это равенство означает, что, действительно, темп потерь энергии на трение о воздух 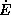(отрицательная величина -- энергия расходуется) равен темпу прироста кинетической энергии спутника 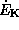(положительному!). Откуда же эта энергия черпается? Очевидно, что из потенциальной энергии -- другого источника нет. Действительно, так как 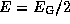(см. выше), то 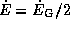, так что спутник получает лишь половину выделяющейся гравитационной энергии, вторая же половина переходит в тепло.

Таким образом, в ньютоновском поле тяготения действует своеобразная "мораль", близкая к христианской: отдавая энергию в окружающую среду, -- так сказать, делая ей "добро", -- движущееся тело само от этого становится "добрее", т.е. приобретает кинетическую энергию. Вся эта энергия, как отдаваемая, так и в результате этого приобретаемая, черпается из потенциальной энергии, выступающей, если угодно, в роли "веры," рождающей "добро".

Хотя приведенное выше доказательство совершенно верно, оно тем не менее может оставить у читателя какое-то чувство неудовлетворенности. Попробуем пояснить удивительный результат, который мы обсуждаем, -- его иногда называют вириальным парадоксом -- совсем "на пальцах". Луна движется по своей орбите со скоростью км/с. Если бы она двигалась в сопротивляющейся среде, то стала бы медленно "падать вниз" -- это кажется очевидным. Со временем она превратилась бы в низколетящий спутник, а скорость его движения, как все знают, близка к 8 км/с. Таким образом, кинетическая энергия многократно возросла бы -- и это почему-то никого не удивляет! По сути же дела это в точности то же самое, что мы обсуждали выше.

5.15 Поскольку в условии задачи употреблено сослагательное наклонение, это означает, что на самом деле путь Луны относительно Солнца, т.е. ее орбита в Солнечной системе, точек перегиба не имеет и везде обращена выпуклостью от Солнца. Этот факт мало кто знает, и он кажется неожиданным.

Понятно, что кривизна траектории Луны в Солнечной системе меняется с синодическим периодом, являясь наибольшей в полнолунии и наименьшей в новолунии. Чтобы выпуклость даже в новолунии была обращена от Солнца, надо, чтобы равнодействующая сил притяжения Луны к Солнцу и к Земле была бы направлена к Солнцу. Иначе говоря, сила притяжения Луны к Солнцу 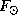должна быть больше, чем сила ее притяжения к Земле 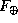. Мы имеем:

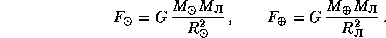
Отсюда

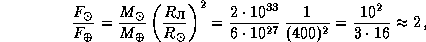
так что Луна притягивается к Солнцу примерно вдвое сильнее, чем к Земле. Не правда ли, любопытный факт?

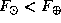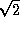Чтобы на лунной орбите в Солнечной системе были бы точки перегиба, в новолунии должно быть , так что расстояние до Луны должно было бы быть тыс. км (множитель здесь не точный, он взят из полученной выше оценки значения 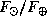в "реальной" Солнечной системе).

См. также задачу .

5.16 В курсе общей астрономии обсуждают океанские приливы, вызываемые притяжением Луны (и Солнца). Однако если сила тяжести существенно меняется на расстояниях м, вполне ощутимые приливы будут возникать и в теле человека. Действительно, приливное ускорение равно

где M -- масса звезды, l -- характерный размер тела космонавта, r -- расстояние от космического аппарата до центра звезды. Если вы не помните этого выражения, получите его самостоятельно, записав ускорения, сообщаемые звездой наиболее и наименее удаленной от нее точкам тела и вычислив разность этих ускорений в пренебрежении малыми величинами, начиная с квадрата l/r. Предельной будем считать перегрузку a = 2 g, где g -- ускорение силы тяжести на поверхности Земли. Тогда

откуда

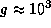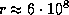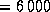Типичная масса нейтронной звезды ; характерный размер тела человека l = 100; (система СГС). Отсюда см км.

Поскольку радиус Солнца на два порядка больше этой величины, ясно, что при подлете к Солнцу космонавту угрожали бы совсем не приливные силы. Опасными факторами будут высокая температура, жесткое излучение и т.п.

5.17 На первый взгляд, должно выполняться следующее условие: сила притяжения спутника к астероиду должна превосходить силу притяжения его к Солнцу. Условие равенства двух сил записывается в виде

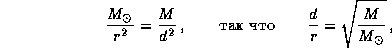
где M -- масса астероида, r -- гелиоцентрическое расстояние астероида, d -- искомое расстояние между астероидом и его спутником. Масса 100-километрового астероида (при плотности 2 г/см³) составляет 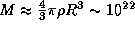г. Поэтому 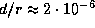. Полагая r = 3 а.е. 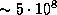км, находи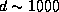м км.

Однако если те же рассуждения применить не к спутнику астероида, а к спутнику Земли, максимальное расстояние окажется равным 260000 км (см. задачу ). Луна находится на значительно большем расстоянии! Парадокс легко разрешается: на самом деле надо рассматривать не ускорение, сообщаемое спутнику Солнцем, а разность ускорений, сообщаемых спутнику и телу, вокруг которого он движется. Эта разность, как легко показать, не превосходит величины 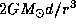(ср. решение предыдущей задачи), и потому уравнение для определения d имеет вид

откуда

С теми же числовыми значениями получаем для нашего двойного астероида 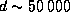км.

Вам, может быть, интересно будет знать, каков же на самом деле минимальный радиус круговой орбиты спутника, при котором он может покинуть астероид и начать двигаться по гелиоцентрической орбите. Его определение -- это непростая задача даже для профессионалов - небесных механиков. Соответствующий радиус 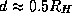, где

называется радиусом Хилла. Как видно, наша оценка совсем неплоха.

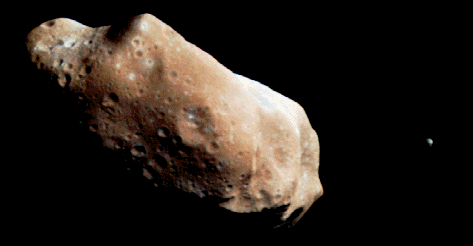Ида и ее спутник Дактил

А теперь -- от сухой теории к живой сегодняшней астрономии. Космический зонд "Галилей" на своем пути к Юпитеру испытал сближение с астероидом Ида и передал его изображение. Неожиданно обнаружилось, что у Иды есть миниатюрный спутник. Изображение Иды с ее спутником см. также в Интернете по адресу http://galileo.ivv.nasa.gov/idamoon.html

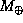5.18 Обозначим через и 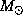массы Земли и Солнца, через a -- расстояние между ними. Введем систему координат, как показано на рисунке внизу.

Ясно, что искомая поверхность обладает осевой симметрией относительно оси абсцисс. Поэтому достаточно найти сечение поверхности плоскостью XY, т.е. уравнение плоской кривой вида f(x,y)=0.

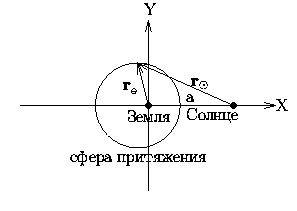
Записывая условие равенства сил притяжения к Солнцу и к Земле

и учитывая, что

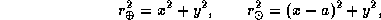
после несложных преобразований получаем уравнение сферы тяготения:

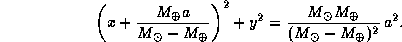
Таким образом, сфера тяготения -- это действительно сфера. Ее радиус равен

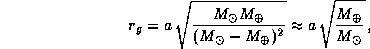
а центр смещен по оси x от центра Земли в противосолнечном направлении на расстояние