Равнопеременное криволинейное движение
Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: 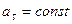 . Найдем закон этого движения, считая, что при
. Найдем закон этого движения, считая, что при 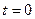 :
: 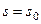 , а
, а 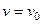 , где
, где 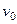 - начальная скорость точки. Согласно формуле
- начальная скорость точки. Согласно формуле 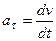 имеем
имеем 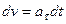 .
.
Так как 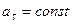 , то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:
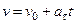 .
.
Формулу представим в виде
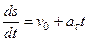 или
или 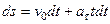 .
.
Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде
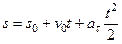 .
.
Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.
Свободное падение тел. Ускорение свободного падения
Свободное падение - это движение тела под действием только силы тяжести.
На тело, падающее в воздухе, кроме силы тяжести действует сила сопротивления воздуха, следовательно, такое движение не является свободным падением. Свободное падение — это падение тел в вакууме.
Ускорение  , которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.
, которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.
Ускорение свободного падения  направлено вертикально вниз.
направлено вертикально вниз.
Галилео Галилей установил (закон Галилея): все тела падают на поверхность Земли под действием земного притяжения при отсутствии сил сопротивления с одинаковым ускорением, т.е. ускорение свободного падения не зависит от массы тела.
Убедиться в этом можно, используя трубку Ньютона или стробоскопический метод.
Трубка Ньютона представляет собой стеклянную трубку длиной около 1 м, один конец которой запаян, а другой снабжен краном (рис. 25).
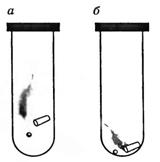
Рис.25
Поместим в трубку три разных предмета, например дробинку, пробку и птичье перо. Затем быстро перевернем трубку. Все три тела упадут на дно трубки, но в разное время: сначала дробинка, затем пробка и, наконец, перо. Но так падают тела в том случае, когда в трубке есть воздух (рис. 25, а). Стоит только воздух откачать насосом и снова перевернуть трубку, мы увидим, что все три тела упадут одновременно (рис. 25, б).
В земных условиях g зависит от географической широты местности.
Наибольшее значение оно имеет на полюсе g=9,81 м/с2, наименьшее — на экваторе g=9,75 м/с2. Причины этого:
1) суточное вращение Земли вокруг своей оси;
2) отклонение формы Земли от сферической;
3) неоднородное распределение плотности земных пород.
Ускорение свободного падения зависит от высоты h тела над поверхностью планеты. Его, если пренебречь вращением планеты, можно рассчитать по формуле:
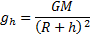
где G — гравитационная постоянная, М — масса планеты, R — радиус планеты.
Как следует из последней формулы, с увеличением высоты подъема тела над поверхностью планеты ускорение свободного падения уменьшается. Если пренебречь вращением планеты, то на поверхности планеты радиусом R
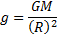
Для небольших высот (g<<h) можно считать g=const, для таких высот свободное падение является равноускоренным движением.
Для его описания можно использовать формулы равноускоренного движения:
уравнение скорости: 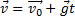
кинематическое уравнение, описывающее свободное падение тел: 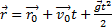 ,
,
или в проекции на ось 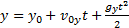 .
.
Движение тела, брошенного вертикально
Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости ( 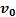 =0) (рис. 26).
=0) (рис. 26).
При выбранной системе координат движение тела описывается уравнениями: 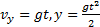 .
.
Из последней формулы можно найти время падения тела с высоты h:
 .
.
Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения: 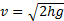 .
.
Движение тела, брошенного вертикально вверх с начальной скоростью 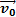 (рис. 27)
(рис. 27)
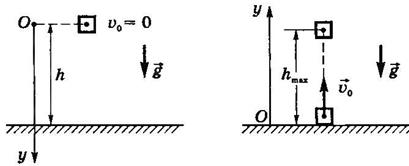
Рис.26 Рис.27
Движение тела описывается уравнениями: 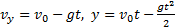
Из уравнения скорости видно, что тело движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при y=hmax скорость 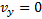 и в момент достижения телом первоначального положения у=0, можно найти:
и в момент достижения телом первоначального положения у=0, можно найти:
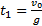 — время подъема тела на максимальную высоту;
— время подъема тела на максимальную высоту;
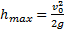 — максимальная высота подъема тела;
— максимальная высота подъема тела;
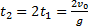 — время полета тела;
— время полета тела;
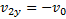 — проекция скорости в момент достижения телом первоначального положения.
— проекция скорости в момент достижения телом первоначального положения.
Движение тела, брошенного горизонтально
Если скорость 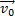 направлена не вертикально, то движение тела будет криволинейным.
направлена не вертикально, то движение тела будет криволинейным.
Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью 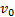 (рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что
(рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что 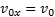 ,
, 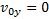 ,
, 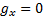 ,
, 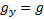 .
.
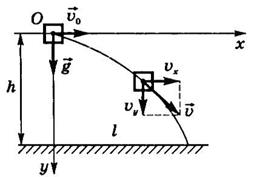
Рис.28
Тогда движение тела опишется уравнениями:
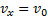 ,
, 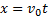 (3)
(3)
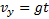 ,
, 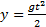 (4)
(4)
Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т.е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением g, т.е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (3) найдем время
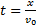 и, подставив его значение в формулу (4), получим:
и, подставив его значение в формулу (4), получим: 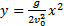
Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе (см. рис. 28). Модуль скорости можно рассчитать по теореме Пифагора:
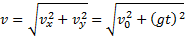
Зная высоту h, с которой брошено тело, можно найти время t1, через которое тело упадет на землю. В этот момент координата у равна высоте у1=h. Из уравнения (4) находим: 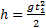
Отсюда
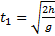 (5)
(5)
Формула (5) определяет время полета тела. За это время тело пройдет в горизонтальном направлении расстояние l, которое называют дальностью полета и которое можно найти на основании формулы (3), учитывая, что l=x1. Следовательно, 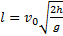 — дальность полета тела. Модуль скорости тела в этот момент
— дальность полета тела. Модуль скорости тела в этот момент 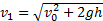 .
.
Движение тела, брошенного под углом к горизонту
Пусть тело брошено под углом α к горизонту со скоростью 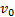 . Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ох и Оу (рис. 29).
. Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ох и Оу (рис. 29).
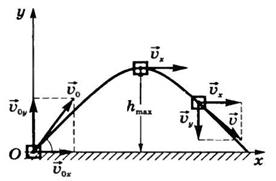
Рис.29
Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Оу и Ох: 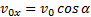 ,
, 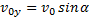 . Проекции ускорения:
. Проекции ускорения: 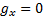 ,
, 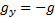
Тогда движение тела будет описываться уравнениями:
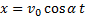 (6)
(6)
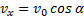 (7)
(7)
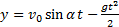 (8)
(8)
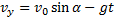 (9)
(9)
Из этих формул следует, что в горизонтальном направлении тело движется равномерно, а в вертикальном — равноускоренно.
Траекторией движения тела будет парабола. Учитывая, что в верхней точке параболы 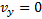 , можно найти время подъема тела до верхней точки параболы:
, можно найти время подъема тела до верхней точки параболы:
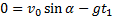

Подставив значение t1 в уравнение (8), найдем максимальную высоту подъема тела:
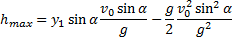
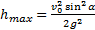 — максимальная высота подъема тела.
— максимальная высота подъема тела.
Время полета тела находим из условия, что при t=t2 координата у2=0. Следовательно, 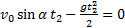 . Отсюда,
. Отсюда, 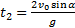 — время полета тела. Сравнивая эту формулу с формулой (10), видим, что t2=2t1.
— время полета тела. Сравнивая эту формулу с формулой (10), видим, что t2=2t1.
Время движения тела с максимальной высоты t3=t2-t1=2t1-t1=t1. Следовательно, сколько времени тело поднимается на максимальную высоту, столько времени оно опускается с этой высоты. Подставляя в уравнение координаты х (6) значение времени t2, найдем:
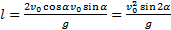 - дальность полета тела.
- дальность полета тела.
Мгновенная скорость в любой точке траектории направлена по касательной к траектории (см. рис. 29), модуль скорости определяется по формуле
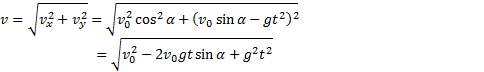
Таким образом, движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).
Методические рекомендации по решению задач
Несмотря на большое разнообразие задач по кинематике, можно предложить следующий алгоритм их решения:
1. Сделать схематический рисунок, изобразив начальное положение тел и их начальное состояние, т.е. 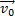 и
и 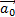 .
.
2. Выбрать систему отсчета на основании анализа условия задачи. Для этого нужно выбрать тело отсчета и связать с ним систему координат, указав начало отсчета координат, направление осей координат, момент начала отсчета времени. При выборе положительных направлений руководствуются направлением движения (скорости) или направлением ускорения.
3. Составить на основании законов движения систему уравнений в векторном виде для всех тел, а затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений следует обратить внимание на знаки "+" и "-" проекций входящих в них векторных величин.
4. Ответ необходимо получить в виде аналитической формулы (в общем виде), а в конце произвести числовые расчеты.
Пример 4. Сколько времени пассажир, сидящий у окна поезда, который идет со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, а длина 250 м?
Дано: 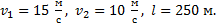
Найти: t.
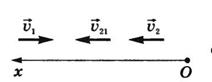
Решение. Неподвижную систему отсчета свяжем с Землей, подвижную – с поездом, в котором находится пассажир. Согласно закону сложения скоростей 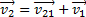 , где
, где 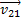 - скорость встречного поезда относительно первого. В проекциях на ось Ох:
- скорость встречного поезда относительно первого. В проекциях на ось Ох:
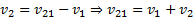 .
.
Так как путь, пройденный встречным поездом относительно первого, равен длине поезда, то время
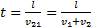 , t=10 c.
, t=10 c.
Пример 5. Пароход идет от Нижнего Новгорода до Астрахани 5,0 суток, а обратно - 7,0 суток. Как долго будет плыть плот от Нижнего Новгорода до Астрахани? Стоянки и задержки в движении исключить.
Дано: t1=5 сут, t2=7 сут.
Найти: t3
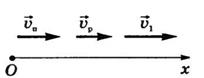
Решение. Неподвижную систему отсчета свяжем с берегом, подвижную – с водой. Будем считать, что скорость воды на всем пути одинакова и скорость парохода относительно воды постоянна и равна модулю мгновенной скорости парохода относительно воды.
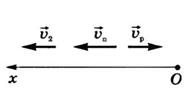
Так как плот движется относительно берега со скоростью течения реки 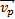 , то время его движения
, то время его движения 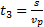 , где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей
, где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей 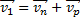 , или в проекциях на ось Ох:
, или в проекциях на ось Ох:
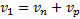 (1)
(1)
где 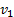 - скорость парохода относительно берега,
- скорость парохода относительно берега, 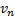 - скорость парохода относительно реки.
- скорость парохода относительно реки.
Зная время движения, можно найти скорость:
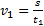 (2)
(2)
Из формул (1) и (2) имеем:
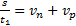 (3)
(3)
При движении парохода против течения 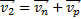 , или в проекциях на ось Ох
, или в проекциях на ось Ох 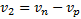 , где
, где 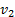 - скорость парохода относительно берега.
- скорость парохода относительно берега.
С другой стороны, 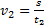 . Тогда
. Тогда
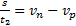 (4)
(4)
Решая систему уравнений (3) и (4) относительно 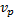 , получим:
, получим:
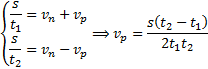
Найдем время движения плота:
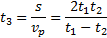
t3=35 сут.
Пример 6. При равноускоренном движении тело проходит за два первых равных последовательных промежутка времени по 4,0 с каждый пути s1 = 24 м и s2=64 м соответственно. Определите начальную скорость и ускорение тела.
Дано: t1=t2= 4,0 с, s1 =24 м, s2 = 64 м.
Найти: 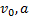 .
.
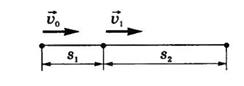
Решение. Запишем уравнения пути для s1 и (s1+s2) соответственно. Так как начальная скорость в этом случае одинакова, то
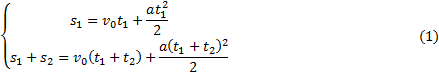
Так как t1=t2, то
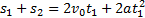 (2)
(2)
Выразив из (1) 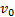 и подставив ее в (2), получим:
и подставив ее в (2), получим:
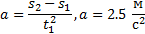
Тогда начальная скорость 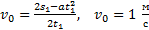
Пример 7. Автомобиль, двигаясь по прямолинейной траектории равноускоренно с начальной скоростью 5,0 м/с, прошел за первую секунду путь, равный 6,0 м. Найдите ускорение автомобиля, мгновенную скорость в конце второй секунды и перемещение за 2,0 с.
Дано: 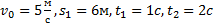
Найти: 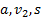
Решение. Зная путь, пройденный телом за первую секунду, можно найти ускорение:
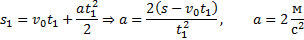
Скорость в конце второй секунды найдем по формуле
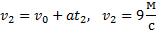
Перемещение за 2 с можно рассчитать по формулам:
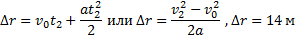
Пример 8.Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x = A + Bt + Ct3, где А=4 м, В=2м/с, С=-0,5 м/с3.
Для момента времени t1=2 c определить: 1) координату точки х1 точки; 2) мгновенную скорость v1; 3) мгновенное ускорение а1.
Дано: x = A + Bt + Ct3, А=4 м, В=2 м/с, С=-0,5 м/с3, t1=2 c.
Найти: х1; v1; а1.
Решение. 1.Подставим в уравнение движения вместо t заданное значение времени t1: x1 = A + Bt1 + Ct13. Подставим в это выражение значения А, В, С, t1 и произведем вычисления: х1 = 4 м.
2. Мгновенная скорость: 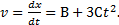 Тогда в момент времени t1 мгновенная скорость v1 = B + 3Ct12. Подставим сюда значения В,С, t1: v1= – 4 м/с. Знак минус указывает на то, что в момент времени t1=2 c точка движется в отрицательном направлении координатной оси.
Тогда в момент времени t1 мгновенная скорость v1 = B + 3Ct12. Подставим сюда значения В,С, t1: v1= – 4 м/с. Знак минус указывает на то, что в момент времени t1=2 c точка движется в отрицательном направлении координатной оси.
3. Мгновенное ускорение: 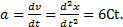 Мгновенное ускорение в момент времени t1 равно а1 = 6Сt1. Подставим значения С, t1: а1= –6 м/с2. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
Мгновенное ускорение в момент времени t1 равно а1 = 6Сt1. Подставим значения С, t1: а1= –6 м/с2. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
Пример 9.Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = A + Bt + Ct2, где А=5 м, В=4м/с, С= -1м/с2. Определить среднюю скорость vхср за интервал времени от t1=1 c до t2=6 c.
Дано: х = A + Bt + Ct2 , А=5м, В=4м/с, С=- 1м/с2, t1=1 c , t2=6 c.
Найти: vхср -? ахср -?
Решение. Средняя скорость за интервал времени t2-t1 определяется выражением vср=(х2-х1)/(t2- t1).
х1 = A + Bt1 + Ct12= 8 м, х2 = A + Bt2 + Ct22= –7 м.
Подставим значения х1, х2, t1 , t2 и произведем вычисления: vхср= -3 м/с.
Пример 10.Из вертолета, находящегося на высоте h = 300 м, сбросили груз. Через какое время груз достигнет земли, если: а) вертолет неподвижен; б) вертолет опускается со скоростью v0=5 м/с; 3) вертолет поднимается со скоростью v0=5 м/с. Описать графически соответствующие движения груза в осях s(t), v(t) и a(t).
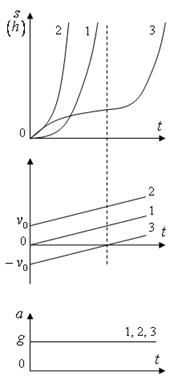
Решение.а) Груз, покинувший неподвижный вертолет, свободно падает, т.е. движется равноускоренно с ускорением свободного падения g. Время движения найдем из соотношения 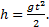 Откуда
Откуда 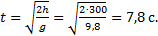 Графики движение объекта отмечены 1 на рисунке.
Графики движение объекта отмечены 1 на рисунке.
б) Движение груза, покинувшего вертолет, который опускается с постоянной скоростью v0=5 м/с, является равноускоренным движением с постоянным ускорением g и описывается уравнением 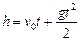 . Подстановка численных значений дает уравнение
. Подстановка численных значений дает уравнение 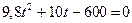 .
.
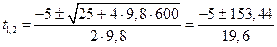 .
.
Отрицательный результат не имеет физического смысла, поэтому время движения t=7,57 с.
Графики движение объекта отмечены 2 на рисунке.
3) Движение груза, покинувшего вертолет, который поднимается с постоянной скоростью v0=5 м/с, cостоит из двух этапов. На первом этапе – груз движется равнозамедленно с постоянным ускорением g, направленным противоположно скорости, и описывается уравнениями 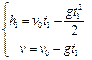 .
.
В верхней точке траектории скорость становится равной нулю, поэтому 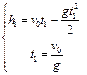 .
.
Подставляя второе уравнение системы в первое, получим 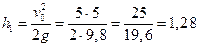 м.
м.
На втором этапе – свободное падение с высоты 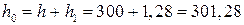 м.
м.
Поскольку 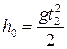 , то
, то 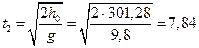 м.
м.
Графики движение объекта отмечены 3 на рисунке.
Пример 11.С воздушного шара, опускающегося вниз с постоянной скоростью 2 м/с, бросили вертикально вверх груз со скоростью 18 м/c относительно земли. Определить расстояние между шаром и грузом в момент, когда груз достигает высшей точки своего подъема. Через какое время груз пролетит мимо шара, падая вниз.
Дано: v01= 2 м/с, v02=18 м/c
Найти: s-? τ -?
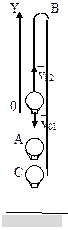
Решение. Направим ось 0Y вертикально вверх, начало совместим с точкой 0, в которой находился шар в момент бросания груза.
Тогда уравнения движения груза и воздушного шара:
у1= – v01t; y2 = v02t-gt2/2.
Скорость движения груза изменяется по закону v2=v02 – gt.
В наивысшей точке В подъема груза v2=0. Тогда время подъема до этой точки tпод=v02/g. Координата груза в точке В
y2В=v02tпод – gt2под /2= v022/2g.
За это время воздушный шар опустился до точки А; его координата
у1А= – v01tпод= – v01∙v02/g.
Расстояние между точками А и В: s=y2B – y1A= v022/2g+ v01∙v02/g.
Через промежуток времени τ, когда камень пролетит мимо шара, координаты тел будут одинаковы: у1С=у2С;
– v01τ = v02t – gt2/2.
Отсюда τ = 2(v01+v02)/g ≈ 4 c.
Пример 12.С какой скоростью и по какому курсу должен лететь самолет, чтобы за два часа пролететь на север 300 км, если во время полета дует северо-западный ветер под углом 30о к меридиану со скоростью 27 км/ч?
Дано: t=7,2∙103 c; l=3∙105 м; α=30° ≈ 0,52 рад; v2 ≈7,2 м/с.
Найти: v2 -? φ -?
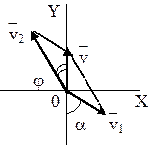
Решение. Рассмотрим движение самолета в системе отсчета, связанной с землей.
Проведем ось ОХ в направлении на восток, а ось OY - на север. Тогда скорость движения самолета в выбранной системе отсчета
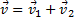 (1)
(1)
где v=l/t (2)
Уравнение (1) в проекции на оси
ОХ: 0=v1∙sinα – v2∙sinφ;
OY: v= v2∙cosφ - v1∙cosα, или v1∙sinα = v2∙sinφ, v2∙cosφ=v1∙cosα + v (3)
Разделив эти уравнения почленно, получим tgφ=v1sinα/(v1cosα+ v),
или с учетом (2)
tgφ=v1∙sinα/(v1∙cosα+ l/t);
φ=arctgv1∙sinα/(v1∙cosα+ l/t) ≈0,078 рад.
Возводя в квадрат правые и левые части уравнений (3) и складывая полученные уравнения, находим
v22∙sin2φ + v22 ∙cos2j = v12 sin2α+ (v1∙cosα + v)2,
откуда 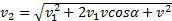 , или с учетом (2)
, или с учетом (2)
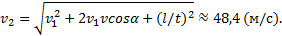
Пример 13.Тело, брошенное вертикально вверх, вернулось на землю через t=3 с. Найти высоту подъема тела и его начальную скорость.
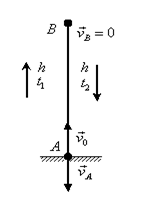
Решение.Движение тела вверх является равнозамедленным с ускорением - g и происходит в течение времени t1, а движение вниз – равноускоренным с ускорением g и происходит в течение времени t2. Уравнения, описывающие движение на участках АВ и ВА, образуют систему:
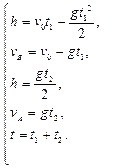
Поскольку 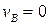 , то
, то 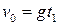 . Подставив v0 в первое уравнение системы, получим
. Подставив v0 в первое уравнение системы, получим 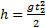 . Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t1=t2=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют
. Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t1=t2=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют 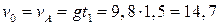 м/с.
м/с.
Высота подъема тела
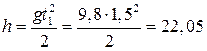 м.
м.
Пример 14.Свободно падающее тело в последнюю секунду движения прошло половину пути. Найти высоту, с которой оно брошено и время движения.
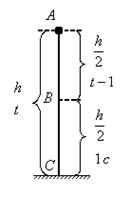
Решение.Зависимость пройденного пути от времени для свободно падающего тела 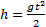 . Поскольку участок ВС, составляющие половину всего пути, пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как
. Поскольку участок ВС, составляющие половину всего пути, пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как 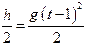 .
.
Решая систему 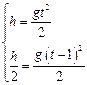 получим
получим 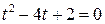 . Корни этого уравнения t1=3,41 с и t2=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно, тело падало в течение 3,41 с и прошло за это время путь
. Корни этого уравнения t1=3,41 с и t2=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно, тело падало в течение 3,41 с и прошло за это время путь 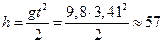 м.
м.
Пример 15.С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с.
Найти: 1) сколько времени камень будет в движении, 2) на каком расстояниион упадет на землю, 3) с какой скоростью он упадет на землю, 4) какой угол составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать.
Дано: Н=25 м, vo=15 м/с
Найти: t-? sx- ? v - ? φ- ?
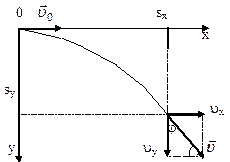
Решение. Перемещение брошенного горизонтально камня можно разложить на два: горизонтальное sx и вертикальное sy:
sy=H=gt2/2,
sx=vot,
где t - время движения.
Отсюда:
1) 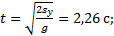
2) sx=vot= 33,9 м;
3) vy=gt=22,1м/с;
4) sinφ= vy/v=0,827;
φ=55о48’.
Пример 16.С башни высотой 25 м горизонтально со скоростью vx=10 м/c брошено тело.
Найти: 1) время t падения тела, 2) на каком расстоянии l от основания башни оно упадет, 3) скорость v в конце падения, 4) угол, который составит траектория тела с землей в точке его приземления.
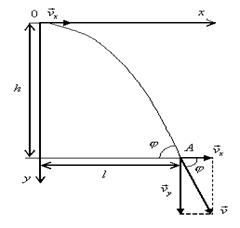
Решение.Движение тела является сложным. Оно участвует в равномерном движении по горизонтали и равноускоренном с ускорением g по вертикали. Поэтому участок АВ описывается уравнениями:
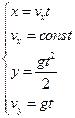
Для точки А эти уравнения принимают вид:
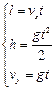
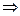
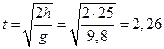 с
с
Тогда 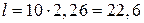 м, а
м, а 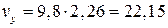 м/с.
м/с.
Поскольку 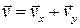 , то
, то 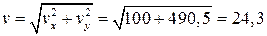 м/с.
м/с.
Угол, который траектория составляет с землей, равен углу φ в треугольнике скоростей в т. А, тангенс которого 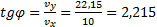 , поэтому φ=68,7°.
, поэтому φ=68,7°.
Пример 17.Для тела, брошенного с горизонтальной скоростью vx=10 м/с, через время t=2 с после начала движения найти: нормальное, тангенциальное и полное ускорения, а также радиус кривизны траектории в этой точке.
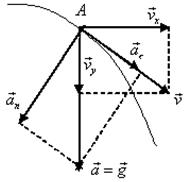
Решение.Вертикальная составляющая скорости 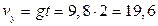 м/с
м/с
Скорость в точке А:
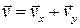 ,
, 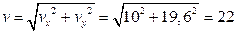 м/с .
м/с .
Векторы 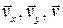 образуют треугольник скоростей, а векторы
образуют треугольник скоростей, а векторы 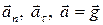 - треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны:
- треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны: 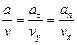 .
.
Отсюда, 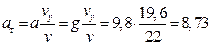 м/с2,
м/с2,
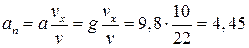 м/с2.
м/с2.
Нормальное ускорение 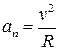 , поэтому радиус кривизны траектории
, поэтому радиус кривизны траектории
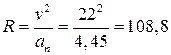 м.
м.
Пример 18.Мяч бросили со скоростью 10 м/с под углом 40о к горизонту.
Найти: 1) на какую высоту поднимется мяч; 2) на каком расстоянии от места бросания мяч упадет на землю, 3) сколько времени он будет в движении.
Дано: vo=10 м/с, α=40о.
Найти: sy - ? sx - ? t - ?
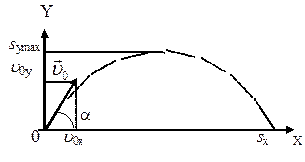
Решение. 1) Найдем наибольшую высоту sy max, на которую поднимается тело, брошенное со скоростью vo подуглом α к горизонту. Имеем (см. рис.):
vy=vo sinα – gt; (1)
sy=vot∙sinα – gt2/2. (2)
В верхней точке vy=0 и из (1) получим vo∙sin𝛼 = gt1, отсюда время подъема мяча t1=vo∙sinα/g. Подставляя t1 в (2), получим
sy max= vo2 ∙sin2α/(2g)= 2,1 м.
2) Найдем дальность полета sx max тела, брошенного под углом к горизонту.
Имеем: vx=vo∙cosα, (3)
sx=vxt=vot∙cosα.(4)
Тело упадет на горизонтальную плоскость через время t2=2t1=2vosinα/g.
Подставляя t2 в (4), получим sxmax = vо2sin2α/g=10,0 м.
3) t2=2t1=2vosinα/g=1,3 с.
Пример 19.Тело брошено со скоростью v0=10 м/с2 под углом α=30° к горизонту. На какую высоту тело поднимется. На каком расстоянии от места бросания оно упадет на землю? Какое время он будет в движении?
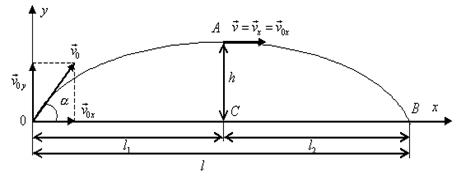
Решение.Горизонтальная и вертикальная составляющие начальной скорости
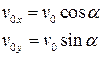
Движение на участке ОА можно разложить на два простых движения: равномерное по горизонтали и равнозамедленное по вертикали:
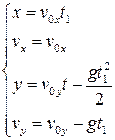
В точке А
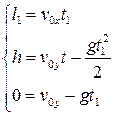
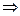
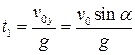 .
.
Тогда 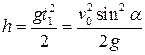 и
и 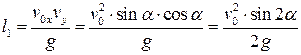 .
.
Если тело участвует одновременно в нескольких движениях, то в каждом из них оно участвует независимо от другого, следовательно, время движения на участке АВ определяется временем движения вниз – t2. На основании вывода, сделанного в задаче 4, время движения вверх равно времени движения вниз, а, значит, 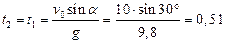 с
с 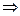
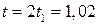 с.
с.
При равномерном движении по горизонтали за равные промежутки времени тело проходит равные участки пути, следовательно,
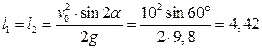 м.
м.
Дальность полета 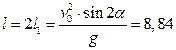 м.
м.
Высота подъема тела 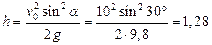 м.
м.
Пример 20.Точка движется прямолинейно на плоскости по закону x=4(t-2)2. Каковы начальная скорость v0 и ускорение точки a? Найти мгновенную скорость точки vt=5 в начале пятой секунды движения.
Решение.
1) Т.к. 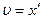 , то
, то 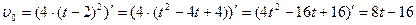
при 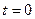
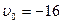 м/с.
м/с.
2) Т.к. 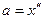 , то
, то 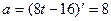 м/с.
м/с.
3) При t=4, т.к. до начала 5 с прошло 4 с.
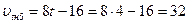 м/с.
м/с.
Ответ: Начальная скорость точки v0=-16 м/с, ускорение a=8 м/с, скорость точки в начале пятой секунды движения vt=5=32 м/с.
Вопросы для самопроверки
- Что изучает кинематика?
- Совпадает ли направление ускорения с направлением скорости материальной точки при равноускоренном движении? при равнозамедленном движении?
- Какие кинематические характеристики движения остаются постоянными при равномерном прямолинейном движении? при равноускоренном движении?
- Какие величины, характеризующие движение, можно определить по графику скорости?
- Два поезда идут навстречу друг другу; один ускоренно на север, другой замедленно на юг. Как будут направлены векторы ускорений поездов?
- Чем отличаются движения, уравнения которых приведены x1=3-5t-2t2; x2=-3+5t-2t2 ?
- Какие существуют способы описания движения материальной точки?
- Перечислите основные способы задания движения точки.
- Что должно быть известно при естественном способе задания движения точки?
- Какие кинематические способы задания движения точки существуют и в чем состоит каждый из этих способов?
- Запишите в общем виде закон движения в естественной и координатной форме?
- Что называют траекторией движения?
- Как определяется скорость движения при естественном способе задания движения?
- Запишите формулы для определения касательного, нормального и полного ускорений?
- Что характеризует касательное ускорение и как оно направлено по отношению к вектору скорости?
- Что характеризует нормальное ускорение и как направлено нормальное ускорение?
