Каковы особенности работы схемы тактовой синхронизации?

Ход работы

Для выполнения лабораторной работы запустили среду MATLAB.

Создали новый Blank M-File и ввели туда код, значения переменных выбирали согласно своему варианту.

Таблица №1 – значения своего варианта

Вариант	Тип модуляции	Фактор скругления rollof	Скорость передачи (бит/с) br	Коэффициент r	Разность несущих частот, Гц
	‘QAM8’	0,4		0.67	16.3977

Рассчитали частоту несущей по следующей формуле:

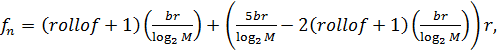(1)

М-количество точек в сигнальном созвездии (для QPSK М=4)

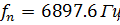
Задали разность несущих частот в соответствии с вариантом:

df = 16.3977

После того как в код введены данные своего варианта, запустили программу.

clear; clc; close all;

modulation = QAM8;

M = 8;

rollof = 0.4;

br = 7200;

fn = 6897.6;

start = 3;

distance = 1;

n = 10000;

tz = 0.7;

df = 16.3977;

z = 1;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

bor = br/log2(M);

fd = bor*10;

delay = 20*log2(M);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

data = m_source( n,8 );

[ a ] = qam_mapper( data,'modulate',modulation );

I = a(1,:);

Q = a(2,:);

[ no_care ] = IQ_plot( I,Q );

[ I ] = interp( I,10 );

[ Q ] = interp( Q,10 );

[ I ] = r_cos_fir( I,rollof,10,'sqrt',fd,bor );

[ Q ] = r_cos_fir( Q,rollof,10,'sqrt',fd,bor );

[ s ] = IQ_mod_synhr( I,Q,fn,fd,tz,df );

no_care = spectrum_analyzer( s,fd,'Blackman','real','normal' );

[ noisy_s ] = radio_channel( s, distance );

[ Ir,Qr,fin,fi ] = IQ_demod_synhr( noisy_s,fn,fd,tz,0.001 );

[ Ir ] = r_cos_fir( Ir,rollof,10,'norm_sqrt',fd,bor );

[ Qr ] = r_cos_fir( Qr,rollof,10,'norm_sqrt',fd,bor );

[ no_care ] = eye_diagram( Ir,10,1,1,1000 );

[ Ir,Qr ] = clock_synchr( Ir,Qr,bor,10,z );

[ no_care ] = IQ_plot( Ir*2,Qr*2 );

out(1,:) = Ir*2;

out(2,:) = Qr*2;

[ data_out ] = qam_mapper( out,'demodulate',modulation );

[ ber,pos ] = m_compare( data_out,8,0.3 );

disp(ber);

Меняя порядок фильтра в цепи тактовой синхронизации (переменная z) в диапазоне от 1 до 100 согласно таблице 2, провели 6 замеров вероятности битовой ошибки для 10 значений distance в диапазоне от d_min до d_max. Длительность отрезка немодулированной несущей установим равной t_z=1. Полученные результаты запишем в таблицы 3-17.

Таблица 2 – порядки фильтров в экспериментах

Эксперимент

Порядок

Таблица 3 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=1.

distance	dmin									dmax
	0,1631	0,1597	0,176	0,1872	0,1953	0,2019	0,212	0,2244	0,2347	0,2432
	0,1587	0,1683	0,1776	0,1894	0,1895	0,2029	0,2184	0,2245	0,2394	0,2385
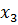	0,1619	0,1728	0,1737	0,1894	0,1985	0,2004	0,2229	0,2316	0,2359	0,23
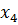	0,1606	0,1641	0,1761	0,1807	0,1932	0,2014	0,2076	0,2229	0,2366	0,2334
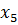	0,1614	0,1684	0,1819	0,1866	0,1952	0,2033	0,2129	0,2265	0,2226	0,2418
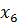	0,1624	0,1748	0,1761	0,1842	0,1939	0,2115	0,2159	0,2205	0,2292	0,2324
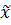	0,1614	0,1680	0,1769	0,1863	0,1943	0,2036	0,2150	0,2251	0,2331	0,2366
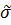	0,0006	0,0023	0,0011	0,0014	0,0012	0,0016	0,0022	0,0015	0,0025	0,0022
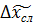	0,0025	0,0091	0,0045	0,0055	0,0048	0,0066	0,0087	0,0062	0,0100	0,0088

Таблица 4 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=3.

distance	dmin									dmax
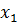	0,1212	0,1328	0,1275	0,148	0,1498	0,1625	0,1764	0,1852	0,1939	0,2129
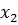	0,1218	0,1281	0,1397	0,1393	0,1603	0,1671	0,1775	0,1836	0,1913	0,2077
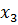	0,1213	0,1291	0,1351	0,1377	0,1481	0,1636	0,1684	0,188	0,1918	0,2075
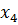	0,1213	0,1265	0,1379	0,1423	0,1533	0,1676	0,1686	0,1914	0,1926	0,208
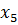	0,1228	0,1321	0,1327	0,1366	0,1459	0,1606	0,1807	0,1826	0,1937	0,2236
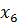	0,1251	0,1277	0,1376	0,14	0,1521	0,1635	0,1783	0,185	0,2049	0,2032
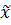	0,1223	0,1294	0,1351	0,1407	0,1516	0,1642	0,1750	0,1860	0,1947	0,2105
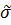	0,0006	0,0010	0,0018	0,0017	0,0021	0,0011	0,0021	0,0013	0,0021	0,0029
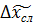	0,0025	0,0041	0,0073	0,0067	0,0082	0,0044	0,0085	0,0053	0,0083	0,0116

Таблица 5 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=7.

distance	dmin									dmax
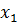	0,0566	0,0628	0,0667	0,0804	0,0902	0,1115	0,1257	0,1399	0,154	0,1736
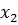	0,0535	0,0606	0,0658	0,0852	0,0927	0,114	0,1271	0,135	0,1501	0,1632
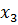	0,0589	0,0598	0,0748	0,0897	0,0875	0,1113	0,1272	0,141	0,1554	0,1653
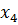	0,0568	0,0653	0,0697	0,0801	0,0901	0,107	0,1257	0,1338	0,1524	0,1774
	0,0525	0,0587	0,0742	0,0875	0,0927	0,1135	0,118	0,1305	0,1515	0,1735
	0,0582	0,0634	0,0707	0,0832	0,0952	0,1102	0,1305	0,1382	0,15	0,1728
	0,0561	0,0618	0,0703	0,0844	0,0914	0,1113	0,1257	0,1364	0,1522	0,1710
	0,0010	0,0010	0,0015	0,0016	0,0011	0,0010	0,0017	0,0016	0,0009	0,0022
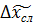	0,0042	0,0041	0,0061	0,0063	0,0044	0,0041	0,0068	0,0065	0,0035	0,0090

Таблица 6 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=10.

distance	dmin									dmax
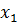	0,0117	0,0202	0,0325	0,0469	0,0611	0,0739	0,0888	0,1174	0,1307	0,1512
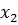	0,0128	0,0198	0,0302	0,0445	0,057	0,0755	0,098	0,1111	0,1227	0,1427
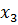	0,0158	0,0201	0,0347	0,0463	0,0634	0,0695	0,0886	0,1079	0,1265	0,1439
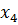	0,0128	0,0164	0,0344	0,0443	0,0561	0,0752	0,0905	0,1036	0,1286	0,1582
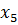	0,0146	0,0217	0,0291	0,0393	0,0615	0,0754	0,0978	0,1163	0,1267	0,1438
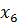	0,0155	0,0222	0,0334	0,0446	0,0575	0,0804	0,0833	0,1044	0,1256	0,1433
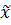	0,0139	0,0201	0,0324	0,0443	0,0594	0,0750	0,0912	0,1101	0,1268	0,1472
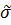	0,0007	0,0008	0,0009	0,0011	0,0012	0,0014	0,0023	0,0024	0,0011	0,0025
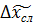	0,0027	0,0033	0,0037	0,0044	0,0048	0,0057	0,0094	0,0096	0,0044	0,0102

Таблица 7 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=15.

distance	dmin									dmax
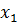	0,0029	0,0061	0,0108	0,0251	0,0388	0,0581	0,0649	0,0873	0,111	0,1306
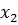	0,0023	0,0065	0,0127	0,0259	0,0378	0,05	0,0725	0,0891	0,1087	0,1306
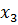	0,0015	0,0059	0,0132	0,0265	0,0385	0,0546	0,0688	0,0861	0,1054	0,1243
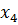	0,0032	0,0049	0,0144	0,0267	0,0373	0,0469	0,0674	0,0849	0,1088	0,1274
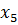	0,0021	0,007	0,0181	0,0241	0,0385	0,0549	0,066	0,0905	0,0965	0,1279
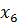	0,0037	0,0068	0,0134	0,0259	0,0374	0,0588	0,0679	0,0856	0,1114	0,1259
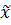	0,0026	0,0062	0,0138	0,0257	0,0381	0,0539	0,0679	0,0873	0,1070	0,1278
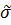	0,0003	0,0003	0,0010	0,0004	0,0003	0,0019	0,0011	0,0009	0,0023	0,0010
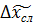	0,0013	0,0012	0,0040	0,0016	0,0010	0,0076	0,0043	0,0035	0,0091	0,0041

Таблица 8 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=20.

distance	dmin									dmax
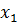	0,0015	0,0059	0,0086	0,0236	0,033	0,0512	0,0642	0,0816	0,0975	0,1203
	0,0016	0,0072	0,0095	0,0212	0,0348	0,0549	0,067	0,0792	0,098	0,1204
	0,0011	0,0038	0,0092	0,0218	0,0303	0,055	0,0652	0,0814	0,095	0,1164
	0,0019	0,0042	0,0136	0,0237	0,0333	0,0515	0,0639	0,0804	0,0883	0,128
	0,0007	0,006	0,0105	0,0256	0,0282	0,0498	0,0623	0,081	0,0973	0,1189
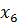	0,0014	0,0054	0,0111	0,0222	0,032	0,0494	0,0581	0,0809	0,0958	0,1227
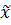	0,0014	0,0054	0,0104	0,0230	0,0319	0,0520	0,0635	0,0808	0,0953	0,1211
	0,0002	0,0005	0,0007	0,0007	0,0010	0,0010	0,0012	0,0004	0,0015	0,0016
	0,0007	0,0020	0,0029	0,0026	0,0039	0,0040	0,0050	0,0014	0,0059	0,0065

Таблица 9 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=25.

distance	dmin									dmax
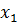	0,0017	0,0045	0,0098	0,0237	0,0292	0,0492	0,0654	0,0844	0,0925	0,1166
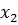	0,0014	0,0044	0,0122	0,017	0,0341	0,0519	0,0588	0,0762	0,0967	0,121
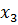	0,0019	0,0051	0,0109	0,0193	0,033	0,045	0,0591	0,0832	0,1006	0,1178
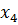	0,0009	0,0067	0,0084	0,0266	0,0301	0,0465	0,0622	0,0734	0,0936	0,1207
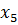	0,001	0,0045	0,0102	0,0208	0,0339	0,0466	0,0592	0,0769	0,0939	0,121
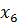	0,0014	0,0064	0,0089	0,021	0,0265	0,0482	0,065	0,0819	0,0902	0,1145
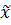	0,0014	0,0053	0,0101	0,0214	0,0311	0,0479	0,0616	0,0793	0,0946	0,1186
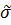	0,0002	0,0004	0,0006	0,0014	0,0012	0,0010	0,0012	0,0018	0,0015	0,0011
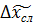	0,0006	0,0017	0,0022	0,0055	0,0050	0,0040	0,0050	0,0072	0,0059	0,0045

Таблица 10 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=30.

distance	dmin									dmax
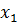	0,0012	0,0043	0,0087	0,0171	0,0288	0,0407	0,0662	0,0758	0,0891	0,1112
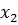	0,0016	0,0047	0,0097	0,0173	0,0326	0,0482	0,0617	0,0746	0,0906	0,1068
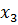	0,0017	0,0041	0,0122	0,0229	0,0287	0,0467	0,0616	0,0803	0,0933	0,117
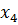	0,0017	0,0047	0,0124	0,0187	0,0292	0,0441	0,0638	0,0832	0,0948	0,1184
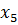	0,0018	0,0034	0,0122	0,0228	0,0312	0,0449	0,0614	0,0746	0,0906	0,1075
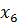	0,0017	0,0048	0,0134	0,0191	0,0348	0,0457	0,0616	0,0761	0,0955	0,1167
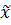	0,0016	0,0043	0,0114	0,0197	0,0309	0,0451	0,0627	0,0774	0,0923	0,1129
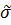	0,0001	0,0002	0,0007	0,0011	0,0010	0,0010	0,0008	0,0014	0,0011	0,0021
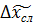	0,0003	0,0009	0,0030	0,0042	0,0040	0,0042	0,0031	0,0057	0,0042	0,0084

Таблица 11 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=40.

distance	dmin									dmax
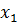	0,001	0,0063	0,0079	0,0196	0,033	0,0425	0,0651	0,0764	0,0914	0,0874
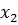	0,0006	0,0039	0,0068	0,0202	0,0262	0,0419	0,0637	0,0792	0,0937	0,1044
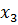	0,0022	0,0049	0,0112	0,0208	0,0339	0,0424	0,0609	0,0782	0,0921	0,1127
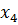	0,0019	0,0038	0,0081	0,0188	0,0265	0,0434	0,0602	0,0775	0,0891	0,1159
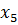	0,0007	0,0038	0,0077	0,0201	0,0259	0,0478	0,0555	0,0754	0,0887	0,1117
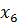	0,0004	0,0035	0,011	0,0196	0,0323	0,0444	0,0619	0,0823	0,0918	0,1135
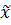	0,0011	0,0044	0,0088	0,0199	0,0296	0,0437	0,0612	0,0782	0,0911	0,1076
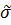	0,0003	0,0004	0,0008	0,0003	0,0016	0,0009	0,0014	0,0010	0,0008	0,0043
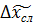	0,0012	0,0017	0,0030	0,0011	0,0062	0,0036	0,0054	0,0040	0,0031	0,0174

Таблица 12 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=50.

distance	dmin									dmax
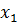	0,0008	0,0034	0,0102	0,0189	0,032	0,0446	0,0559	0,0745	0,0834	0,1108
	0,0001	0,0058	0,0095	0,0174	0,0315	0,05	0,0494	0,0819	0,0987	0,109
	0,001	0,0046	0,0089	0,0189	0,0293	0,0415	0,0548	0,0787	0,096	0,1154
	0,0007	0,003	0,0102	0,0175	0,0256	0,0475	0,0606	0,0779	0,0886	0,1075
	0,0006	0,0034	0,0087	0,0177	0,0274	0,047	0,0647	0,0776	0,0941	0,1137
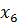	0,0015	0,0029	0,012	0,0157	0,0286	0,0414	0,061	0,0801	0,0872	0,1063
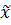	0,0008	0,0039	0,0099	0,0177	0,0291	0,0453	0,0577	0,0785	0,0913	0,1105
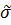	0,0002	0,0005	0,0005	0,0005	0,0010	0,0014	0,0022	0,0010	0,0024	0,0015
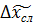	0,0008	0,0018	0,0020	0,0019	0,0040	0,0057	0,0089	0,0041	0,0096	0,0058

Таблица 13 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=60.

distance	dmin									dmax
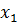	0,001	0,0041	0,0095	0,018	0,0305	0,0452	0,0563	0,0762	0,0894	0,1081
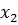	0,0004	0,0042	0,0065	0,0173	0,0242	0,0434	0,0574	0,0733	0,0931	0,1126
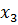	0,0023	0,0045	0,0106	0,018	0,029	0,0427	0,0604	0,0771	0,0897	0,1093
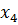	0,0004	0,004	0,0125	0,0184	0,0285	0,0437	0,0511	0,0721	0,1087	0,118
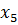	0,0005	0,0046	0,0119	0,0195	0,0291	0,0421	0,0609	0,0742	0,0979	0,1089
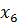	0,0009	0,0027	0,0079	0,0177	0,0302	0,0439	0,0586	0,0741	0,0904	0,1189
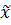	0,0009	0,0040	0,0098	0,0182	0,0286	0,0435	0,0575	0,0745	0,0949	0,1126
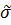	0,0003	0,0003	0,0009	0,0003	0,0009	0,0004	0,0015	0,0008	0,0031	0,0019
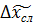	0,0012	0,0011	0,0038	0,0012	0,0037	0,0017	0,0058	0,0030	0,0122	0,0078

Таблица 14 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=70.

distance	dmin									dmax
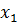	0,0007	0,0052	0,0084	0,0177	0,0275	0,0397	0,0664	0,0697	0,0895	0,1064
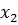	0,0007	0,004	0,0081	0,023	0,0325	0,0378	0,0566	0,0689	0,0863	0,0987
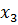	0,0011	0,0033	0,009	0,0182	0,0295	0,0401	0,0549	0,0791	0,0925	0,1035
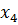	0,0006	0,004	0,0084	0,0167	0,0338	0,0468	0,0575	0,0733	0,0883	0,105
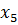	0,001	0,0037	0,0112	0,0182	0,0277	0,0412	0,0601	0,0709	0,0911	0,1151
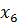	0,0007	0,0027	0,0086	0,0227	0,0278	0,0397	0,0596	0,0727	0,0908	0,106
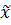	0,0008	0,0038	0,0090	0,0194	0,0298	0,0409	0,0592	0,0724	0,0898	0,1058
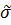	0,0001	0,0003	0,0005	0,0011	0,0011	0,0013	0,0016	0,0015	0,0009	0,0022
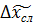	0,0003	0,0014	0,0019	0,0044	0,0044	0,0051	0,0066	0,0060	0,0036	0,0087

Таблица 15 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=80.

distance	dmin									dmax
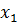	0,0012	0,0039	0,0088	0,0153	0,0321	0,0424	0,0573	0,071	0,0878	0,1164
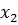	0,0008	0,0034	0,011	0,0204	0,0301	0,0436	0,058	0,068	0,0873	0,109
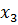	0,0005	0,004	0,0084	0,0167	0,0281	0,0409	0,0591	0,0799	0,0982	0,1119
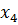	0,001	0,0033	0,013	0,0218	0,0296	0,045	0,0601	0,069	0,0935	0,1163
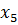	0,0008	0,0029	0,01	0,0188	0,0255	0,0447	0,054	0,0739	0,0842	0,1087
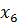	0,0002	0,003	0,007	0,0146	0,0231	0,0405	0,0595	0,0772	0,0859	0,1192
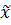	0,0008	0,0034	0,0097	0,0179	0,0281	0,0429	0,0580	0,0732	0,0895	0,1136
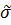	0,0001	0,0002	0,0009	0,0012	0,0013	0,0008	0,0009	0,0019	0,0022	0,0018
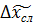	0,0006	0,0007	0,0035	0,0047	0,0054	0,0031	0,0036	0,0077	0,0087	0,0071

Таблица 16 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=90.

distance	dmin									dmax
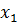	0,0016	0,0046	0,0077	0,0194	0,0285	0,0425	0,0604	0,0718	0,0882	0,1139
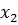	0,0016	0,0035	0,0086	0,0192	0,0274	0,0403	0,0662	0,0733	0,0911	0,1046
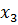	0,0011	0,0037	0,008	0,0176	0,0254	0,04	0,0613	0,0698	0,0848	0,1129
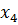	0,0009	0,0025	0,0079	0,0191	0,0293	0,04	0,0615	0,0782	0,0898	0,1077
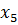	0,001	0,0043	0,0094	0,0193	0,0279	0,0375	0,058	0,0713	0,0936	0,1186
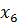	0,0007	0,004	0,0079	0,0203	0,0285	0,0406	0,0638	0,0722	0,0881	0,1084
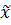	0,0012	0,0038	0,0083	0,0192	0,0278	0,0402	0,0619	0,0728	0,0893	0,1110
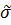	0,0002	0,0003	0,0003	0,0004	0,0006	0,0007	0,0012	0,0012	0,0012	0,0021
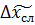	0,0006	0,0012	0,0010	0,0014	0,0022	0,0026	0,0046	0,0047	0,0049	0,0083

Таблица 17 – 6 замеров вероятности битовой ошибки для 10 значений переменной distance при z=100.

distance	dmin									dmax
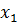	0,0012	0,0032	0,0114	0,0167	0,0269	0,0419	0,0565	0,0735	0,0925	0,1117
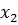	0,001	0,0039	0,007	0,0197	0,0302	0,0456	0,0572	0,0693	0,0922	0,1003
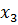	0,001	0,0029	0,0072	0,0193	0,0335	0,0442	0,0608	0,0684	0,0876	0,1124
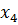	0,0009	0,0033	0,0069	0,0209	0,0275	0,0442	0,0574	0,0791	0,084	0,1139
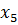	0,0018	0,0031	0,0101	0,0174	0,0307	0,043	0,0582	0,0723	0,0832	0,1107
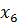	0,0013	0,0023	0,0089	0,0154	0,0287	0,0378	0,0583	0,0708	0,085	0,1099
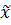	0,0012	0,0031	0,0086	0,0182	0,0296	0,0428	0,0581	0,0722	0,0874	0,1098
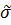	0,0001	0,0002	0,0008	0,0008	0,0010	0,0011	0,0006	0,0016	0,0017	0,0020
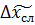	0,0005	0,0009	0,0031	0,0034	0,0040	0,0045	0,0024	0,0063	0,0067	0,0079

Построим график зависимости вероятности ошибки от дальности связи, без доверительного интервала, для всех порядков фильтра в цепи синхронизации на одной плоскости.

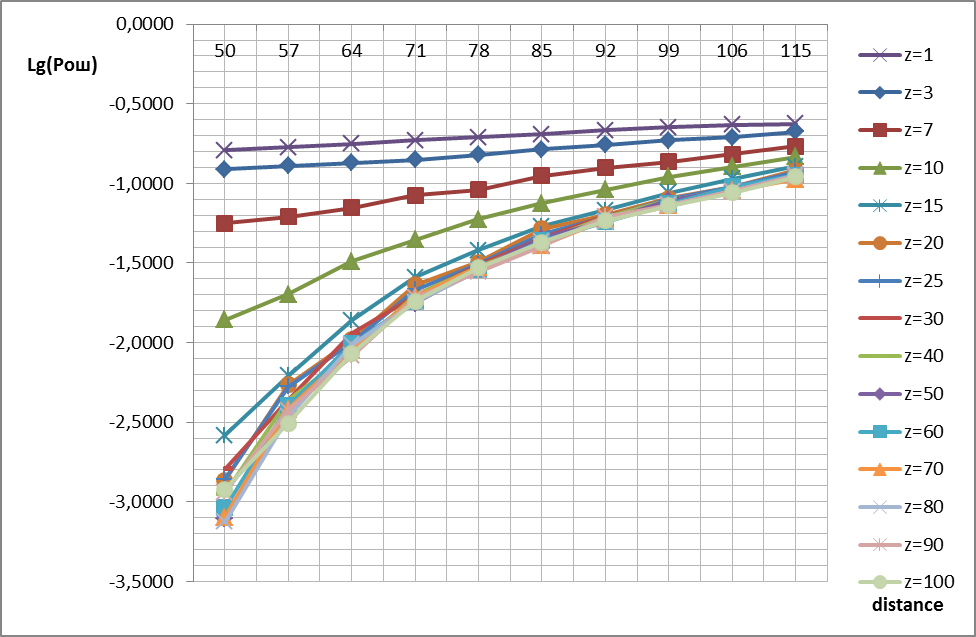
Рис.1 – График зависимости вероятности ошибки от дальности связи

Основным показателем качества функционирования цифровых систем связи является вероятность битовой ошибки. Таким образом, выберем порядок фильтра в цепи синхронизации, при котором обеспечивается минимальная вероятность битовой ошибки. Но при этом стоит учитывать, что порядок фильтра на практике чем меньше, тем лучше. На рисунке 1 можно увидеть, что оптимальной зависимостью будет кривая при z=60.

Дополним график лабораторной работы №1.

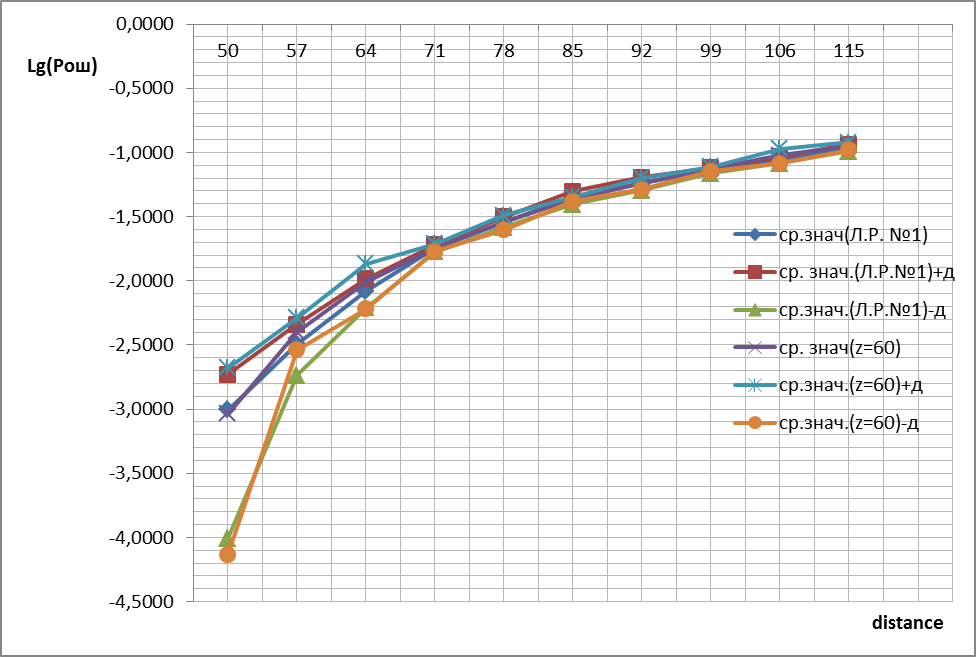
Рис. 2 – График зависимости вероятности ошибки от дальности связи с доверительным интервалом при частотном рассогласовании по несущей и тактовой частотам и график из лабораторной работы №1

Вывод:

Проанализировав график на рисунке 2 можно сказать, что при рассогласовании по несущей и тактовой частотам вероятность битовой ошибки выше, чем для случая с идеальной синхронизацией, но не значительно. Также видно, что ошибка приближается к значениям, полученным в 1 лабораторной работе, следовательно, помехоустойчивость при тактовой синхронизации модема близка к идеальной.

Контрольные вопросы

Каковы особенности работы схемы тактовой синхронизации?

Схема тактовой (символьной) синхронизации (СТС) формирует на выходе последовательность периодических импульсов, совпадающих по времени с моментами окончания 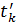импульсов принимаемых кодовых комбинаций. В большинстве радиосистем синхронизация осуществляется по информационному сигналу, и в некоторых случаях для вхождения СТС в режим синхронизма передается специальный синхросигнал. Синхронизация с использованием информационного сигнала имеет ряд особенностей, которые определяют алгоритмы обработки сигналов и принципы построения СТС.

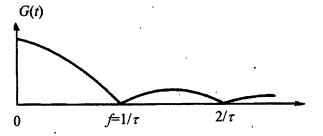
Рис. 3 – фрагмент спектра принимаемого сигнала

Схема тактовой синхронизации в режиме слежения должна постоянно измерять частоту и фазу следования импульсов принимаемой кодовой комбинации. Если принимается двоичная непрерывная последовательность импульсов, каждый из которых имеет длительность τ, то СТС должна выделить и обработать гармонику 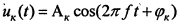с частотой f = 1/τ.

Первая особенность этой схемы заключается в том, что в спектре достаточно протяженной последовательности двоичных равновероятных символов (рис. 3), гармоника с частотой f = 1/τ отсутствует, и ее необходимо восстанавливать в СТС. Аналогичный эффект сопровождает работу схемы синхронизации по несущей.

Вторая особенность связана с тем, что на вход СТС в некоторые интервалы времени могут поступать последовательности импульсов одинаковой полярности: положительной или отрицательной. Эти интервалы, в течение которых на вход СТС действует фактически постоянная составляющая, непродолжительны, однако достаточны, чтобы СТС вышла из режима синхронизма. Схемы тактовой синхронизации в режиме слежения можно разделить на два принципиально различающихся типа:

1) СТС с нелинейной обработкой, применяемая в радиосистемах с высокой скоростью передачи информации при больших значениях отношения сигнал/шум;

2) «синфазно-среднефазная» схема синхронизации, которая может быть использована при малых значениях отношения сигнал/шум. Схема устойчиво работает при наличии относительно продолжительных интервалов времени приема импульсов одинаковой полярности.