Влияние ошибок счислимых кординат на вычисляемый азимут. Выгодные условия наблюдений.

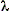Для вычисления азимута необходимо использовать координаты места судна, которые как правило, являются счислимыми. Азимут, вычесленный по счислимым координатам, также будет счислимым А_с. Для получения поправки компаса требуется истинный азимут светила А_и. Погрешности в счислимых координатах и вызывают погрешность в азимуте А = А + А 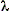, которая входит в поправку компаса.
Определим, при каких условиях погрешностями А и А 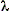можно пренебречь.

Погрешность в А вызвана погрешностью в широте.
Погрешность в азимуте за широту определяется на основе дифференциальных формул мореходной астрономии.

A = tghsinA (1.6)

Анализируя эту фомулу, приходим к следующему выводам.

Чтобы минимизировть погрешность A и получить точную поправку компаса необходимо:

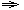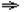• пеленговать светило на малой высоте (если h 0, то A 0.
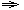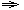• если над горизонтом висит облачность и нельзя выбрать светило с малой высотой, но существует возможность выбора светил (ночное время - много ярких звезд), то следует пеленговать светило вблизи меридиана наблюдателя, т.к. если А 0° (180°), то A 0.

В северном полушарии по второй причине в этом случае является Полярная звезда (её азимут близок к 0°).

Погрешность в А, вызванная погрешностью в долготе.
Долгота входит в расчет местного часового угла t_м = t_гр ± 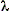^E_W. Гринвичский часовой угол определён точно, поэтому погрешность часового угла будет полностью определяться погрешностью в долготе t = 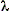. Следовательно, используя основые дифференциальную формулы мореходной строномии, имеем

A _t = -cosqcosqsech t (1.8)

Анализируя эту фомулу, приходим к следующему выводам.

1. Погрешность в А 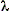зависит от высоты светила и будут меньше при его малой высоте. Т.е. необходимо пеленговать светила на малой высоте.

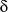
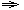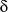
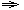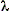
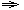2. При пеленговании приполярных светил (если 90°, то cos 0) погрешность в А 0.
Таким идеальным светилом является Полярная звезда.

В заключении отметим еще один факт. На точность поправки компаса влияет не только погрешности ИП, которые мы уже расмотрели, но и погрешности в самом гирокомпасном пеленге ГКП. Погрешность ГКП также зависит от высоты пеленгуемого светила и определяется следующим выражением:

А = ktgh (3.1)

k - угол наклона пеленгатора.
Следовательно, для точного взятия гирокомпасного пеленга (и для точного определения поправки компаса) необходимо пеленговать светило на малой высоте.

Определение поправки компаса методом моментов.

· Теория метода.

· Порядок наблюдений.

· Порядок вычислений.

· Достоинства и недостатки метода.

Теория метода.

Метод моментов получил свое название, потому что в момент пеленгования светила фиксируется гринвичское время, т.е. момент времени.

Т.е. измерения дают нам два параметра: гирокомпасный пеленг - ГКП и гринвичское время - Т_гр. Далее с карты снимаются счислимые координаты _с, _с. По гринвичскому времени по МАЕ вычисляется местный часовой угол t_м и склонение светила .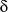
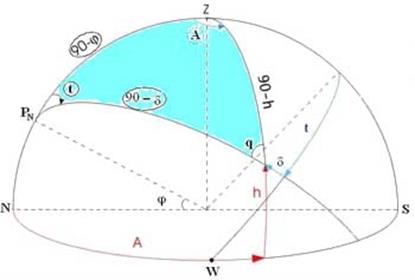
Применив формулу котангенсов к параллактическому треугольнику P_NZC, выведем формулу

ctgA = cos tg 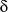cosect - sin ctgt (1.2)

(Подробный вывод этой формулы есть в параграфе "Параллактический треугольник и его решение".)

По данной формуле азимут получается в полукруговом счете.
Первая буква одноименна с широтой, вторая буква одноименна с часовым углом.
Азимуты по таблицам ВАС-58 вычисляются по данной формуле. Из табличных методов определения поправки компаса таблицы ВАС-58 являются наиболее удобными.

Порядок наблюдений.

Порядок наблюдений покажем на следующем примере.
24-го марта 2001 года на вахте 16^ч - 20^ч необходимо определить поправку компаса.
Выбрать светило как можно ближе к горизонту. В данном случае это будет Солнце перед заходом.
Взять пеленг светила. В момент взятия пеленга запустить секундомер.

ГКП = 264,6°

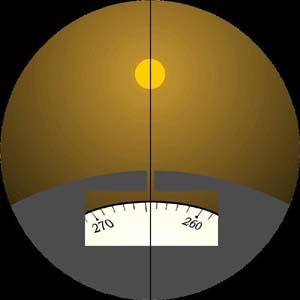
В штурманской рубке выполнить следующие действия.
По приемоиндикатору остановить секундомер и записать:
Гринвичское время в момент остановки секундомера и показания секундомера.

Т_{гр.ост.сек}= 19^ч42^м55^с
Т_{ост.сек}=0^м50^с.

Судовое время и ОЛ.

Т_с = 19^ч42^м

По ОЛ с карты (или с приемоиндикатора) снять счислимые координаты.
= 21°45,6'S; = 33°14,6'W.

Порядок вычислений.

Найти приближенное гринвичское время и гринвичскую дату.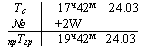
Найти точное гринвичское время и по МАЕ на данное время рассчитать местный часовой угол и склонение светила.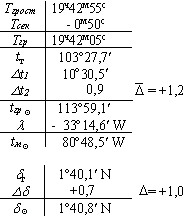
Войти в таблицы ВАС-58 по аргументам и найти азимут в полукруговом счете.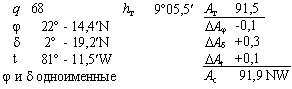
Перевести азимут в круговой счет.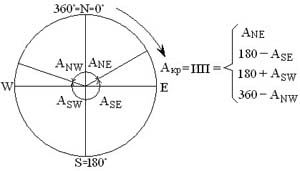
Найти поправку компаса

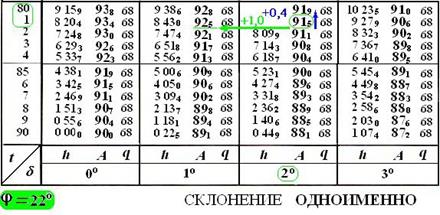
Напоминаем, что при расчете азимута поправка азимута за часовой угол находится путем интерполирования из основных таблиц.
A_t = +0,4°х(11,5/60)=+0.1.
Поправка азимута за склонение выбирается из таблицы 1 по аргументам 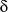и q, а знак определяется из основных таблиц путем сравнения двух азимутов, расположенных в двух соседних колонках склонений в 2° и 1°. Но если склонение светила < 29° (для Солнца, Луны и планет), то шаг по склонению составляет 1°, поэтому поправку азимута за склонение можно выбрать по основным таблицам. A 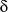= +1,0°х(19,2/60) = +0,3°.
При определении поправки компаса пеленгуют светило на малой высоте. Тогда, согласно формуле A = tghsinA поправка не превосходит 0,1°, а чаще всего она равняется нулю. Поэтому при малых высотах можно данной поправкой пренебречь. Это был рассмотрен рациональный способ определения поправки компаса по таблицам ВАС-58.