Кеңею кезіндегі кванттық флуктуациялар

Қара тесік пен де Ситтер дүниесі арасындағы аналогия кеңейген кезде кванттық әсерлерді зерделегенде де пайдалы. Мысалы, Хоукинг температурасымен сәуле шығара отырып, қара тесіктің буланатындығы белгілі, мұнда М - қара тесіктің салмағы [119]. Мұнда бақылаушы өзін температурасы бар «жылу моншасында» жүргендей сезінетін болатын осы тәріздес құбылыс де Ситтер дүниесінде де бар. Сөз жүзінде, бұған де Ситтер дүниесіндегі өрістің кванттық теориясының евклидтік тұжырымдамасына көшу үшін, (7.2.5) формулада t ® iτ алмастыру жасап көз жеткізуге болады. Метрика бұл кезде S⁴ сферасының метрикасының түрін алады:

. (7.3.1)

Сферадағы бозе-өрістер 2p/Н кезеңмен τ бойынша мерзімді, бұл Т_Н = Н/2p [201] температура кезінде кванттық статистиканы қарастыруға эквивалентті [201]. Физикалық тұрғыдан, де Ситтер дүниесінде Т_Н температураның пайда болуы (қара тесікпен жағдайдағы секілді) оқиғалар көкжиегінің болуымен және көкжиектің артындағы жағдайлар бойынша орташаландыру енгізу қажеттілігімен байланысты [119, 120]. Алайда, де Ситтер дүниесінің «температурасы» аса әдеттен өзгеше.

Істің мәнісі S⁴ евклидтік сфераның барлық төрт бағыт бойынша мерзімді екендігінде. Сондықтан вакуумдық флуктуациялардың спектрі планктіктен аса алыс болып шығады.

Біз үшін одан арғы жерде немесе типті орташаларын зерделеу әсіресе маңызды болады. Минковский кеңістігінде нөлдік емес температура кезінде

бұл n бойынша жиынтықты есептегеннен кейін (j₂) үшін (3.1.7) өрнекке алып келеді. S⁴ кеңістікте барлық интегралдаулардың орнына n_i, i = 1, 2, 3, 4 бойынша жиынтықтау, ал температураның орнына Н/2p шамасы пайда болады. n_i бойынша жиынтықта ерекше маңыздылықты m² ® о кезінде (j₂) көш бастайтын үлесті беретін n_i = 0 мүше ойнайды. Бұл үлестің Н4/ m² – ге пропорционал екендігін түсіну қиын емес. Бұл үлесті есептеу m² << Н² кезінде (j₂) үшін келесі өрнекке (бастапқыда басқа тәсіл бойынша алынған) алып келеді [202, 126-128]:

(7.3.3)

m² ® о кезіндегі (j₂) шамасының патологиялық жүріс-тұрысы өзіне назар аударады. Формалды себеп тап осы бір жиынтықтаудың орнына біздің енді төрт жиынтықтауды алатындығымыздан және де Ситтер дүниесіндегі скалярлы өріс теориясындағы тиісті инфрақызыл жиынтықталмаулардың кванттық статистикадағыға қарағанда үш ретке күшті болып шығатындығынан тұрады¹). Одан арғы жерде осыншама таң қаларлық нәтиженің пайда болуының физикалық себебін түсіну өте маңызды.

Осы мақсатпен бұл Минковский дүниесінде жүргізілген тәрізді, (7.2.3) координаталарда де Ситтер дүниесінде салмақсыз j скалярлы өрісін кванттауды жүргіземіз [202, 126-128]. j (х) скалярлы өрістің операторын мынандай түрде көрсетуге болады:

(7.3.4)

мұнда, (1.7.13) сәйкес, Ψ_ρ (t) функциялары теңдеуді қанағаттандырады.

. (7.3.5)

¹) Векторлық немесе спинорлық өрістер теориясында n_i бойынша жиынтықтардың m ® О кезінде жиынтықталмаулар пайда болмайтындай етіп құрылғандығын атай кетейік.

Минковский дүниесінде Ψ_ρ (t) функциясының рөлін келесі функция ойнады: , мұнда , (1.1.3) қар. Де Ситтер дүниесінде (7.2.3) жалпы теңдеудің (7.3.5) шешімі мынандай түрге ие:

, (7.3.6)

мұнда η – конформдық уақыт: η = - Ганкель функциялары;

. (7.3.7)

Жоғары жиіліктер шегнде де Ситтер дүниесінде кванттау және Минковский дүниесінде кванттау өзгешеленбеуге тиіс, яғни с₁ (р) ® О, с₂ (р) ® -1 кезінде р ® ∞. Бұл шарт, жекелей алғанда, с₁ = 0, с₂ = -1 кезінде орындалады ¹). Бұл жағдайда . (7.3.8)

Айтарлықтай үлкен t кезінде ( < Н кезінде) Ψ_ρ (t) шамасының осцилляциялауды қоятындығына және тең болып шығатындығына назар аударайық.

шамасы жай ғана Ψ_ρ арқылы көрсетіледі:

. (7.3.9)

Бұл нәтиженің физикалық мағынасы уақыт бойынша өзгермейтін конформдық р импульстен Ғалам кеңейген кезде азаятын әдеттегі физикалық импульсіне көшкен кезде анық бола бастайды:

(7.3.10)

Бірінші мүше Минковский дүниесіндегі вакуумдық флуктуациядан әдеттегі үлес (Н = 0 кезінде, (2.1.6), (2.1.7) қар.) болып келеді.

Фазалық ауысулар теориясындағы (3.1.6 қар.) секілді, бұл үлес қайта нормалаумен жойылады. Екінші мүше болса тікелей кеңеюмен тікелей байланысты. Минковский дүниесінде кванттау тұрғысынан алғанда, бұл мүше де Ситтер дүниесінің, Н = 0 кезінде де болатын әдеттегі кванттық флуктуациялармен қатар, (7.3.11) толтыру сандарымен тағы j-бөлшектерді де қамтитындығының есебінен пайда болады.

¹) Барлық физикалық нәтижелердің р ® ∞ кезінде с₁ (р) ® О, с₂ (р) ® -1 болатындай, с₁ (р) және с₂ (р) функцияларының нақты таңдалуына байланысты емес екендігі маңызды.

(7.3.10) көрініп тұрғанындай, j өрісінің ұзын толқынды флуктуацияларының <j ²> шамасына үлесі алшақтайды. <j ²> (7.3.3) шамасының m² ® О кезінде шексіздікке айналуына дәл осы алып келеді.

Шындығына келгенде, алайда, салмақсыз j өрісі үшін <j ²> шамасы тек шексіз ұзақ болатын де Ситтер дүниесінде, бірақ мұның экспоненциалды (немесе квазиэкспоненциалды) кеңеюі әлдебір t = 0 сәтінде (мысалы, Ғаламның тығыздығы планктік тығыздыққа тең болып шыққан кезде) басталатын, күмпеймейтін Ғаламда шексіздікке айналады.

Шынында да, вакуумдық флуктуациялардың (7.3.10) спектрі Минковский дүниесіндегі флуктуация спектрінен тек k 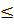кезінде ерекшеленеді. Егер кеңейгенға дейін флуктуацияның спектрі 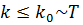кезінде жоғары температуралық әсерлерге [127] орай немесе k 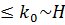кезінде Ғаламның кеңейіп келе жатқан облысының толық бастапқы мөлшерінің О (H^-l) ретке ие болғандығына орай кесілген болса, онда кеңею кезінде спектрдің вакуумдық флуктуациялар толқынының ұзындығының экспоненциалды өсуінің есебінен қайта құрылуы жүреді. Спектр (7.3.10) біртіндеп, бірақ тек k 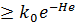импульстары кезінде орнығады. Бұл (7.3.9) интегралда кесілуге алып келеді. Біз үшін одан арғы жерде маңызды болатын, 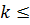Н ұзын толқынды флуктуациялардың үлесімен шектеліп және k_o = 0 (Н) деп шамалап, аламыз:

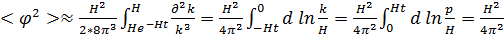t

(7.3.12)

t ® ∞ кезінде <j ²> шамасы (7.3.3) сәйкес, шексіздікке ұмтылады. Осыған ұқсас нәтиже көлемді j скалярлы өрісі үшін де алынады. Бұл жағдайда ұзын толқынды флуктуациялар m² << Н² кезінде өздерін былайша көрсетеді

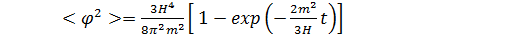(7.3.13)

t 3Н/ m² кезінде <j ²> шамасы, тура салмақсыз өріс (7.3.12) жағдайындағы секілді, сызықтық өседі, ал одан кейін <j ²> өзінің асимптотикалы мәніне (7.3.3) шығады.

Енді алынған нәтижелерге көрнекі физикалық интерпретация беруге тырысамыз. Ең алдымен, <j ²> (7.3.12) шамасына негізгі үлесті экспоненциалды кіші k ( бойынша) бойынша интегралдау беретіндігіне назар аударамыз. Тиісті n_к (7.3.11) толтыру сандары экспоненциалды үлкен болып шығады. Үлкен кезінде салмақсыз өріс үшін <j (х) j (у)> корреляциялық функциясы [203] тең:

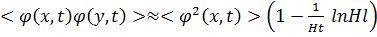(7.3.14)

Бұл әртүрлі нүктелердегі j (х) және j (у) өрістерінің мәндерінің экспоненциалды үлкен l 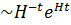қашықтықтарға дейін жақсы корреляцияланғандығын білдіреді. Осы критерийлердің барлығы бойынша k << Н^-1 болатын j өрісінің ұзын толқынды кванттық флуктуациялары әлсіз біртексіз (квази)классикалық j өрісінің инфляциялық сатысында генерацияланатын ретінде көрініс табады (бұл сұрақты § 2.1 талқылауды қар.).

Осыған ұқсас нәтижелер көлемді m² << Н² өрісі үшін де әділ. Бұл жағдайда <j₂> негізгі үлесті k 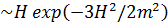болатын модтар береді, ал корреляцияның ұзындығы Н^-1 ехр (3 Н²/2 m² ) ретке ие, 32 сур. қар.

Бұл жерде маңызды түсіндірме бере кету керек. Кеңейіп келе жатқан Ғаламда бөлшектердің пайда болу теориясын құраған кезде мамандар нақты бөлшектерді вакуумдық ауытқулардан бөліп алудың салыстырмалылықтың жалпы теориясында бірмәнді емес болып табылатындығымен ұшырасты. Біз осыған ұқсас жағдайдың мысалымен ұшырастық та.

32 сур. Кеңейген кезде туындайтын квазиклассикалық j өрісінің бөлінуі. Салмақсыз өріс үшін дисперсия D (Н/2p) V Ht тең, ал корреляцияның сипатты l ұзындығы Н^-l ехр (Ht) тең. m << Н болатын көлемді өріс үшін уақыттан кейін және болатын тепе-тең бөліну орнығады.

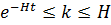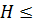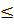Атап айтқанда, (7.2.3) координаталар жүйесінде кванттау кезінде H болатын, қарастырылып отырған ұзын толқынды флуктуациялар p H 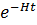импульстарына жауап береді. р-кеңістікте тиісті толтыру сандары мүлдем уақытпен экспоненциалды өспейді.

Үлкен ǀ х - у ǀ кезінде j (х) және j (у) арасындағы корреляция шамалы. Осылайша, де Ситтер дүниесінде (7.2.3) кванттау тұрғысынан алғанда, біз кванттық флуктуациялармен істес болып отырмыз. Алайда, k=p 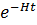физикалық импульстар кезінде және үлкен l 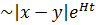физикалық қашықтықтардағы корреляция кезінде толтыру сандары тұрғысынан алғанда, біз квазиклассикалық әлсіз біртексіз j өрісімен істес болып отырмыз.

Талқыланып отырған айырма Ψ_ρ (t) (7.3.8) функциясын және осының квадраты физикалық k импульстың терминдеріндегі спектрді (7.3.10) беретін Ψ" (t) = ' Ψ_ρ е^(3/2)Нt функциясын салыстырудың мысалында жақсы көрінеді:

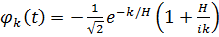(7.3.15)

k >> Н кезінде біз тұрақты амплитудамен осцилляциялайтын өріспен істес боламыз. Алайда уақыт өте келе, k = шамасы Н азырақ болып шыққан кезде, осцилляциялар тоқтап, бөліну фазасы бойынша қатып қалған Ψk (t) өрісінің амплитудасы экспоненциалды арта бастайды:

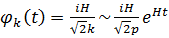(7.3.16)

толтырылу сандарының экспоненциалды өсуіне дәл осы әкеледі.

Бұл құбылыс бізге бозеконденсация және өріс теориясында симметрияның бұзылуы туралы мәселені талқылаған кезде кездескен де болатын. Классикалық хиггстік өріс түзіле отырып, орнықсыздық дәл осылай дамиды, (1.1.6) формуланы қар. Айырма Минковский дүниесінде симметрия бұзылған кезде нөлдік k импульсы бар моданың бәрінен жылдамырақ өсетіндігінен тұрады. Кеңейіп келе жатқан Ғаламда k импульсы модалардың кез келгенінде жылдам кемиді. Бұл әртүрлі k импульстары бар модалардың бірдей дерлік өсуіне алып келеді, j өрісінің біртексіздігі тек экспоненциалды үлкен ауқымдарында ғана елеулі болғанымен, осының нәтижесінде классикалық j өрісі біртексіз бола бастайды, (7.3.14) қар.

Зерделеніп отырған құбылыс пен Минковский дүниесінде симметрияның тосыннан бұзылуы арасындағы тағы бір маңызды айырмашылық де Ситтер дүниесінде классикалық j өрісінің генерациясының мәжбүрлі түрде жүретіндігінен тұрады. j өрісінің ұзын толқынды ұйытқуларының өсуі тіптен бұл энергетикалық тиімсіз болған кезде, мысалы, m² > О кезінде де (тек m² < Н² шарты кезінде ғана) жүреді.

Кеңейген кезде классикалық скалярлы j (х) өрісінің қарастырылып отырған генерация процесін, бұл өрістің кванттық флуктуацияларының квазиклассикалық j (х) өрісіне ауысуының есебінен броундық қозғалыстың нәтижесі ретінде түсіндіріп беруге болады. р = const болатын әрбір осы мода үшін бұл ауысу тиісті физикалық k = импульсы Н – пен теңескен кезде жүреді. Бұл кезде Ψ_ρ (t) толқынының амплитудасы «қатады», (7.3.8) қар. e^ipx фазасының үйлесімсіздігіне орай, әртүрлі импульстары бар толқындар классикалық j (х) өрісінің шамасына әртүрлі белгідегі үлестерін енгізеді, бұл

кеңейген кезде пайда болатын өрістің кездейсоқ бөліну дисперсиясының квадратын сипаттайтын (7.3.9) формулада көрінісін табады. Броундық бөлшектің диффузиясының жылдамдығы туралы стандартты есептегі секілді, оның бастапқы нүктеден қашықтауының орташа квадраты процестің жүру уақытына тура пропорционал болып шығады ((7.3.12) қар.).

j өрісінің әрбір белгіленген нүктедегі диффузиясын Р_с (j, t) ықтималдықтың бөлінуінің көмегімен сипаттаған, осы j өрісін t уақыт сәтінде осы нүктеде табу ыңғайлы. Бұл жерде с жұлдызшасы осы бөлінудің, түсіну қиын болмайтындай, бір мезгілде t уақыт сәтінде осы j өрісімен толтырылған бастапқы d³x (7.2.3) координаталық көлемнің үлесінің мағынасына ие болу айғағын көрсету үшін қызмет етеді. Кеңейіп келе жатқан Ғаламда салмақсыз j өрісінің Рс (j) бөліну эволюциясын диффузия теңдеуін шеше отырып табуға болады [204, 134, 135]

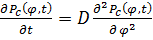(7.3.17)

D диффузия коэффициентін табу үшін, (7.3.17) – де

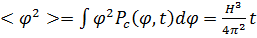екендігін ескереміз.

Бұл ара қатынасты t бойынша дифференциалдай және (7.3.17) пайдалана отырып, D= 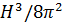аламыз.

Бастапқы 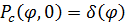шарты бар (7.3.17) теңдеудің шешімі 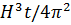(7.3.12) дисперсиямен 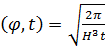exp 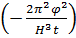гаусстық бөлінумен берілетіндігіне көз жеткізу қиын емес (7.3.12).

ǀ m² ǀ << Н² салмақтың классикалық скалярлы өрісінің генерациясын қарастырған кезде k > Н импульстармен кванттық флуктуацияларды k < Н облысына айдау жылдамдығымен байланысты D диффузия коэффициенті бұрынғыдай болып қалады, өйткені k 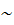Н болатын модтардан (j₂) үлес ǀ m² ǀ ~ Н² кезінде m тәуелді емес. Дәл осы себеппен (j₂) (7.3.13) шамасы салмақсыз (7.3.12) өріс жағдайындағыдай өседі. Алайда кейіннен, процестің бірінші сатыларында пайда болған ұзын толқынды классикалық j өрісі қозғалыстың классикалық теңдеуіне сәйкес j = 0 нүктесіне баяу домалаудың есебінен азая бастайды:

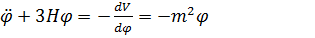(7.3.19)

Бұл ақыр соңында оның (7.3.13) шекті мәнінде <j₂> шамасының тұрақтануына алып келеді де. Бұл процесті сипаттау үшін диффузия теңдеуін біршама ортағырақ түрде жазу керек [205]

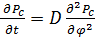+b (7.3.20)

мұнда, бұрынғыдай, D = ; b - j = теңдеуінен анықталатын қозғалғыштық коэффициенті. (7.3.19) көмегімен баяу өзгеретін j (ф << 3Н ф) өрісі үшін мынаны аламыз:

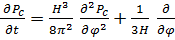
(7.3.21)

(7.3.21) теңдеуді алғаш рет А. Старобинский алған болатын [134]. Бұл теңдеудің толығырақ шығарылуын [186, 135, 132, 206] жұмыстардан табуға болады. Оны V (j) = mj₂/2 + V (О) жағдайы үшін шешу шынында да Рс (j, t) (7.3.13) формуламен анықталатын дисперсиямен бөлінуіне алып келеді. V (j) потенциалдарының ортағырақ санаты үшін әділ болатын шешімдер келесі параграфта, кеңейіп келе жатқан Ғаламда туннельдендіру мәселесімен байланысты талқыланатын болады.

(7.3.21) теңдеуді шығарған кезде Н шамасының j өрісіне тәуелді емес екендігі есте ұсталған болатын. Ортағырақ жағдайда (7.3.21) теңдеуі былайша жазылады:

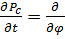
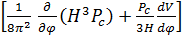(7.3.22)

Қатаң айтқанда, (7.3.22) теңдеуі әзірге өрістің біртексіздіктерінің метрикаға кері әсері тым үлкен болмай тұрғанда, тек j өрісінің айтарлықтай шағын вариациялары кезінде де әділ.

Солай болса да, бұл теңдеудің көмегімен Ғаламның жаһандық құрылымы туралы маңызды ақпарат алуға болады (10 тар. қар.).