Басты геодезиялыҚ есептерді эллипсойд бетінде есептеу

СССР кезіндегі АГТ I класты триангуляция звеноларын теңестіру кезінде есептеудің екі тәсілі кеңінен қолданылады, олар: бастапқы пункттың белгілі геодезиялық координаттары бойынша; өлшенген сфералық қашықтық пен осы бағыттың геодезиялық азимутымен екінші пункттың геодезиялық координаттарын табу керек; годезиялық сызықтың ұштарының белгілі геодезиялық координаттары бойынша геодезиялық сызықтың ұзынды мен тура және кері геодезиялық сызық азимутын есептеу қажет. Бірінші есептеу – тура геодезиялық есепп деп аталады, ал екіншісі – кері геодезиялық есеп деп атады. Көп жағдайда тура және кері геодезиялық есептеулерді басты геодезиялық есептер деп атайды.

Төменде көрсетілген жұмыстар геозиялық координаттар функциясының басты геодезиялық есептерін шешу үшін арналған.

3.1. Басты геодезиялық есептерді есептеудің жолдары мен әдістері

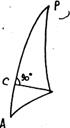
Жалпы жағдайда басты геодезиялық есептерді шеушу жолдары РАВ полярлы үшбұрыш элементтерін есептеу мен тең келеді. Мұндағы Р – эллипсоидтың полюсі, А және В – геодезиялық пункттер. Сфералық үшбұрышты РАВ есептеу үшін оның кез келген үш элементі белгілі болу қажет. Тура геодезиялық есептерді есептеу кезінде белгілі элементтер ретінде қолданылатындар:

РА = 90 - В_В, AB =S _АВ ·

сфералық /_ РАВ = А_AB – геодезиялық сызықтың АВ тура азимуты.

Міндетті түрде анықтау керек:

РВ=90-В_B и ∟РВА=A_BA – геодезиялық сызықтың АВ кері азимуты,

∟APB=L_B-L_A – пункттер бойлығының айырмашалығы.

Кері геодезиялық есептерді есептеу кезінде белгілі элементтері ретінде: АР = 90-В_A, ВР - 90-B_β және сфералық ∟АРВ = L_A – L_B екі пункттың бойлықтарының айырмашылығы. Міндетті түрде пункттер арасындағы қашықтықты есептеу керек: АВ = S_AB, ∟РАВ = А_AB геодезиялық сызықтың тура азимуты АВ және 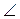РВА=Α_ВА – геодезиялық сызықтың AВ кері азимуты.

Полярлы РАВ үшбұрышынэлементарлы функциялар көмегімен есептеу мүмкіндігі тек осы үшбұрыш тұрақты радиустың сферасында орналасқан болса орындалады, демек үшбұрыш шарда орналасқан болса. Себебі референц-эллипсоид бетіндегі қисықтың радиусы өз орнының ендігі мен азимут бағытына байланысты өзгерсе, онда сфералық үшбұрыштың РАВ элементарлық функциялар көмегімен есептеулері мүмкін болмайды. РАВ сфералық үшбұрышын есептеу кезінде элементарлы функцияларды қолдану арқылы үшбұрыштың берілген дәлдігімен жоғарыда аталған тәсілдердің бірін қолданып есептеуге болады. Сондықтан, кез келген геодезиялық есептерді шешу кезінде әдістемелік қателіктер жіберілетінін естен шығармауымыз қажет, бір үшбұрышты әртүрлі тәсілмермен есептейтін болсақ, әр тәсіл бойынша есептеу әдісіне байланысты өсімшесінің қателігін анықтайтын мәндер шығады.

Сфералық үшбұрыштың РАВ өлшемдеріне байланысты бірнеше тәсілдермен есептелуі мүмкін. Сондықтан барлық үшбұрыштарды АВ қабырғаларына байланысты шартты түрде 4 топқа бөлуге болады.

I. кішкентай, егер S≤ 45 км.

2. орташа, егер S ≤ 600 км.

3. үлкен, егер S ≤ 5000 км

4. өте үлкен, егер S≤ 19000 км

Қабырғасы АВ 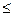600 км болатын үшбұрышты есептеу кезінде кіші көмекші АВС үшбұрышын есептеу геодезиялық координаттарының айырмашылығы арқылы жеңілдетілген формулалармен есептеуге болады. Осындай есептеу жолдары жанама есептеу жолдары деп аталады.

Қабырғалары АВ > 600 км болатын үшбұрышты тура есептеу жолдарымен орындайды, демек міндетті түрде тікелей полярлы үшбұрыштың ендігі, бойлығы және азимуты есептеледі.

Басты геодезилық есептерді тура жолмен есептеу кезінде көмекші сфераның негізгі есептеу тәсілдері қолданылады. Бұл жағдайда басты геодезиялық есептеулер реті келесідей болады:

:

I. Эллипсоидтан шарға аусу заңдылығына байланысты сфералық үшбұрыш РАВ элементтерінің көмекші полярлы үшбұрыш ΡΆ'B’ элементтеріне ауысуы;

2. Сфералық үшбұрыш Р'А'В' тұйықталған формулалармен есептеу, яғни ендігін, бойлығын және азимутын анықтау;

3. Сфералық үшбұрыш ΡΆ'Β элементтерінің сфероидалдық үшбұрыш РАВ элементтеріне аусуы да тура аусу заңдылығына байланысты өзгеруі;

Эллипсоид бетіндегі үшбұрыштарды есептеу тәсілдерінің айырмашылығы көмекші сфераны таңдауда және эллипсоидтан шарға аусу және кері заңдылығы ретінде бекітіліп орындалады.

Сфероидалдық үшбұрыштарды жанама әдіспен есептеу кезінде геодезиялық координаттар функциясының әркелкі реттілігімен S және е² дәрежелерімен анықталады. Жалпы жағдайда сфероидалық үшбұрыштарды есептеу формуласы төмендегідей болады:

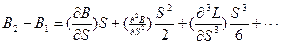
(1)

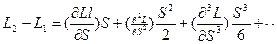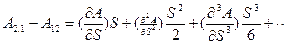Әлбетте, геодезиялық есептеулерді орындау үшін (1) теңдеуінде көрсетілген жеке туындыларды анықтау қажет, себебі геодезиялық координаттар айырмашылығының қажетті дәлдігін есептеу керек.

Басты геодезиялық есептедің барлық есептеу тәсілдерінің (1) теңдеуіндегі жеке туындыларды есептеуіне негізделіп, жіктеу сандарының кішейтілуіне немесе есептеу коэфициенттерінің қатарға жіктелуіне байланысты тек әдістері бойынша ажыратылады.

Көмекші С нүктесінің бұрышы 90° құрайтын тәсіл қатар бойынша жіктелі коэфициентінің өсімшесін кішірейту үшін қолданылады.

Орташа аргументтерді енгізі арқылы орындалатын орташа аргументтер тәсілі, яғни орташа ендік, бойлық және азимут (1) теңдеуінен жұп қатардағы сәйкестік қатарын ұлғайтатын жеке туындыларын шегеріп тастауға мүмкіндік береді.

Геодезиялық практикадағы қашықтығы 600 км дейінгі геодезиялық есептерді шешу кезінде көп қолданылатын қосымша нукте тәсілі болып саналады. Қосымша нүкте тәсілі бойынша есептеу реттілігі:

I) АВС үшбұрышын Лежандр тәсілімен АС және ВС доғаларын есептеу және С нүктесінің координаттарын анықтау:

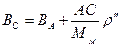L_C=L_{A (2)}

Байқайтын болса С нүктесінің ендігі В нүктесінің ендігімен сәйкес келеді, демек РСB = 90° бұрышы РВC бұрышына біршама тең боламайды.

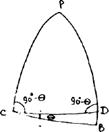2) СBD үшбұрышын есептеу кезінде D нүктесі РCD және РDС бұрыштары тең болған жағдайда PB меридианында болады. Үшбұрыштың есептерінен С және Д (В) нүктелерінің бойлықтарының айырмашылығы мен Д (С) және В нүктелерінің ендігінің айырмашылығы анықталады.

3) Сфероидалдық үшбұрыштың СРD есептеуінен PC және РВ меридиандарының жақындауын анықтау.

4) А_BA кері азимутының В нүктесінің ендігі мен бойлығын анықтау.

Арақашықтығы 600 км дейінгі кері геодезиялық есептерді шешу үшін орташа аргументтер формулаларын қолдану керек. Сол себепті есептеу реттілігі төмендегідей болады:

1) Орташа аргументтерді анықтау:

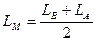
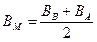(3)

2) (I) теңдеуін орташа аргументін анықтап, геодезиялық сызықтың орташа аргументін А_M пункттер арасындағы қашықтығы S_AВ арқылы есептеу.

3) АВ сызығының ортасында орналасқан нүктелер координаттарынан B_m, L_m орташа координаттар түзетулерімен есептеп РА және РВ меридиандарының жақындауын есептеу.

4)Соңғы A_AB және А_BА азимуттарын және Sab қабырғаларының ұзындығын анықтау.

№ 3 Референц-эллипсоид бетіндегі геодезиялық есептерді шешу.

1. АВС үшбұрышындағы сфералық бұрышы А тең, геодезиялық сызықтың тура азимуты мен А нүктесінің координаттары, қабырғаларының АВ ұзындығы белгілі А және В пункттерінің арасындағы тура геодезиялық есептерді шешу. Бастапқы міндерін №2 тапсырмадан алу керек.

А пунктінің бойлығы L_А =64º12'36.363'' тең, есептеу кезінде көмекші нүктелердің формулаларына жетекшілік ету керек.

2. Бұрынырақ есептелген А және В пункттерінің координаттарының мәндерін қолдана отырып, кері геодезиялық есепті шешу керек: демек АВ қабырғасының ұзыдығын анықтау қажет, орташа аргументтер формулаларына сәйкес А_АВ және A_ВА тура және кері азимуттарын есептеу.

Тамсырма № 3 көмекші нүкте тәсілінің нәтижелерімен тура геодезиялық есепті шешу үшін А нүктесінің геодезиялық координаттарын № 1 және № 2 тапсырмаларда алынған нәтижесі бойынша, № 2 тапсырмадан алынатын АВ арақашықтығын және сфералық бұрышы А тең болатын АВ тура азимут сызығын анықтау.

Тура геодезиялық есептерді шешу кезінде алынған А және В пункттерінің бастапқы ендігі мен бойлығы белгілі болса, кері геодезиялық есепті шешу үшін орташа аргументтер фоомуласы қолданылады. Есептеу нәтижелері: тура геодезиялық есепті шешу кезінде алынған нәтиже АВ қабырғасы мен А_АВ және В_ВА азимуттарына тең болуы қажет.

ҮЛГІ

Тапсырманы есептеу және өңдеу (нөлдік нұсқа)

Бастапқы мәндері:

В_А = 53°5Ч'30,000" е ^{г =} 0,0067385254

L_A = 64°12'36,363" ρ’'= 206264,81"

S_AB= 131615,32 м sin A_AB 0,66013379

A_AB=41º18’36.280’’ cos Aab = 0.75114803

N_A= 6392229,5 м m_a = 6377316.4

I. Көмекші нүктелер тәсілімен есептелетін тура геодезиялық есептерді шешу.

№	Формулалар	Нәтижелері
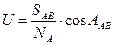		0.01546605
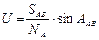		0.01359208
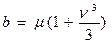		010.01546695 53’10.287
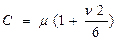		0.01359154
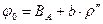		54º47'40,287”
	Tgφ0	1.41730778
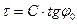		0.01922633
	Cosφ0	0.57651041
	Λ=c/cosφ	0.0235755
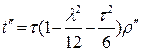		1º06’12.907’’
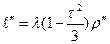		1º21’02,177”
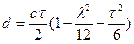		0.0001309
	∆φ=b-d	0.0153360
	V12=1+e2cos2B	1.0023383
	∆B=V12∆φ(1-3|4 e2sin2B∆φ-e2\2 cos2B∆φ2)ρ’’	0º52’50.428’’ 0.0153718
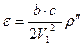		21.617’’
	BB=BA+∆B	54º47’20.428’’
	LB=LA=ℓ’’	65º33’38.540’’
	A2.1=A1.2+180º+t’’-ε’’	222º24’27,570’’

2. Орташа аргументтер формуласымен орындалатын кері геодезиялық есептерді шешу.

α₁ = 103422,05 cos B_m

α₂= 9,5144cosB_m + . 0,5525соs ³ B_M - 0,0078cos^sB_m.

α₃= -ΙΟ, 1287 cos В_m +· ΙΟ, 1287 cos³B_m

α₄=103422,05-696,9116cos²B_m+4,6954cos⁴B_m-0,0310cos⁶B_m

α₅=30,3860+10,3334cos²B_m-0,2061cos⁴B_m+0,0014cos⁶B_m

α₆=0,2048+0,4192cos²B_m-0,0124cos⁴B_m^’

α₈=2,9381+0,0132cos²B_m

α₉=1,9587cos²B_m+0,0132cos⁴B_m^’

Формулалар	Нәтижелер	Формулалар	Нәтижелер
B1	53º54’30,000’’	Cos4Bm	0,1154066
B2	54º47’20,428	Cos5Bm	0,06726
∆B	0º52’50,428’’	Cos6BM	0,0392
∆B’’	+3170,428	sinBm	0,8125789
Bm	54º20’55,214’’	Α1	60279,665
L1	64º12’36,363’’	A2	5,654
L2	65º33’38,54	A3	-3,898
ℓ=L2-L1	1º21’02,177’’	Α4	103185,84
ℓ’’	4862,177’’	A5	-26,899
∆B=∆B/10000	0,3170428	A6	-0,064
ℓ=ℓ/10000	0,4862177	A7
∆B2	0,1005161	A8	2,949
e2	0,2364076	a9	0,667
∆B2ℓ	0,0488727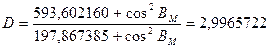
∆B ℓ2	0,0749513
∆B3	0,318679	A1ℓ	29309,040
ℓ3	0,1149455	A2∆B2ℓ	0,276
Cos2Bm	0,3397155	A3 ℓ	-0,448
Cos3Bm	0.1980036	Σ1	29308,868

A4∆B	32714,327	S sinAm=DΣ1	87826,139
A5∆B ℓ2	-2,016	S cosAm=DΣ2	98024,396
A6εB3	-0,009	tgAm=DΣ1/DΣ2	0,8959582
Σ2	32712,309	Am	41º51’32,404’
A7 ℓ	4862,177	sinAm	0,6672999
A8∆B2ℓ	0,144	cosAm	0,7447891
A9ℓ3	0,077	S’=DΣ1/sinAm	131614,19
Σ3	4862,398	CcP     ∆A	13614,18     3951,082’’
A1.2=Am-∆A/2	41º18’36,899’’
A1.2=Am+180+-∆A/2	222º24’27,981’’