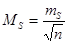Арифметична середина та її властивості.

Рывень2

48. Карта – зменшене, спотворене під впливом кривини Землі зображення на площині горизонтальної проекції значної частини або всієї земної поверхні, побудоване за певними математичними законами в умовних знаках. При складанні карт перш за все будують географічну сітку меридіанів та паралелей, яку називають картографічною сіткою.

Планом називається зображення порівняно невеликих ділянок місцевості, побудоване на площині в умовних знаках в ортогональній проекції без врахування кривини Землі. Під час побудови планів точки місцевості проектують на площину прямовисними лініями. Таке проектування називається ортогональним.

49. Масштаб - це відношення довжини відрізка на плані чи карті до його горизонтальної проекції на місцевості.

Словесний масштаб – це запис масштабу на карті словами. Наприклад, запис на карті «в 1 сантиметрі 100 метрів» означає, що масштаб карти 1:10 000 .

Користування числовим масштабом потребує обчислень. Тому частіше використовують графічні побудови, так звані, лінійні та поперечні масштаби.

Лінійний масштаб – це графічне зображення числового масштабу. Для побудови лінійного масштабу на відрізку прямої відкладають (в сантиметрах) декілька відрізків однакової довжини, які називаються основою масштабу. Масштаб з основою 2 см називається нормальним. Ліву основу поділяють на 10 рівних частин.

Поперечний масштаб застосовують для визначення довжин ліній на карті з точністю десятих часток міліметра. Для його побудови на відрізку прямої АВ відкладають декілька основ масштабу. Якщо основа 2 см, то такий масштаб називається нормальним

50. Масштаб - це відношення довжини відрізка на плані чи карті до його горизонтальної проекції на місцевості.

графічна точність масштабу – це горизонтальна віддаль на місцевості, яка на карті (плані) даного масштабу дорівнює 0,1мм. Отже, необхідно визначити, якій горизонтальній проекції на місцевості відповідає відрізок 0,1мм на карті:

51. Умовні знаки – графічні рисунки відповідних розміру, форми і кольору, якими відображаються на картах об’єкти місцевості. Їх прийнято поділяти на масштабні(ліси,луги), напівмаштабні або лінійні(ЛЕП,дороги), позамасштабні(колодязі,окреме дерево) та допоміжні (пояснювальні-характеристика доріг,річок).

52. Масштабними називаються умовні знаки, якими відображають предмети місцевості з дотриманням їх розмірів(ліси,луки,озера сади).

53. Лінійніоб’єкти зображають на планах і картах напівмасштабними умовними знаками, тобто лише їх довжина виражається в масштабі плану чи карти(дороги,ЛЕП,лінії зв’язку).

54.Предмети місцевості, які не можуть бути виражені в масштабі плану чи карти внаслідок своїх малих розмірів зображають позамасштабними умовними знаками(Колодязі,окреме дерево,пам’ятники).

55.Всі написи, пояснення відносяться до допоміжних умовних знаків(характеристика лісу,річок,озер,доріг).

56. Орінтування ліній- це визначення напряму даної лінії відносно іншого напряму прийнятого за вихідний.

Дирекційним кутом a називають горизонтальний кут, який відраховують від північного напряму осьового меридіана або лінії, що паралельна до нього, за годинниковою стрілкою до заданої лінії (в межах від 0 до 360 ).

57. Істинним азимутом 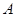називається горизонтальний кут, який відраховується від північного напряму істинного меридіана або лінії, що паралельна до нього, за годинниковою стрілкою до заданої лінії (в межах від 0 до 360 ).

зближення меридіанів 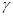- кут між істинним меридіаном і лінією сітки.

Якщо точка знаходиться на схід від осьового меридіана, то значення 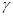матиме додатній знак, якщо на захід – від‘ємний.

58. Магнітним азимутом 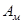називається кут, який відлічується від північного напряму магнітного меридіана або лінії, що паралельна до нього, за годинниковою стрілкою до заданої лінії (в межах від 0 до 360 ).

схилення магнітної стрілки 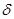- кут між магнітним та істинним меридіанами.

59. Румбом називається горизонтальнийгострий кут, що відлічують від найближчого напрямку меридіана (північного або південного) або ліній паралельній йому до напрямку на дану точку.

60. На аркушах карти лінії, що паралельні до осьового меридіана, є вертикальні кілометрові лінії. Тому, для вимірювання дирекційного кута через початкову точку А (лінії АВ) проводять пряму, що паралельна найближчій вертикальній кілометровій лінії і від її північного напряму транспортиром вимірюють дирекційний кут лінії АВ.

61. Для визначення істинного та магнітного азимутів необхідно використати графік, який розміщений під південною рамкою карти з лівої сторони від числового масштабу Величини 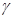і 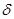виписують з карти, враховуючи їх знаки.

Істинний та магнітний азимути обчислюють за формулами

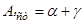. (3.1)

.

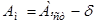65. Меридіа́н, полуденник (лат. meridies — полудень) — уявна лінія перерізу поверхні земної кулі площиною, проведеною через будь-яку точку земної поверхні і вісь обертання Землі. Кожен меридіан перетинається з усіма іншими в двох точках: напівнічному і південному полюсі.

Паралель географічна (рос. параллель географическая, англ. geographic parallel, нім. geographische Parallele f, Breite f, Breitenkreis m) – лінія перетину поверхні земної кулі площиною, паралельною до площини екватора. Екватор - найдовша паралель.

66. Геодезична широтаВ – це гострий кут, утворений нормаллю до поверхні еліпсоїда і площини екватора. Геодезичні широти відлічують від площини екватора в межах 0º - ± 90º. Для точок північної півсфери вони додатні, для південної - від’ємні.

Геодезична довгота L - це двогранний кут, утворений площиною початкового меридіана і площиною меридіана, що проходить через задану точку. Геодезичні довготи, відлічувані від площини початкового меридіана на схід в межах 0º - + 180º, називають східними, а на захід – західними.

67. Для однозначності приймають, що в кожній зоні ордината осьового меридіана кожної зони дорівнює 500 км, тобто значенню ординати точки O (див. рис. І.2.13) Y0 = 500 км. Тоді точки, розташовані на захід і на схід від осьового меридіана, матимуть додатні значення ординат.

68. Загальноземний еліпсоїд – це еліпсоїд обертання, зорієнтований у тілі Землі так, що його центр збігається з центром мас Землі, площина його екватора – з площиною екватора Землі, і сума квадратів відхилень від поверхні геоїда є мінімальною.

69. Референц-еліпсоїд – це еліпсоїд, що найкраще описує фігуру Землі для певної території (країни). У різних країнах вчені на основі градусних вимірювань отримали різні розміри референц-еліпсоїдів, які подано у неповній таблиці таких визначень

70. Рельєф – це сукупність нерівностей земної поверхні, що утворюються на межі літосфери з атмосферою і гідросферою. Є такі основні форми рельєфу: гора, улоговина, хребет, лощина, сідловина.

71. Способи зображення рельєфу:

· Світло-тіньове зображення рельєфу (випуклі форми рельєфу більш освітлені, впадини – затемнені);

· За допомогою штрихів (рельєф зображають виходячи з принципу прямовисного освітлення земної поверхні, при якому вона буде менш освітленою, коли крутизна схилу буде більша. Відповідно до крутизни схилу будуються шкали, де вказано співвідношення товщини штриха до відстані між штрихами. Використовувався цей метод в 18-19 ст.);

· Гіпсометричний (кожному діапазону висот відповідає певний колір або його відтінок);

· За допомогою горизонталей (основний).

72. Абсолютна висота точки місцевості назив. відрізок прямовисної лінії від точки на фізичній поверхні до рівневої поверхні.

Перевищення – різниця висот двох точок.

73. якщо за рівневу поверхню приймають будь яку іншу, а не вихідну поверхню то висоти точок визначені відносно такої поверхні називають умовним.

74. Горизонталі – це лінії, які з’єднують точки з однаковими висотами. Вони мають наступні властивості.

· Горизонталі – зімкнуті криві в межах плану або карти.

· Горизонталі на карті або плані є неперервними лініями. Вони можуть перериватись лише через яри і ріки.

· Горизонталі не можуть пересікатись і розгалужуватись. Винятком може бути тільки нависна скеля.

· Віддаль між горизонталями характеризує крутизну схилу, тобто чим ближче розташовані горизонталі на карті, тим крутіший схил. Напрямок схилу позначається схилштрихами (бергштрихами).

Горизонталі мають висоти, кратні висоті перерізу рельєфу

75. Номенклатура – це умовне літеро-цифрове позначення аркушів карт та планів, яке дозволяє визначити положення на земній кулі тієї частини території, що зображена на тих листах.

76. Середня квадратична похибка - це міра розсіювання результатів вимірювань навколо істинного значення вимірюваної величини. Вона є основним критерієм оцінки точності геодезичних вимірів.

Якщо виміри рівноточні і відоме істинне значення вимірюваної величини то СКП обчислюється за формулою Гауса. ,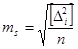

77. Середня квадратична похибка - це міра розсіювання результатів вимірювань навколо істинного значення вимірюваної величини. Вона є основним критерієм оцінки точності геодезичних вимірів

Якщо виміри рівно точні і за найбільш імовірне значення виміряної величини приймають середнє арифметичне то СКП одного виміра обчислюється за формулою Бесселя

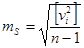
Рівень3

78. Геодезія – прикладна математична наука, що вивчає методи визначення форми та розмірів планети Землі її гравітаційного поля, зміни цих параметрів у просторі та часі, розробляє методи зображення поверхні землі на картах і планах, способи вимірювання на місцевості а також розробляє методи розв’язування наукових та інженерних задач.

З грецької мови слово “геодезія” перекладається як “землерозділення”. Проте точніше дає змогу відтворити суть геодезичної науки слово “земле вимірювання”.

Під дійсною поверхнею Землі розуміють її фізичну поверхню, на якій виконуються наземні вимірювання, тобто поверхню суші і незбурену поверхню морів, океанів та озер.

У завдання вищої геодезії не входить безперервне визначення фізичної поверхні Землі, наприклад, у вигляді карт. Цим займаються інші розділи геодезії – топографія, аерознімання. Основне завдання вищої геодезії формулюють як визначення положення деякої мережі опорних точок у єдиній системі координат. На основі цієї мережі і вивчаються форми й розміри планети Земля, її гравітаційне поле, а за зміною координат пунктів цієї мережі вивчається зміна названих параметрів у просторі та часі. Саме ці питання вивчає частина геодезії, яку називають вищою геодезією.

Наведене тут ширше визначення предмета геодезії (не вищої геодезії) охоплює ще і методи топографічного знімання, які вивчає наука “геодезія”. І це небезпідставно, оскільки “топографія” є частиною “геодезії”.

Отже, доходимо висновку, що геодезія складається з двох основних частин: вищої геодезії та топографії. Вища геодезія вивчає уявну поверхню, так звану рівневу поверхню сили ваги Землі, а топографія вивчає частинами дійсну поверхню Землі. Дуже важливу роль у геодезії відіграє поверхня геоїда, тобто рівнева поверхня поля сили тяжіння (сили ваги), що проходить через початок відліку висот. Ця поверхня близька до незбуреного середнього рівня океанів і з’єднаних із ними морів. Тому часто на це вказують, навіть даючи визначення геоїда. Через різницю температур і солоності води в різних частинах Світового океану і з деяких інших причин поверхня геоїда строго не збігається зі вказаною рівневою поверхнею. За деякими оцінками, такі відхилення можуть сягати 1 м. Ця обставина змушує розрізняти поверхню геоїда і так звану топографічну поверхню океанів та морів.

Зауважимо ще, що геодезія може бути розділена не на дві, а на декілька наукових дисциплін:

1. Вища геодезія. 2. Топографія. 3. Аерофотогеодезія і фотограмметрія.4. Прикладна (інженерна) геодезія. 5. Геодезична гравіметрія. 6. Геодезична астрономія. 7. Космічна геодезія. 8. Картографія. 9. Геодезичне приладобудування. 10. Економіка й організація геодезичних робіт.

Геодезія спирається, передусім, на математичні дисципліни. Крім того, для вивчення геодезії важливо знати фізику, особливо оптику і фізику атмосфери, геофізику, геоморфологію. Геодезія тісно пов’язана з астрономією. Геодезія необхідна геології, геофізиці, приладознавству, геоботаніці, інженерним наукам. Будівництво залізниць, шосе, каналів, метро вимагають знання геодезії. Геодезія дуже потрібна військовій та морській справі.

79. Історичний аспект розвитку геодезії й уявлень людства про форму й розміри Землі висвітлено в топографії. Тут ми тільки вкажемо, що в розвитку геодезії можна виділити найважливіші етапи. Перший етап, коли давні індуси, вавілоняни й греки до Піфагора (VI ст. до н. е.) вважали Землю плоскою, або плоско-опуклою, і такою, що тримається на підпірках. Піфагор (580–500 рр. до н. е.) припустив, що Земля, як “найдосконаліше тіло”, має форму кулі. Великий грецький учений Арістотель (384–322 рр. до н. е.) довів кулеподібність Землі за формою тіні на диску Місяця під час місячних затемнень. . Є відомості, що ще до Арістотеля були спроби визначити розміри земної кулі. Обґрунтував розміри Землі як кулі Ератосфен (276–196 рр. до н. е.).

З цього періоду і до кінця XVII віку – другий етап. Землю вважали кулею. У 829 р. арабські вчені визначили розміри Землі. Результат цього визначення виявився близьким до сучасних даних: для дуги в 1° за меридіаном араби отримали 111,8 км. З епохи великих геофізичних відкриттів починається період нового природознавства. Від цього періоду бере початок і нова геодезична наука. Представники: , Снелліул , Пікар , Ньютон.

Третій етап – кінець XVII і до середини XIX століття, коли Землю вважали приплюснутою кулею, тобто сфероїдом (сфероїдальність Землі доведена Ньютоном).

Четвертий етап, коли наука дійшла висновку, що сфероїд – тільки друге наближення до істинної фігури Землі. Цій істинній фігурі у 1873 році німецький фізик І.В. Лістінг дав спеціальну назву – геоїд.

П’ятий – сучасний етап. Детально вивчається геоїд, квазігеоїд, у різних країнах визначаються відхилення геоїда від деяких еліпсоїдів із певними розмірами і у певний спосіб орієнтованими в тілі Землі.

Сьогодні супутникові технології, які є могутнішими засобами, ніж наземна геодезія, для вивчення форми та розмірів Землі, її гравітаційного поля, тобто поля сили ваги. Технології космічної (супутникової) геодезії дають також змогу визначати взаємне положення точок земної поверхні, будувати просторові опорні геодезичні мережі і виконувати топографічне знімання з метою складання планів та карт.

80. Відправною точкою становлення самостійної геодезично-картографічної

служби України стала постанова Кабінету Міністрів України № 306 від 1 листопада 1991 р. “Про створення Головного управління геодезії, картографії та кадастру при Кабінеті Міністрів України”. У відання нового виконавчого органу було передано усі підприємства й організації колишнього Комітету геодезії та картографії СРСР, розташовані на той час на території України (загалом 12 підрозділів).

У листопаді 1992 р. Кабінет Міністрів України прийняв постанову № 622, якою затвердив “Положення про Головне управління геодезії, картографії та кадастру”.

У грудні 1998 р. Верховна Рада України ухвалила закон “Про топографо-геодезичну та картографічну діяльність”. Але тільки 3 червня 1999 р. указом Президента України за № 606/99 затверджено “Положення про Головне управління геодезії, картографії та кадастру”. Відповідно до цього положення Головне управління геодезії, картографії та кадастру (Укргеодезкартографія) є центральним органом виконавчої влади, підпорядкованим Кабінету Міністрів України. Станом на 2010 р. Головне управління підпорядковувалось Міністерству екології та природних ресурсів України.\

Основне завдання Укргеодезкартографії – забезпечити реалізацію державної політики в галузі топографо-геодезичної і картографічної діяльності, здійснення контролю у цій сфері, керівництво, організацію і координацію астрономо-геодезичних, геодезичних, топографічних, маркшейдерських, гравіметричних, картографічних робіт тощо.

Укргеодезкартографія відповідно до покладених на неї завдань:

1) розробляє проекти державних програм щодо забезпечення потреб України в топографо-геодезичній та картографічній продукції;

2) координує топографо-геодезичну і картографічну діяльність в Україні, здійснює методичне керівництво роботами в цій сфері;

3) аналізує стан Державної геодезичної мережі, охорони геодезичних пунктів, розробляє пропозиції щодо єдиної державної системи координат та порядок введення місцевих координат;

4) виступає державним замовником науково-дослідних та інших робіт в галузі, розробляє напрями і програми діяльності в межах своєї компетенції;

5) здійснює державний контроль за додержанням встановлених вимог до виконання робіт, заданих інструктивними документами;

Кабінет Міністрів України постановою № 37 від 16.01.2003 р. затвердив Державну програму науково-технічного розвитку топографо-геодезичної діяльності та національного картографування на 2003–2010 рр.

Основними завданнями програми є:

1. Створення національної системи відліку, пов’язаної з європейськими та світовими системами координат.

2. Розвиток мережі постійнодіючих перманентних станцій супутникових радіонавігаційних спостережень.

3. Модернізація та розвиток державних геодезичної та гравіметричної мережі.

4. Згущення та оновлення Державної нівелірної мережі.

5. Моніторингові дослідження на геодинамічних полігонах і територіях інтенсивного техногенного (антропогенного) навантаження для запобігання сейсмічним та іншим небезпечним процесам.

Головному управлінню підпорядковано виробничі, науково-дослідні, експериментально-виробничі установи, науково-виробничі інститути та інші підприємства. Геодезичні підприємства є майже в кожному обласному центрі.

Геодезичні підприємства є потужними виробничими підрозділами, які

поділені на загони та виробничі ланки, що отримали назву партій.

81. Загальна площа поверхні Землі – 510 млн. км2. Поверхня океанів займає 71 %, а суші 29 % від усієї поверхні Землі. Тому можна вважати, що суша має вигляд невеликого і невисокого плоскогір’я над рівнем океанів порівняно з їхньою глибиною. Оскільки поверхня Світового океану займає майже 3/4 усієї поверхні Землі, її можна прийняти за фігуру Землі, а поверхні суші та дна океанів можна вивчати відносно поверхні Світового океану

Поверхню води в океані в спокійному, незбуреному стані , уявно продовжена під материками так, щоб вона перетинала прямовисні лінії під прямим кутом, називають рівневою поверхнею і приймають за загальну фігуру Землі. Цю фігуру німецький фізик і математик І.Б. Лістінг у 1873 р. назвав геоїдом.

Фігура геоїда залежить від розподілу мас в середині землі і відповідно, від значення сил ваги в кожній точці земної поверхні. Отже, геоїд і фізична поверхня Землі – це складні фігури, які не можна описати будь-якими математичними поверхнями. Але поверхня геоїда все ж таки є згладженішою порівняно з фізичною поверхнею Землі. Тому можна

замінити поверхню геоїда деякою допоміжною поверхнею, яка найбільш наближена до геоїда. Найближчою до геоїда є математична поверхня еліпсоїда обертання. Розміри еліпсоїда задають двома параметрами – великою піввіссю а та геометричним стисненням α . Можна записати формулу α= a-в/а , (І.1.3)

з якої за відомими параметрами а і α легко знайти малу піввісь еліпсоїда в .

Загальноземний еліпсоїд – це еліпсоїд обертання, зорієнтований у тілі Землі так, що його центр збігається з центром мас Землі, площина його екватора – з площиною екватора Землі, і сума квадратів відхилень від поверхні геоїда є мінімальною.

Референц-еліпсоїд – це еліпсоїд, що найкраще описує фігуру Землі для певної території (країни). У різних країнах вчені на основі градусних вимірювань отримали різні розміри референц-еліпсоїдів.

До середини ХХ століття в Україні використовували еліпсоїд Бесселя. В 1940 р. професори Ф.Н. Красовський та О.О. Ізотов отримали розміри еліпсоїда, які найкраще підходили для території СРСР. Еліпсоїд назвали еліпсоїдом Красовського і офіційно прийняли в СРСР у 1946 р. Еліпсоїд Красовського і дотепер використовується в Україні. Пізніше виявилось, що цей еліпсоїд близький до міжнародного еліпсоїда отриманого методами космічної геодезії.

З появою методів космічної геодезії, таких як лазерна локація Місяця та штучних супутників Землі, а також інтерферометрів з наддовгими базисами, які гарантують точність 1–2 см на віддалях до 5000 км, з’явилась реальна можливість точніше визначити параметри не тільки референц-еліпсоїдів, але й загальноземного еліпсоїда. Ці можливості почали реалізовуватись, коли з’явилась нова техніка – GРS

82. Координати точок – це числа, які визначають положення точок на лінії, площині, поверхні або в просторі.

В топографії, як і в геодезії, користуються системами координат, що визначають положення точки на площині, на криволінійних поверхнях та в просторі. в топографії застосовується не

ліва, а права система прямокутних координат.

Щоб визначити положення будь-якої точки, наприклад, точки A , відносно осей координат, опускають з неї на обидві осі перпендикуляри Am і Am1 (Відрізки осей координат Om – абсциса і Om1 – ордината визначають положення точки A на

площині. Їх позначають відповідно AX та УА. Для того щоб кожній парі чисел X та У відповідала на площині одна і тільки одна точка, прийнято значення координат записувати зі знаками плюс чи мінус.

Доволі широко використовують у топографії полярну систему координат на площині. Полярні координати – це полярна віддаль точки від фіксованого початку координат та полярний кут між вибраною полярною віссю і напрямом на точку.

На рис. І.1.14 точка P – полюс, PN – полярна вісь, α – полярний кут,

S – горизонтальна віддаль від полюса P до точки A . Отже, точка A має

координати: кут α та віддаль S . За полярну вісь на площині часто приймають

напрям, паралельний до осі абсцис прямокутної системи координат.

Як відомо, в топографії використовують такі поверхні, як: куля, еліпсоїд,

геоїд (квазігеоїд). Залежно від цього координати поділяють на географічні

(сферичні) – на кулі; геодезичні – на еліпсоїді; астрономічні – на геоїді.

Геодезичною широтою B точки M називається кут, утворений

площиною екватора ECDE′ і нормаллю MK .

Геодезичною довготою L точки M називається двогранний кут між

площиною початкового меридіана PCP′ та площиною меридіана PM ′DP′ , що

проходить через точку M .

Широти точок, розташованих у північній півкулі, називають північними, а

широти точок південної півкулі – південними.

Залежно від того, де розташовані точки – на схід чи на захід від

початкового меридіана, вони мають східні або західні довготи відповідно.

Щоб перейти від геодезичних координат до астрономічних, потрібно

еліпсоїд замінити геоїдом, а нормаль до еліпсоїда – прямовисною.

Астрономічна широта – це кут між площиною екватора та прямовисною лінією у певній точці.

Астрономічна довгота – це двогранний кут між площиною початкового меридіана та площиною астрономічного меридіана цієї точки. Площина астрономічного меридіана – це площина, що проходить через лінію виска в певній точці й паралельна до осі обертання Землі.

У геодезичних роботах різницею між астрономічними і геодезичними

координатами ніколи не нехтують. Ця різниця, спричинена відхиленнями прямовисних ліній і неправильним вибором розмірів та орієнтування референц-еліпсоїда в тілі Землі, є предметом вивчення вищої геодезії.

У географії за фігуру Землі звичайно приймають кулю й нехтують відхиленням прямовисних ліній. В результаті астрономічна та геодезична системи координат перетворюються на єдину географічну систему координат. Прямовисні лінії й нормалі збігаються і стають радіусами, які перетинаються в центрі кулі.

Абсолютна висота точки місцевості назив. відрізок прямовисної лінії від точки на фізичній поверхні до рівневої поверхні.

Перевищення – різниця висот двох точок. Це відстань по прямовисній лінії між рівневими поверхнями через дані точки.

Якщо за рівневу поверхню приймають будь яку іншу, а не вихідну поверхню то висоти точок визначені відносно такої поверхні називають умовним.

83. Як відомо, положення точок земної поверхні на сфероїді визначається геодезичними координатами, а на карті і плані – за допомогою плоских прямокутних координат. Щоб встановити зв’язок між геодезичними та прямокутними координатами застосовують особливий спосіб проектування земної кулі на площину по частинах - поперечно-циліндричну проекцію Гауса-Крюгера.

Проекція Гауса-Крюгера – це проекція поверхні еліпсоїда на площину для опрацювання геодезичних вимірювань і визначення взаємного положення точок цієї поверхні в системі плоских прямокутних координат. Тобто дана проекція дає можливість перерахувати геодезичні координати в прямокутні.

Для топографічних карт масштабів 1:10000 і дрібніших різниця довгот суміжних

меридіанів зони прийнята саме 6⁰

При використанні проекції Гауса-Крюгера земний еліпсоїд поділяють меридіанами, починаючи від 180^о проти годинникової стрілки на сфероїдні двокутники - 6º меридіанні смуги. Зображення такої смуги на площині утворює 6º координатну зону. Кожній зоні відповідає своя колона, тобто N_з = N_к – 30. Середній меридіан в кожній зоні називається осьовим. Напрям осьового меридіану приймається за вісь абсцис, а вісь ординат збігається з відображенням екватора. Умовно початок координат в кожній зоні переносять на 500 км на захід, так щоб всі У в зоні мали додатні значення

Довготу осьового меридіана L₀ шестиградусної зони обчислюють за формулою L₀=6⁰n-3⁰

Х – це відстань в км від екватора до даної точки.

У – містить 4-5 значущих цифр: перші 1-2 – це номер зони, три останні - відстань в км від умовного початку координат

Тому для великомасштабних планів застосовують аналогічну зональну проекцію Гаусса–Крюгера, але з триградусними зонами.

На картах, побудованих у проекції Гаусса–Крюгера, можна визначити сферичні геодезичні координати (широту В та довготу L) будь-якої точки земної поверхні.

Однак використання сферичних координат не є достатньо простим. Тому на топографічних картах у проекції Гаусса–Крюгера, будують особливу координатну сітку, яка забезпечує просте, доволі точне визначення плоских прямокутних координат. Така сітка квадратів називається кілометровою.

Для однозначності приймають, що в кожній зоні ордината осьового меридіана кожної зони дорівнює 500 км, тобто значенню ординати точки O Y0 = 500 км. Тоді точки, розташовані на захід і на схід від осьового меридіана, матимуть додатні значення ординат. Такі координати називаються перетвореними.

На аркушах карт масштабів 1:25000, 1:10000, 1:5000 лінії координатної сітки прокреслюють через 1 км, на аркушах карт масштабів 1:100000, 1:50000 через 2 км, а на аркушах дрібніших масштабів – через 10 км Повні абсциси підписують на вихідних крайніх лініях цього аркуша; усі інші лінії підписують двома останніми цифрами числа.

Крім того, на карті викреслюють мінутну рамку (затемнені та світлі відрізки). Вона дає змогу визначати на карті геодезичні координати B та L. Щоб знайти ці координати точки , проводять на карті найближчу для цієї точки південну паралель (з’єднані однакові мінути на західній і східній сторонах рамки). Проводять також найближчий до точки західний меридіан. Для визначення десятих часток мінути широти та довготи необхідно виміряти відрізки від точки К до проведених паралелі та меридіана, тобто до точок К1' і К2' , і порівняти ці відрізки з відрізками, що відповідають одній цілій мінуті (з темними або світлими мінутними відрізками): скільки десятих частин вони становлять порівняно з однією мінутою.

Отже, за допомогою проекції Гаусса встановлено зв'язок між географічними координатами точок земної поверхні та прямокутними координатами їхнього зображення на площині.

101. На аркуші карти підписані геодезичні координати - широти та довготи вершин рамки трапеції*. Щоб визначити на карті широту точки необхідно через точку провести лінію, паралельну до північної або південної рамки. У точці перетину паралелі з мінутною рамкою карти слід відраховувати значення широти.

Геодезична широтаВ – це гострий кут, утворений нормаллю до поверхні еліпсоїда і площини екватора. Геодезичні широти відлічують від площини екватора в межах 0º - ± 90º. Для точок північної півсфери вони додатні, для південної - від’ємні.

Геодезична довгота L - це двогранний кут, утворений площиною початкового меридіана і площиною меридіана, що проходить через задану точку. Геодезичні довготи, відлічувані від площини початкового меридіана на схід в межах 0º - + 180º, називають східними, а на захід – західними.

Для визначення довготи точки належить через точку провести лінію, паралельну до західної або східної рамки. В точці перетину лінії з мінутною рамкою карти слід відраховувати значення довготи.

102. . Прямокутні координати точок А, В (Х_А, У_А, Х_В, У_В) (див. Рис.3.1.) визначають відносно ліній кілометрової сітки, причім “Х” – віддаль в кілометрах від площини екватора до шуканої точки; “У” – має 4-5 значущих цифр: перші 1 або 2 цифри – це номер зони, три останні - відстань в км від умовного початку координат

103. При розв'язуванні цієї задачі спочатку визначають і підписують на схематичному рисунку висоти двох суміж­них горизонталей, між якими знаходиться точка D. Потім проводять найкоротшу пряму лінію через точку D між двома суміжними горизонталями (рис.4.1а).

а)

Горизонталь з позначкою 245м, на якій лежить точка N, назива­ється молодшою, а горизонталь з позначкою 247,5 м, на якій ле­жить точка М - старшою.

Взаємне розміщення точок N, D і М показано на рис.4.1.

Точкам D і М на карті відповідає їх просторове положення D' і M`. З рис.4.1.б. запишемо шукану висоту Н_D':

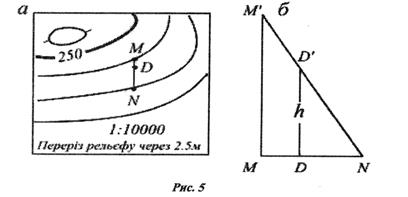_D' = Н_N + h, (4.1)

де h - перевищення точки D' над точкою N.

Таким чином, розв'язування задачі зводиться до обчислення h.

З подібних трикутників ММ'N і DD'N запишемо відношення

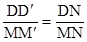, (4.2)

звідки

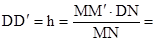____________ м (4.3)

Зауважимо, що ММ' - це переріз рельєфу і в даному випадку дорівнює 2,5 м. У подальшому необхідно виміряти на карті відрізок DN і MN. Ці вимірювання виконують за допомогою циркуля - вимірника з точністю до 0,1 мм.

Обчислюють h з точністю до 1см, тобто до двох знаків після коми.

Н _D = Н_N + h= ____________ м

104. Крутизною схилу називають вертикальний кут v, утворений напрямом схилу і рівневою поверхнею

Щоб спростити визначення крутизни схилів і похилів місцевості використовують спеціальний графік, який називають графіком закладень.
Для побудови графіка закладень горизонтальну лінію ділять на однакові відрізки довільної довжини і на кінцях відрізків підписують значення кутів нахилу, починаючи від 0°30' і далі 1°, 2°, ... до 10°. Потім обчислюють закладення, які відповідають кожному значенню кута нахилу для прийнятої висоти перерізу рельєфу, за формулою d=hctgv.

Для зручності побудови графіка закладень складають допоміжну таблицю, в якій виконано обчислення для h . В останній графі таблиці одержано значення d (в см), які і необхідно відкласти на графіку закладень.
Одержані величини закладень, виражені у масштабі карти, відкладають на перпендикулярах до горизонтальної лінії проти відповідних кутів нахилу. Через верхні кінці перпендикулярів проводять плавну криву за допомогою лекала.
Щоб визначити крутизну схилу за графіком закладень, циркулем-вимірником беруть на схилі відстань АВ між двома сусідніми горизонталями і прикладають до графіка закладень так, щоб одна ніжка циркуля знаходилась на горизонтальній лінії, а друга – на кривій.

На горизонтальній лінії графіка читають крутизну схилу в градусах.

При виконанні задачі на креслярському папері за допомогою чорної туші будують графік закладень для кутів нахилу 0°30', 1°, 2°, 3°, 4°, 5°, 10°, 20° і висоті перерізу рельєфу для даної топографічної карти. Обчислені значення закладень показують в зошиті у вигляді таблиці.

105. Зображення розрізу місцевості вертикальною площиною називається профілем. Для цього необхідно на карті з'єднати прямою лінією вихідні пунктиі підписати на карті позначки горизонталей, які перетинає . Точки перетину лінії з цими горизонталями послідовно нумерують числами 1, 2, 3 і т.д. Точки перетину прямої з іншими об’єктами(ліси, сади,тощо позначають 1’,2’,3’ і т.д.

Побудована лінія буде основою профілю. Перпендикулярну до неї лінію оцифровують відповідно до значень висот горизонталей. Вертикальний масштаб, зазвичай, приймають таким, щоб одному сантиметру відповідало значення перерізу рельєфу.

Наступним етапом розв'язування задачі є побудова профілю. У кожній з позначених на горизонтальній осі точці відкладають вер­тикально відрізок, який відповідає висоті кожної з цих точок. Значення висот точок знаходять на карті.

Нанесені на сітку профілю точки з'єднують плавною лінією.

Якщо у напрямку лінії побудови профілю є лісові масиви чи насадження, необхідно побудувати на профілі у відповідному місці схематичне зображення цього масиву, від­клавши вертикально середню висоту дерев цього лісу відповідно до прийнятого вертикального масштабу профілю.

Закінченням графічної побудови цієї задачі буде з'єднання на профілі просторових положень крайніх точок. Бажано цю лінію на профілі показати червоним кольором. Після виконання всіх описаних побудов, можна зробити висновок щодо взаємної видимості між пунктами.

106. Для розв’язування цієї задачі скористаємося формулою i₀ = h / d₀ ,де d₀ - горизонтальна проекція лінії, яка відповідає заданому ухилу і₀ при даному перерізі рельєфу h.

Потім отриману величину d₀ визначаємо в масштабі карти.

Розхилом циркуля-вимірювача на величину d₀ в масштабі карти, прокладаємо лінію заданого ухилу між точками.

Одну з ніжок циркуля ставлять у першу точку , а другою ніжкою циркуля засікають точку 1 на суміжній горизонталі в напрямі другої точки . Із точки 1 аналогічно засікають на наступній суміжній горизонталі точку 2, далі із точки 2 - точку 3 і т.д. до кінцевої точки.

У місцях з пологим рельєфом, де віддаль між сусідніми горизонталями більша d₀ проектована лінія може розміщуватись вільно в напрямі на кінцеву точку ходу.

107. Крутизною схилу називають вертикальний кут v, утворений напрямом схилу і рівневою поверхнею

Щоб спростити визначення крутизни схилів і похилів місцевості використовують спеціальний графік, який називають графіком закладень.
Для побудови графіка закладень горизонтальну лінію ділять на однакові відрізки довільної довжини і на кінцях відрізків підписують значення кутів нахилу, починаючи від 0°30' і далі 1°, 2°, ... до 10°. Потім обчислюють закладення, які відповідають кожному значенню кута нахилу для прийнятої висоти перерізу рельєфу, за формулою d=hctgv.

Для зручності побудови графіка закладень складають допоміжну таблицю, в якій виконано обчислення для h . В останній графі таблиці одержано значення d (в см), які і необхідно відкласти на графіку закладень.
Одержані величини закладень, виражені у масштабі карти, відкладають на перпендикулярах до горизонтальної лінії проти відповідних кутів нахилу. Через верхні кінці перпендикулярів проводять плавну криву за допомогою лекала.
Щоб визначити крутизну схилу за графіком закладень, циркулем-вимірником беруть на схилі відстань АВ між двома сусідніми горизонталями і прикладають до графіка закладень так, щоб одна ніжка циркуля знаходилась на горизонтальній лінії, а друга – на кривій.

На горизонтальній лінії графіка читають крутизну схилу в градусах.

При виконанні задачі на креслярському папері за допомогою чорної туші будують графік закладень для кутів нахилу 0°30', 1°, 2°, 3°, 4°, 5°, 10°, 20° і висоті перерізу рельєфу для даної топографічної карти. Обчислені значення закладень показують в зошиті у вигляді таблиці.

108. Виміряти величину - це значить порівняти її з іншою величиною, прийнятою за одиницю міри. Процес вимірювання неминуче супроводжується похибками. Отже, в результаті вимірювань спостерігач отримує не істинну величину, а лише наближене значення фізичної величини.

За характером похибки поділяють на два класи:

1. грубі;

2. неминучі

· систематичні

· випадкові

До грубих похибок відносяться ті, які виникають внаслідок недбалого проведення вимірювального процесу - прорахунки у вимірах, викликані неуважністю спостерігача, несправністю приладу та ін. Грубі похибки виключаються із результатів вимірювань, переважно, проведенням повторних вимірювань або іншою методикою.

Систематичні похибки виникають з визначеного джерела та мають визначений знак та величину. Ці похибки підкоряються відомим математичним законам та можуть бути враховані або зведені до мінімуму.

Випадкові похибки неминучі та завжди супроводжують вимірювання. Закономірності випадкових похибок можна виявити в масиві вимірів та обумовлені точністю приладу, кваліфікацією спостерігача та іншими факторами. Їх вплив може бути послаблено, підвищуючи якість та число вимірів, а також виконуючи належну математичну обробку результатів вимірювань.

Під випадковою похибкою ∆i розуміють різницю між вимірюваним значенням випадкової величини хі та точним значенням Х, тобто ∆=− ii xX, де і=1,2,…, п

109. Виміряти величину - це значить порівняти її з іншою величиною, прийнятою за одиницю міри. Процес вимірювання неминуче супроводжується похибками. Отже, в результаті вимірювань спостерігач отримує не істинну величину, а лише наближене значення фізичної величини.

За джерелом походження розрізняють такі види похибок:

• особисті похибки спостерігача;

• інструментальні похибки;

• похибки методу вимірювань;

• похибки за вплив зовнішнього середовища.

Похибки методу вимірювання - спричинені недосконалістю цьо­го методу, а також недостатністю обгрунтування С його теорії, засто­суванням наближених формул для спрощення розрахунків тощо.

Інструментальні похибки - складова похибок вимірювання - зу­мовлена недосконалістю засобів вимірювальної техніки. Ця похибка також може бути обумовлена конструктивними та технологічними недоліками. Наприклад, через неточність виготовлення та нестабільно­сті елементів засобів вимірювальної техніки, неправильне градуюван­ня шкали приладу тощо.

Суб'єктивні (особисті) похибки - як правило, є наслідком особи­стих властивостей спостерігача (експериментатора), які зумовлені осо­бливостями його організму (недосконалість зору, втомленість тощо).

110. Властивості випадкових похибок вимірювань проявляються в масивах вимірів. Їх характеристики такі:

а) властивість обмеженості: випадкові похибки за абсолютним значенням для заданих умов вимірювань не перевищують визначеної межі |∆| ≤ ∆гр;

б) властивість симетричності: додатні та від’ємні значення похибки рівноможливі та за більшої кількості вимірювань однаково часто виникають;

в) властивість унімодальності: малі за абсолютним значенням випадкові похибки виникають у разі вимірювань частіше, ніж великі;

г) властивість компенсації: середнє арифметичне із значень випадкових похибок за нескінченного зростання кількості вимірювань прямує до нуля, тобто володіє властивістю компенсації

lim[∆]/n→0

n→∞

Якщо не виконується остання властивість, то похибки відносять до систематичних

Арифметична середина та її властивості.

Відомо, що найнадійнішим (ймовірним) значенням багаторазово виміряної величини S є середнє арифметичне із результатів вимірювань або проста арифметична середина

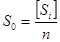
Це пояснюється такими її властивостями:

• Якщо кількість вимірів велика, середнє арифметичне прямує до істинного значення

lim[Sі]/n→Sіст.

n→∞

• Сума відхилень виміряних значень Sі від середнього арифметичного So дорівнює нулю

[ν] = 0, (І.3.55)

де vі = So – Sі.

Коли вимірювання рівноточні і за найімовірніше значення виміряної величини приймають середнє арифметичне, середню квадратичну похибку одного вимірювання mS визначають за формулою Бесселя

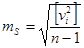де vі – відхилення окремих вимірів від середнього арифметичного; n – кількість вимірів.

Середню квадратичну похибку M S арифметичної середини обчислюють

за формулою