Внутри потока. Математическое осознание того, что в теории струн есть не только струны, но также и браны, оказало огромное влияние на исследования в этой области. Бранный

Математическое осознание того, что в теории струн есть не только струны, но также и браны, оказало огромное влияние на исследования в этой области. Бранный сценарий и сопутствующие ему мультивселенные составляют направление исследований, которое потенциально может привести к значительному пересмотру наших представлений о реальности. Без точных математических методов, разработанных за последние полтора десятка лет, значительная часть этих открытий осталась бы за пределами наших возможностей. Однако основная проблема, которую физики надеялись решить с помощью точных методов, — выбор единственной формы пространства дополнительных измерений из многих кандидатов, выявленных теоретическими исследованиями, — пока остаётся нерешённой. Мы по-прежнему далеки от её решения. На самом деле, новые методы только усугубили проблему. Было открыто огромное количество новых видов пространств дополнительных измерений, что привело к невероятному увеличению числа возможных кандидатов, а понимание того, как выбрать одно единственное пространство, не продвинулось ни на йоту.

Ключевым для этих исследований явилось наличие у бран важной характеристики — потока . Подобно электрону, порождающему электрическое поле — электрический «туман», заполняющий пространство вокруг него, или подобно магниту, порождающему магнитное поле — магнитный «туман», заполняющий пространство вокруг него, брана порождает бранное поле — бранный «туман», заполняющий пространство вокруг неё (рис. 5.5). Когда в 1800-х годах Фарадей проводил первые эксперименты с электрическими и магнитными полями, для измерения напряжённости поля он использовал плотность силовых линий поля, расположенных на заданном расстоянии от источника, и эту величину он назвал потоком поля. С тех пор этот термин прочно вошёл в обиход. Напряжённость поля браны тоже измеряется порождаемым ей потоком.

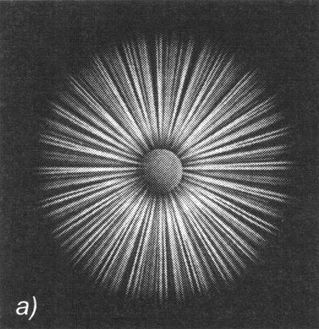
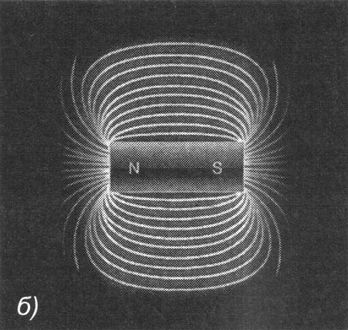
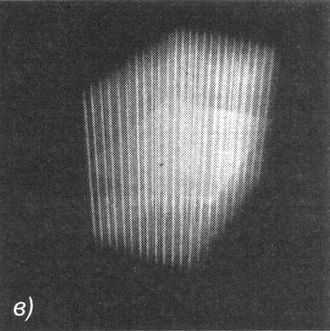
Рис. 5.5. а ) Электрический поток, порождённый электроном; б ) Магнитный поток, порождённый магнитным стержнем; в ) Бранный поток, порождённый браной

Струнные теоретики, среди которых Рафаэль Буссо, Польчински, Стивен Гиддингс, Шамит Качру и многие другие, осознали, что для полного описания дополнительных измерений теории струн требуется не только определить их форму и размер — то, чем исследователи в этой области, включая меня, занимались в 1980–1990-х годах, — но также определить пронизывающие их потоки созданных бранами полей. Позвольте мне чуть более подробно остановиться на этом.

Со времён появления первых математических работ по дополнительным измерениям теории струн исследователям было известно, что пространства Калаби–Яу, как правило, содержат много пустых полостей, подобно пространству внутри мяча, внутри бублика или внутри фигурки из дутого стекла. Так продолжалось до тех пор, пока в самом начале нового тысячелетия теоретики не осознали, что пустые полости могут чем-нибудь заполняться. Они могут быть обёрнуты теми или иными бранами и пронизаны создаваемыми ими потоками полей (рис. 5.6). В более ранних исследованиях (кратко сформулированных, например, в «Элегантной Вселенной») по большей части рассматривались только «голые» пространства Калаби–Яу, для которых подобного рода украшения отсутствуют. Когда учёные осознали, что на пространства Калаби–Яу могут быть «навешены» дополнительные свойства, они обнаружили гигантский набор модифицированных пространств дополнительных измерений.

Рис. 5.6. В теории струн браны могут наматываться на часть дополнительных измерений, эти измерения могут быть пронизаны потоками созданных бранами полей — в результате получаются «одетые» пространства Калаби–Яу. (На рисунке представлена упрощённая версия пространства Калаби–Яу, «бублик с тремя дырками». Схематично показаны намотанные браны и линии потока в виде жгутов, намотанных на определённые части пространства)

Даже грубый подсчёт даёт представление о масштабе. Рассмотрим поток. Так же как в квантовой механике устанавливается, что число фотонов и электронов всегда целое — может быть 3 фотона и 7 электронов, но не 1,2 фотона или 6,4 электрона, — точно так же квантовая механика доказывает, что силовые линии потока собираются в целочисленные пучки. Они могут пронизывать охватывающую поверхность один раз, два раза, три раза и так далее. В принципе, помимо требования целочисленности, других ограничений не существует. На практике, когда количество линий в потоке велико, он стремится исказить пространство Калаби–Яу, что делает использованные ранее математические методы неточными. Во избежание попадания в этот математический омут учёные, как правило, рассматривают потоки с количеством линий не более 10, а часто и того меньше.59

Это означает, что если данное пространство Калаби–Яу содержит одну пустую полость, то её можно одеть потоком десятью разными способами, что приведёт к десяти новым пространствам дополнительных измерений. Если данное пространство Калаби–Яу имеет две такие полости, то имеем 10 × 10 = 100 различных способов одеть поток на пространство (10 возможных потоков на первую полость и 10 на вторую); если три пустые полости — имеем 103 различных способов одеть поток на пространство, и так далее. Насколько большим может быть это число? Некоторые пространства Калаби–Яу имеют порядка пятисот пустых полостей. Рассуждая аналогично, получаем, что число различных форм пространств дополнительных измерений будет порядка 10500.

Таким образом, вместо того чтобы просеять кандидатов и отобрать из них несколько выделенных пространств дополнительных измерений, точные математические методы открыли целый рог изобилия новых возможностей. Совершенно неожиданно выяснилось, что число возможных нарядов пространств Калаби–Яу значительно превышает число частиц в наблюдаемой части Вселенной. Для некоторых струнных теоретиков такой вывод стал большим разочарованием. Как подчёркивалось в предыдущей главе, не имея какого-нибудь способа выбрать точный вид дополнительных измерений — который, как мы теперь знаем, дополнен также выбором одетого на пространство потока, — математический аппарат теории струн лишается своей предсказательной силы. Так много надежд возлагалось на математические методы, которые могут работать вне рамок теории возмущений. Теперь же, когда некоторые из этих методов были реализованы, проблема фиксации формы пространства дополнительных измерений только усугубилась. После этого некоторые струнные теоретики совсем приуныли.

Другие, более жизнерадостные, верят, что сдаваться ещё рано. Однажды — возможно совсем скоро, а может и нет — будет найден недостающий принцип, определяющий вид дополнительных измерений, включая конкретный поток, в котором будет щеголять та или иная форма.

Иные теоретики придерживаются ещё более радикальной точки зрения. Возможно, говорят они, за десятилетиями бесплодных попыток установить точную форму пространства дополнительных измерений стоит некий смысл. Возможно, совершенно вызывающе продолжают эти радикалы, необходимо рассматривать все возможные формы и потоки, возникающие в математическом аппарате теории струн. Возможно, настаивают они, причина, по которой математика наполнена этими возможностями, в том, что они все реальны , каждая из форм задаёт дополнительные измерения в своей отдельной вселенной. И может быть, усмиряя необузданный полёт фантазии наблюдательными фактами, именно это и необходимо для рассмотрения самого трудного, по всей видимости, вопроса — космологической постоянной.