Аспан денелерінің ара қашықтығын анықтау 4 страница

Сондықтан, планета Жерден қалып отырады да, кері бағытта баяу қозғалғандай болады. Төменгі планеталар төменгі қосылуының (V₁) маңайында (4-сурет) жұлдыздар арасында кері бағытта қозғалады, ал жоғарғы қосылуының (V₃) маңайында тура бағытпен қозғалады.

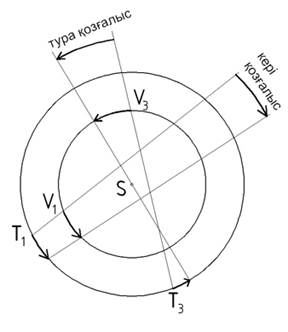Планеталардың Күнді толық бір айналуына кеткен уақыт аралығы сидерлық (сидерикалық) период Т деп аталады.

Жердің сидерлық периоды жұлдыздық жылға тең болады 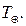Планеталардың сидерлық периоды, синодтық периоды және жұлдыздық жыл арасында жай математикалық байланыс бар. Планетаның орбита бойынша сөткелік бұрыштық қозғалысы 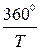тең, ал Жердің тәулік-тік бұрышқтық қозғалысы 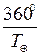бола-

4-сурет. Ішкі планетаның көрінерлік қозғалысын түсіндіру

ды. Планета мен Жердің тәуліктік бұрыштық қозғалыстарының айырымы

планетаның бір тәуліктегі бұрыштық көрінерлік қозғалысын береді, ал ол 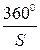тең болады. Сондықтан,

Төменгі планеталарға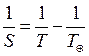

Жоғарғы планеталарға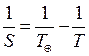

Мұндағы S – синодтдық айналу периоды,

Т – сидерлық айналу периоды,

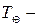жұлдыздық жыл.

Бұл теңдеулер синодтық қозғалыстың теңдеуі деп аталады. Бақылаудан планеталардың синодтық (S) периоды анықталып, сидерлық (T) периодтарын осы теңдеулерден есептейді.

Сұрақтары: 1. Әлемнің құрылымы туралы көзқарастың дамуы. 2.Күн жүйесінің кинематикасы. 3.Астрономияның пайда болуы.4. Ежелгі халықтардың әлем туралы көзқарасы. 5.Планеталардың көзге көрінер қозғалысы. 6.Планеталардың символикасы. 7.Ежелгі Грециядағы астрономияның дамуы. Пифагор, Аристотель; Гиппарх; Птолемей. 8.Әлемнің геоцентрлік жүйесі. 9.Орта Азияда астрономияның дамуы. Бируни және Улугбектің еңбектері. 10.Планеталардың конфигурациялары. 11.Коперник және оның әлемдік Гелиоцентрлік жүйесі. 12.Синодикалық қозғалыстың теңдеуі. 13.Коперник түсіндірген планеталардың тұзақты қозғалысы. 14.Гелиоцентризм үшін талас. Бруно, Галилей, Ломоносов.

8-ші лекция. Күн жүйесінің кинематикасы. Тихо Браге, Кеплер және планеталардың қозғалыс заңдары. Кәзіргі көзқарас бойынша күн жүйесінің құрылысы.

Планеталардың қозғалыс заңдылықтарын XVII ғасырдың басында әйгілі неміс математигі Иоганн Кеплер ашқан. Қазіргі кезде Кеплердің эмпирикалық заңдары былай оқылады:

1. Барлық планеталар эллипстер бойымен қозғалады. Осы эллипстердің жалпы бір фокусінде Күн орналасады.

2. Планеталардың радиус-векторлары тең уақыт аралықтарында тең аудандар сызады.

3. Планеталардың сидерлық периодтарының квадраттары олардың орбиталарының үлкен жарты остерінің кубтеріне пропорционал болады.

5-сурет. Эллипстық орбита

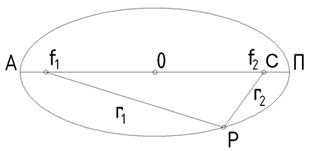Эллипстің кез-келген нүктесі-нің екі қозғалмайтын үлкен остің бойында жататын ( 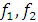– 5-сурет) және фокустер деп аталатын нүктелерден ара-қашықтардың қосындысы тұрақты және үлкен остің шамасына тең болады.

r₁+r₂=2a=AП

а – үлкен жарты остің шамасы,

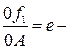эксцентриситет. Шеңбердің эксцентриситеті 0-ге тең.

Планеталардың орбиталарының формалары шеңберге жақын. Венераның орбитасының эксцентри-ситеті 0,007, Жердікі 0,017.

Күн С нүктесінде орналассын делік. Орбитаның күнге ең жақын нүктесі П перигелий деп, ал ең алыс нүктесі А афелий деп аталады. Планетаның Күннен перигелийдегі қашықтығы:

q=a (1-e)

афелийдегі қашықтығы:

Q=a (1+e)

Кез-келген уақыт моментіндегі қашықтығы планетаның радиус- векторы 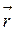мен сипатталады.

Кеплердің екінші заңы бойынша планетаның сызықтық жылдамдығы тұрақты болмайды. Пергелийдегі жылдамдық өзінің максимал шамасына жетеді:

V_q=V_c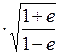

Афелийде – минимал болады:

V_Q=V_C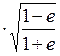

деп белгіленген.

V_c – орташа немесе планетаның шеңберлік жылдамдығы. Жердің шеңберлік жылдамдығы 29,78км/с.

Кеплердің үшінші заңының математикалық формасы:

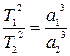
Т₁, Т₂ – сидерлік периодтар;

а₁, а₂ – орбитаның үлкен жарты остері.

Егерде планеталардың орбиталарының үлкен жарты осін Жердің Күннен қашықтығы мен ал сидерлық периодтарын жұлдыздық жылмен есептейтін болсақ, онда Кеплердің үшінші заңы мына түрге келеді:

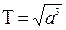
Планетаның (астериод, комета) қозғалысын анықтау үщін олардың орбитасының жазықтығының кеңістіктегі орналасуын, орбитаның өз жазықтығындағы орнын, орбитаның формасын, мөлшерін, және планетаның орбитаның белгілі бір нүктесінде болу моментін (уақытын) білу қажет. Планетаның орбитасын анықтайтын шамалар орбитаның элементтері деп аталады.

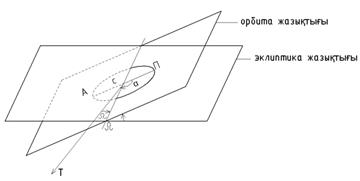Орбитаның кеңістікте орналасуын анықтау үшін негізгі жазықтық ретінде эклиптика /Жер орбитасының жазықтығы/ алынады. /6-сурет/. Екі жазықтықтың қиылысу сызығын – түйін сызығы деп, орбитаның эклиптика жазықтығымен қиылысқан екі

6-сурет. Орбита элементтері

нүктені орбитаның түйіндері деп атайды. Егерде планета оңтүстік жарты сферадан солтүстік жарты сфераға өтетін болса, осы нүктені шығу түйіні 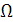деп атайды.

Эллипстік орбитаны мына алты элементтер арқылы анықтайды:

1. 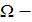шығу түйінінің бойлығы,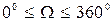

2. 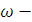перигелийдің шығу түйіннен бұрыштық қашықтығы,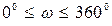

3. 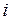– көлбеулік,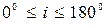

4. 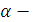үлкен жарты осі,

5. 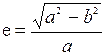– эксцентриситет,

6. 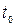– перигелийдің өту моменті.

Сұрақтар: 1.Күн жүйесінің кинематикасы. 2.Тихо Браге, Кеплер және планеталардың қозғалыс заңдары. 3.Кәзіргі көзқарас бойынша күн жүйесінің құрылысы.

9-шы лекция. Тәуліктік параллакс, Күннің параллаксы. Астрономиялық бірлік. Арақашықтықты анықтаудың радиолокациялық әдісі. Күн, Ай және планеталардың өлшемдерін анықтау. Жердің Күнді айнала қозғалуын дәлелдеу: жылдық параллакс, жарық абберациясы.

Бүкіл әлемдік тартылыс заңы бойынша өз осінен баяу айналатын массивті жалғыз дененің формасы шар тәрізді болу керек. Көптеген аспан денелерінің /Күн, Ай, планеталардың/ формалары шарға жақын. Жердің шар тәрізді екені көптеген космостық бақылаулардың нәтижелерінен көруге болады. Жерді осы шар тәрізіділігі оның мөлшерін анықтауға мүмкіндік береді. Бұл әдісті ең бірінші рет б.д.д. ІІІғ. Эратосфен қолданған. Осы әдістің негізі былай түсіндіріледі. Жер бетінде бір географиялық меридианның үстінде жатқан екі нүкте 0₁, 0₂ алынады /10-сурет/.

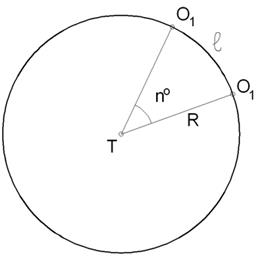Меридианның 0₁0₂ доғасының ұзындығын /мысалы км-мен/ 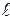деп белгілеп, ал бұрыштық ара қышықтықты 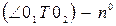дейік. Сонда, меридианның бір градус доғасының ұзындығы 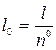болады да ал, толық шеңбердің ұзындығы мынаған тең болады: 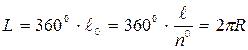. Мұнда R Жердің радиусы. Соңғы өрнектен

	10-сурет. Жер радиусын анықтау

Жердің радиусын септеп шығара аламыз

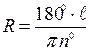
Бұрыштық қашықтық 0₁,0₂ нүктелердің географиялық ендіктерінің айырыма тең болады: .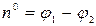

Географиялық ендіктерді белгілі астрономиялық әдістермен табуға болады. Ал, екі нүктенің арасындағы меридианның доғасының ұзындығын тікелей өлшеуге мүмкіншілік болмайды. Себебі бұл нүктелер бір бірінен алыс орналасқандықтан олардың араларында таулар, көлдер, өзендер, сайлар кездесіп отыруы да мүмкін. Сондықтан, доғаның ұзындығын өлшеуге арналған триангуляция әдісі енгізілген. Бұл әдіс бойынша екі нүктенің біреуінің манайында тегіс жерде базис деп аталатын ара қашықтық өлшенеді. Екі нүктенің арасында меридианның екі жағынан көптеген нүктелер алынып, олардың әрбіреуінде геофизикалық сигналдар орнатылып, аспаптардың көмегімен керекті бұрыштар өлшенеді. Меридианның керекті доғасының ұзындығын үшбұрыштардың көмегімен есептейді. 1615ж. бұл әдісті бірінші енгізіп қолданған голланд инженері Снеллиус болатын. Сол уақыттан бері Жердің бетіндегі көптеген доғалар өлшеніп, көптеген ендіктердегі Жердің радиусы анықталған. Осы өлшеулердің нәтижелері бойымен әртүрлі ендіктерде 1⁰ доғаның ұзындығы әртүрлі болды. Экватордағы 1⁰ доғаның ұзындығы 110,6 км, полюстердің манайында 111,7 км. Осыдан Жердің формасы дұрыс шар формалы болмай, сығылған немесе айналған эллипсойдтың /сферойдтың/ формасына жақын келетіндігін көреміз.

Соңғы 1,5 ғасырдың ішінде Жер сферасының элементтері көптеген градустық өлшеулермен қалыптасты. Сферойдтың кіші осі 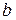Жердің айналу өсіне сәйкес болып, ал үлкен осі а экватор жазықтығында жатады. Сферойдтың сығылуының шамасы үшін мына катынас алынады: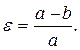

1964ж. Бүкіл халықаралық астрономиялық съезде Жердің эллипсойдының мына элементтерін қабылдаған:

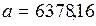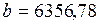км

км

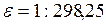
Халықаралық геодезиялық және геофизикалық одақтың XVII ассамблея (Канберра, 1979 жыл) шешімімен жер эллипсоидының жаңа параметрлері енгізілген:

a = 6378136 м, в = 6356751 м, ε = 1 : 298,257

Жердің шын фигурасын сферойдпен де үш ості эллипсойдпен де және белгілі математикалық фигуралармен де үйлестіруге болмайды. Сондықтан, Жердің фигурасы деп оның бетінің /теңіз, мұхиттар физикалық формасы емес, геоидтық бетін айтады. Геоид /немесе геоидтық беті деп/ ашық мұхиттағы тыныштықтағы судың беті. Геоидтық бет Жер эллипсойдының бетіне өте жақын орналасады: материктерде сәл ғана жоғарырақ, ал мұхиттарда төменірек жатады. Екі беттің ең үлкен ара қашықтығы 100 м-дей болады. Жердің жасанды серіктерінің көмегімен Жердің шын формасы зерттеледі. Бұл зерттеулер геоидқа ең жақын орналастын эллипсойдтың элементтерін анықтауға бағытталған болады.

Аспан денелерінің ара қашықтығын анықтау

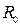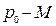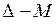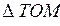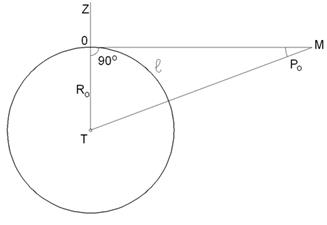
Күн жүйесіне жататын аспан денелерінің қашықтықтарын олардың горизонттық параллакстары арқылы анықтайды. ІІ-суретке Жердің экваторлық радиусы, шырақтың горизонттық экваторлық параллаксы, шырақтың Жердің Т – центрінен қашықтығы. Суреттегі үшбұрышын қарастырып 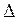ара қашықтықты былай

11-сурет. Горизонттық параллакс

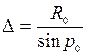табамыз: . Айдан басқа Күн жүйесіндегі денелер-дің горизондтық экваторлық параллакстары аз шама болған-дықтан 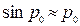/радианмен есептегенде/, немесе 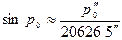/ секундпен есеп-тегенде/ алуымызға болады.

Сонда:

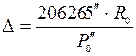
Күн жүйесіндегі аспан денелерінің қашықтығын радиолокация әдісімен де өлшеуге болады. Егер радиосигналдың аспан денесіне барып қайтып оралуына t уақыт кететін болса, осы денеге дейін қашықтық мынаған тең:

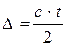
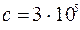км/с – радиотолқындардың жылдамдығы.

Жұлдыздарға дейінгі қашықтықты олардың жылдамдық параллаксы арқылы анықтайды.

Жылдық параллакс деп жұлдыздан Жер орбитасының жұлдыздық бағытына перпендикуляр орналасқан радиусы көрінетін бұрышын айтады.

12-сурет. Жылдық параллакс

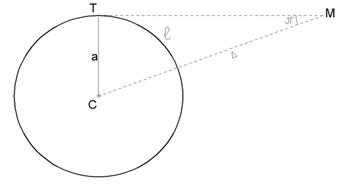12-суретте С – Күн, Т – жер, М – шырақ, а – Жер орбитасының радиусы, 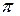– жылдық параллакс, 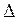–жұлдыздың Күннен қашық-тығы. Осы суреттегі 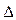СТМ үшбұрышынан қашықтықты анықтауға болады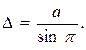

Жұлдыздардың параллакстары 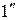аз. Сондықтан, .

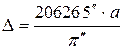Аспан денелерінің қашықтықтары үлкен сандар болғандықтан, оларды километрлермен алу ыңғайсыз. Сондықтан астрономияда мынадай ұзындықтын өлшем бірліктері қабылданған:

астрономиялық бірлік /а.б./ - Жердің Күннен орташа қашықты;

парсек /пк/ - жылдық параллакс 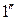-ке сәйкес қашықтық;

жарық жылы /ж.ж./ - жарықтың бір жылда өтетін қашықтығы.