Порядок наблюдений и вычислений

Определить широту по меридиональной высоте Солнца 7 сентября 2001 года.

1. tg ₁ положителен всегда, незавсимо от наименования широты.

2. tg 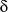положителен, если и 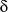одноименны и tg 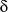отрицателен, если и 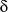разноименны.

3. положительно, если светило приближается к повышенному полюсу, и отрицательно, если светило удаляется от повышенного полюса.
Это официальное правило. Оно сформулировано в "МТ-75" и в учебниках по Мореходной астрономии. Правило требует глубоких знаний по небесной сфере. Чтобы не ошибиться в знаках при практическом решении задачи, рекомендуется использовать следующее правило Мурманского:
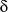Если и одноименны, то знак такой же, как в МАЕ.
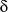Если же и разноименны, то знак противоположный знаку в МАЕ.

4. Часовую разность широт 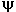можно определить графически на карте, либо выбрать из таблицы 24 МТ-75, либо расчитать по формуле 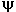= vcosИК. Официальное правило знака часового изменения широты: 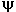положительно, если широта и РШ одноименны, и отрицательно, если широта и РШ разноименны.
Т.к. 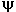чаще всего вычисляют на калькуляторе, то рекомендуется следующее калькулятороное правило:
В северном полушарии знак 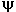такой же, как на калькуляторе, а в южном полушарии знак 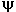противоположен знаку калькулятора.

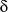Поправку вычисляют на калькуляторе или выбирают из таблицы 19 МТ-75, куда входят с разностями (tg - tg ) и ( - 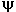). Часовое изменние склонение Солнце <1,0', а при скоростях судов v< 18 узлов часовое изменение широты 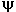<18,0'. Поэтому квадрат второй скобки формулы ( . ) всегда <1. На величину поправки оказывает влияние первая скобка (tg - tg 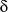). Т.к. склонение Солнца не превосходит 23,5°, то tg <0,44. Следовательно, на величину поправки в основном оказывает влияние величина широты.
Из анализа формулы ( . ), и из таблицы 19 следует, что в малых широтах поправка не превосходит 0,1'-0,2', поэтому эту поправку не учитывают.

В средних широтах поправкой можно пренебречь, если курс близок к параллели. При других курсах поправку надо рассчитать.
И обязательно поправку надо учитывать в высоких широтах, т.к. она может достигать несколько минут.

Определение широты по Полярной звезде.

· Теория метода.

· Порядок наблюдений и вычислений.

· Достоинства и недостатки метода.

Теория метода.

Высота полюса мира над горизонтом всегда равна широте места. К сожалению, в самих полюсах нет звезд, измеряя высоты которых, можно было практически сразу после исправления поправками получать широту. Но недалеко от северного полюса Р_N находится достаточно яркая звезда 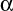Малой Медведицы, называемой Полярной звездой. Координаты Полярной на 2001 г. 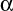= 38°45' и 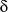= 89°16'. Следовательно, её полярное расстояние = 90° - 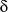< 1° = 44'. Поэтому высота Полярной звезды близка к широте и может отличаться на небольшую величину х.

Пусть Полярная звезда находится в произвольной точке С. Из данной точки опустим сферический перпендекуляр на меридиан наблюдателя. Величина х - есть проекция полрного расстояния на меридиан наблюдателя. Так как полярное расстояние мало (44'), то прямоугольный треугольник P_NCD можно считать плоским.
Из данного прямоугольного треугольника имеем x = cost_м
Из рисунка видно, что = h_o - x (*)
На основании основной формулы времени, имеем x = сos(S_м - ).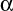
Подставляя в формулу (*) значение х, получаем = h_o - сos(S_м - )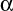
Ведём обозначения I = - _o сos(S_м - 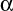_o) (**)
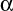_o и _o - среднегодовые значения прямого восхождения и полярного расстояния Полярной звезды.

Окончательно широта по высоте Полярной звезды определяется следующей формулой

= h_o + I + II + III (4.8)

Поправка I учитывает суточное вращение Полярной звезды вокруг северного полюса мира, как видно из формулы (**) зависит только от звездного времени и выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на страницах 277-278.

Поправка II учитывает сферичнось треугольника P_NCD и корректирует поправку I, всегда положительная, выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на странице 279 по аргументам S_м и h.

Поправка III учитывает изменение в течении года экваториальных координат Полярной звезды корректирует поправку I выбирается из МАЕ из таблицы "Широта по высоте Полярной звезды" на странице 280 по аргументам S_м и дата.

И так как все поправки зависят от звездного местного времени, следовательно, для определеня широты по высоте Полярной звезды кроме исправления высот необходимо расчитать звездное местное время, чтобы по этому аргументу выбрать поправки I, II и III.