Автоматизированное проектирование синтеза топологии бортовых систем и кабельной сети наноспутника

Выполнил ________________________________________(Тлеумбет П.В.)

Проверил ________________________________________(Аваряскин Д.П.)

Нормоконтролёр____________________________________(Аваряскин Д.П.)

Самара 2017

Содержание

ВВЕДЕНИЕ……………………………………………………………….…..
ОБЗОР ЛИТЕРАТУРЫ……………………………………………...……….
ЗАКЛЮЧЕНИЕ…………………………………………………………........
СПИСОК ЛИТЕРАТУРЫ………………………………………………...….

ВВЕДЕНИЕ

Актуальность работы. В настоящее время область приминения наноспутников расширяется соответсвенно количество производства наноспутников увеличивается. В связи с этим одним из важных задач в производстве космических аппаратов является ускорение срока. Основным средством ускорения темпов разработки космических аппаратов является автоматизированность проектирования. Под автоматизацией проектирования (АП) понимается такой способ выполнения процесса разработки проекта, когда проектные процедуры осуществляются разработчиком изделия при тесном взаимодействии с ПК. АП предполагает систематическое использование средств вычислительной техники (ВТ) при рациональном распределении функций между проектировщиком и ПК и обоснованном выборе методов машинного решения задач. Рациональное распределение функций между человеком и ПК подразумевает, что человек должен в основном решать задачи творческого характера, а ПК- задачи, допускающие формализованное описание с традиционным ручным способом. В работе исследуется задача разработки алгоритма для синтеза топологии бортовых систем и кабельной сети наноспутника.

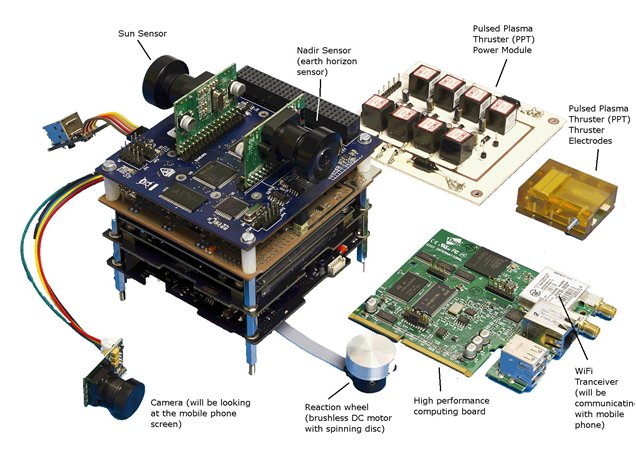
Рисунок 1 – Сборка бортовых систем наноспутника

Целью выпускной квалификационной работы магистра является разработка алгоритма синтеза топологии бортовых систем и бортовой кабельной сети для автоматизированного проектирования бортых систем и бортовой кабельной сети наноспутника.

Для достижения указанной цели в работе решаются следющие задачи:

1. Анализ существующих бортовых систем;

2. Получить топологическую модель БС наноспутника;

3. Разработать алгоритм синтеза топологии БС и БКС наноспутника;

4. Автоматизировать систему проектирования синтеза топологии БС и БКС наноспутника;

5. Оценка работы алгоритма синтеза топологии БС и БКС;

Объектом исследования является бортовые системы и бортовая кабельная сеть наноспутника.

Предметом исследования является взаимодействие бортовых систем друг с другом

ОБЗОР ЛИТЕРАТУРЫ

В данной работе рассматривается случай сборки бортовых систем наноспутника и синтез топологии бортовой кабельной сети наноспутника исходя из условий обеспечения работоспособности наноспутника.

Для решения поставленных задач в диссертационной работе будут исследованы бортовые системы и бортовая кабельная сеть существующих на производстве наноспутников.Например ниже у нас структурная блок диаграмма бортового компьютера для наноспутника.

Рисунок 2-Блок диаграмма бортового компьютера наноспутника

После изучения ныне существующих бортовых систем и общую сборку наноспутника , будут получены топологические модели БС и БКС. Для этого будут использованы методы теории графов.

Прежде чем определеить понятие графа в наиболее общей форме,полезно рассмотреть геометрическую форму графов. Это позволит с самого начала получить удобное, наглядное представление различных понятий и структур, которые будут рассматриваться в дальнейшем.Любой граф в абстрактном смысле эквивалентен (по отношению к свойствам, изучаемым в теории графов) некоторому геометрическому графу. При некоторой идеализации многие известные структуры можно рассматривать как геометрические графы и изучать с помощью методов теории графов. Например, в виде графа можно представить систему или сеть, в нашем случае это бортовые системы и бортовая кабельная сеть наноспутника....

Геометрический граф есть геометрическая конфигурация или структура в простарнстве, состоящая из множества точек, взаимосвязанных множеством непрерывных, самонепересекающихся кривых.

На рисунке 3 показано оычное представление геометрического графа, с помощью которого можно проиллюстрировать некотороые термины теории графов.

С позиции теории графов элементы ν называются вершинами графа, а соединяющие их неориентированные линии (u) ребрами или дугами, если линии снабжены стрелками, и тогда различают неориентированный граф (рис3.б).Мы будем рассматривать только неориентированные графы.

Для удобства обработки графов с использованием ЭВМ лучше всего подходит матричная форма представления графа. Для неориентированных графов можно определить матрицу смежности вершин (или просто матрицу смежности). Это квадратная матрица S-размера nxn, где строки и столбцы соответсвуют вершинами графа, а элемент 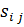равен числу ребер, инцидентных одновременно i-й и j-й вершинами. Таким образом, для графа на рис.4 имеем матрицу смежности

Матрица смежности неориентированного графа (без петель) симметрична относительно главной диагонали, поскольку паре вершин ( 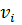, 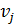) инцидентны одинаковые ребра [ 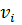, 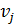]=[ 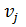, 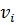], т.е. достаточно рассматривать только половину матрицы выше главной диагонали. Очевидно, что матрица смежности обыкновенного графа (без петель и кратных ребер) является булевой матрицой.

методы математического анализа графов, сетей и алгоритмов, , математические модели реализовались в виде компьютерных программ на языке программирования MatLab и математических расчетов в Excel.

******

В четвёртой главе приведена экспериментальная часть работы, связанная с моделированием и внедрением разработанного метода анализа и синтеза структурной надежности сети передачи данных. Разработанное программное обеспечение реализовано на языке JAVA в среде Eclipse и 14 позволяет проводить анализ структурной надежности сети, а также решать задачи построения оптимальной топологи сети по критериям надежности и стоимости. Приведены результаты работы алгоритмов анализа структурной надежности сети по показателю вероятности связности, позволяющему определить уязвимые места топологии сети, резервирование которых значительно повышает ее структурную надежность. При проведении моделирования использован открытый картографический сервис Mapbox проекта Open Street Map. Показана эффективность применения разработанных эвристических алгоритмов построения оптимальных топологий СПД на примерах, реализованных с помощью сервиса Mapbox.

****

ними отсутствует, а скорость мала по сравнению со скоростью движения КА. При этом для упрощения решения задачи, принято, что КА движется по круговой орбите, а также сопротивлением атмосферы и влиянием других возмущающих сил пренебрегают ввиду их малости по сравнению с силой тяжести Земли. В данной работе учитывается влияние атмосферы и натяжение троса. Также направление движения космонавта и скорость его отделения принято случайными в диапазоне от 0 до 1 м/с. В работе [2] как и в данной работе использовалась линеаризованная модель относительного движения

ЗАКЛЮЧЕНИЕ

Необходимость создания подобных наноспутников-спасателей вытекает из потребности повышения безопасности космонавта при выполнения целого ряда работ в открытом космосе. В данном отчете был проведен обзор существующих методов сближения активных и пассивных космических объектов. Также кратко описано отличие данной работы от существующих.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Р.Ф.Аппазов, О.Г.Сытин, Методы проектирования траекторий носителей и спутников земли// Москва «Наука», 1987, с. 253-257.

2. В.Г.Балахонцев, В.А.Иванов, В.И.Шабанов, Сближение в космосе// М., Воениздат, 1973, 240 с.

3. Ю.П.Яблонько, О сближении космических аппаратов по методу свободных траектории// Фундаментальная и прикладная математика, 2005, том 11, №8 с. 139-147

4. Г.В.Заворуев, Выбор закона управления для синтеза метода наведения на космические объекты при проведении их инспекции// Наука и образование, 2011

5. Military Micro-Sat Explores Space Inspection, Servicing Technologies [электронный ресурс] – режим доступа: http://www.space.com/1336-military-micro-sat-explores-space-inspection-servicing-technologies.html (дата обращения 10.02.17)

6. Е.И.Долженко, Трёхэтапный алгоритм сближения космического аппарата со станцией// УДК 531.352:531.133.1

7. W. H. Clohessy, R. S. Wiltshire. Terminal Guidance System for Satellite Rendezvous // Journal of the Aerospace Sciences. 1960. V.27, N.9. P. 653-658.