Условия прочности. Расчеты на прочность и жесткость
Предельные и допускаемые состояния элементов зданий и сооружений.
Реальные машины и сооружения иногда выходят из строя. Ёстественно, что при перегрузках это случается чаще. В подобных обстоятельствах всегда можно найти тот элемент, который оказался самым 4слабым выход из строя которого послужил причиной отказа в работе всей машины или сооружения. Про вышедший из строя элемент говорят, что он достиг того или иного предельного состояния.
Список предельных состояний весьма обширен. Его открывает, разумеется, предельное состояние разрушения. Однако далеко не всегда достижение предельного состояния связано с разрушением. Например, при случайном падении ручных часов на асфальт может слегка погнуться минутная стрелка, она станет задевать либо за циферблат, либо за стекло. Часы остановятся, т. е. выйдут из строя. Остаточный изгиб стрелки связывают с переходом ее в состояние предельной упругости, когда малый объем этого элемента перешел в состояние пластического течения, а основной объем остался в состоянии упругого деформирования.
Условия прочности. Расчеты на прочность и жесткость.
Нетрудно видеть, что каждому предельному состоянию соответствует свое предельное напряжение, а предельное состояние разрушения обычно возникает тогда, когда нормальное напряжение достигает предела прочности, т. е.
σ=σпред=σult , (2.9.1)
а состояние предельной упругости имеет место в случае, когда в малом объеме конструкционного элемента нормальное напряжение поднимается лишь до предела текучести, т. е.
σ=σпред=σy , (2.9.2)
Эксплуатировать конструкционный элемент при напряжениях, превышающих предельные, нельзя. Нужен некоторый запас на всякого рода случайности. Другими словами, отношение предельного напряжения к расчетному в процессе проектирования изделия:
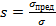 (2.9.3)
(2.9.3)
называемое коэффициентом запаса, должно быть принципиально больше единицы.
Это требование обусловлено несколькими причинами. Укажем на две важнейшие. Во-первых, всякая машина или сооружение проектируется на долговременную нагрузку, которая определяется техническим заданием на новую конструкцию в рамках принятых норм. Такую нагрузку иногда называют номинальной. В упомянутых нормах имеются указания о предельных значениях кратковременных перегрузок в типовых эксплуатационных ситуациях. Однако известно, что в работе отдельных экземпляров машин или сооружений изредка наблюдаются нагрузки, превышающие нормативные. Во-вторых, любой конструкционный материал поставляется на рынок с некоторым разбросом по характеристикам прочности, для каждого материала существуют нормы минимальных значении этих характеристик, ниже которых приемка осуществляться не должна. Однако пробы производятся выборочно, из-за чего за ворота завода изготовителя иногда (хотя и нечасто) уходят партии материала с пониженными характеристиками прочности.
Сказанное можно проиллюстрировать схемой на рис. 2.9.1.
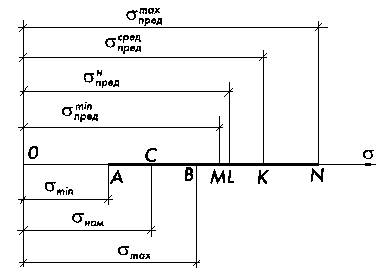
Рисунок 2.9.1
На числовой оси σ отрезок ММ отвечает интервалу случайного разброса характеристики прочности материала σпред (от 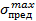 до
до 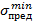 ). Точка К соответствует среднему значению предельного напряжения
). Точка К соответствует среднему значению предельного напряжения 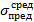 , точка L — нормативному значению
, точка L — нормативному значению 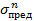 по которому осуществляется указанная выше отбраковка материала. Отрезок АВ указывает на тот интервал напряжения σ в конструкционном элементе, который отвечает случайному рассеиванию внешней нагрузки от минимального до максимального значения. Кроме того на схеме показано так называемое номинальное (нормативное) напряжение σном которое соответствует упомянутой выше долговременной нагрузке. Последняя предполагается действующей на конструкционный элемент в основное время его эксплуатации.
по которому осуществляется указанная выше отбраковка материала. Отрезок АВ указывает на тот интервал напряжения σ в конструкционном элементе, который отвечает случайному рассеиванию внешней нагрузки от минимального до максимального значения. Кроме того на схеме показано так называемое номинальное (нормативное) напряжение σном которое соответствует упомянутой выше долговременной нагрузке. Последняя предполагается действующей на конструкционный элемент в основное время его эксплуатации.
С учетом введенных здесь обозначений уточним понятие коэффициента запаса (2.9.3) следующим образом:
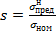 (2.9.4)
(2.9.4)
Схема на рис. 2.9.1 соответствует случаю, когда безопасность эксплуатации обеспечивается наверняка, по тому что:
σmax< 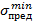 (2.9.5)
(2.9.5)
Посмотрим теперь на эту же ситуацию с экономической точки зрения. Конкурентная борьба на рынках готовой продукции требует снижения материалоемкости изделий, В данном случае такая возможность имеется. В самом деле, некоторое уменьшение площади поперечного сечения стержня при сохранении расчетной длины ведет к уменьшению массы стержня. Если такое сокращение невелико, то неравенство (2.9.5), указывающее на безопасность будущей эксплуатации, остается в силе. Допускаемое сокращение площади сечения определяется равенством:
σmax= 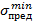 (2.9.5)
(2.9.5)
Другими словами, интервал АВ пододвигается к интервалу МN до совпадения точек В и М. В этом случае вероятность выхода из строя конструкционного элемента все еще равна нулю, а соотношению (2.27) придают вид:
σmax≤ 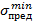 (2.9.5)
(2.9.5)
Основной характеристикой сопротивления материалов силовым воздействиям является нормативное сопротивление Rн, которое устанавливается СНиПом с учетом условий контроля и статистической изменчивости механических свойств материала. В качестве нормативного сопротивления принимают наименьшее контролируемое (браковочное) значение 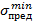 .
.
С середины ХХ века получает все большее распространение еще один подход к расчетам элементов зданий и сооружений на прочность. Речь идет о теории надежности. Здесь считается допустимым, что интервалы АВ и МН по схеме на рис. 2.9.1 частично перекрывают друг друга. В этом случае методами теории вероятностей вычисляют как вероятность выхода элемента из строя, так и вероятность его надежной работы в течение всего срока эксплуатации. Теория надежности возникла из потребности рассчитывать на прочность такие инженерные конструкции, опыта эксплуатации которых у человечества не было. Это ракетные и спутниковые системы, крупные и особо крупные самолеты, атомные и химические реакторы и т. д. Однако по мере накопления опыта эксплуатации машин и сооружений, спроектированных с применением методов теории надежности, начинают складываться нормы допускаемых напряжений.
Возможное отклонение в неблагоприятную сторону от значений нормативного сопротивления учитывается коэффициентом надежности по материалу γм >1. Этот коэффициент отражает статистическую изменчивость свойств материала и их отличие от свойств испытанных образцов. Например, для стали γм=1,025...1,15, для бетона γм=1,3...1,5.
Величина, полученная в результате деления нормативного значения сопротивления на коэффициент надежности по материалу называется расчетным сопротивлением:
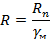
С учетом новых понятий условие безотказной работы конструкционного элемента чаще записывают так
σmax≤ R (2.9.5)
Неравенство (2.9.5) обычно именуют условием прочности, выполнение которого практически гарантирует конструкционный элемент от возникновения предельного состояния в течение всего планового срока эксплуатации.
При расчете по методу предельных состояний формулу 2.9.5 можно записать следующим образом:
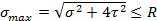 (2.9.6)
(2.9.6)
В строительстве отказываются от понятий допускаемого напряжения и нормативного коэффициента запаса. Условие прочности в этом случае записывают в следующем виде:
N<Nult ; M<Mult (2.9.7)
где N, М — усилие, действующее в рассчитываемом элементе конструкции,
Nult , Mult — предельное усилие, которое может воспринять тот же элемент, если принять во внимание случайное рассеяние характеристики прочности материала.
