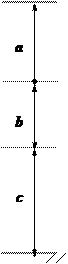КОНТРОЛЬНАЯ РАБОТА № 1. Стальная колонна (Е = 2×104 кН/см2) находится под действием продольной силы Р = 20 кН и
ПРИМЕР К ЗАДАЧЕ 1.1
Стальная колонна (Е = 2×104 кН/см2) находится под действием продольной силы Р = 20 кН и собственного веса ( g = 78 кН/м3).
Требуется:
1. Построить эпюры продольных усилий и нормальных напряжений.
2. Определить опасное сечение и проверить прочность колонны при [s] = 16 кН/ см2.
3. Определить перемещение верхнего среза колонны без учета собственного веса.
 
Рис.1 | Исходные данные: А=10 см2 ; a=2 м; b=1м; с=3м; Р=20 кН. |
РЕШЕНИЕ
Расчетная схема колонны (Рис.2 ) - ступенчатый брус, загруженный заданной сосредоточенной силой Р и распределенной нагрузкой q1, q2, q3 от собственного веса, где
q1 = g А1 = g 2А = 78×20×10-4 = 0.156 кН/м;
q2 = g А2 = g А =78×10×10-4 = 0.078 кН/м;
q3 = g А3 = g 2А =78×20×10-4 = 0.156 кН/м.
R - опорная реакция.
N, кн s, кн/см2
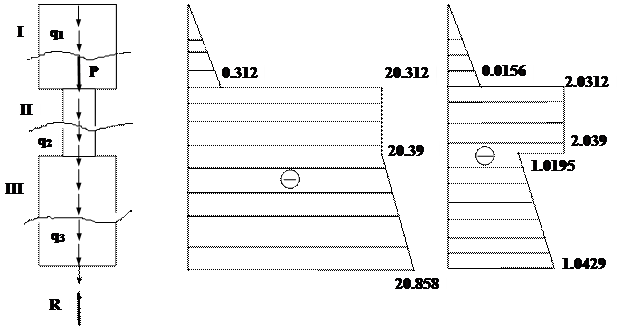 Рис. 2
Рис. 2
Разбиваем стержень на участки, начиная с верхнего свободного конца. Границами участков служат сечения в которых приложены внешние силы или же изменяется площадь поперечного сечения. В данном случае имеем три участка, площади поперечного сечения которых: А1 =2А=20 см2, А2=А=10см2, А3=2А=20см2. Ось z направляем вдоль оси стержня от верхнего среза колонны. Для каждого участка находим внутренние продольные силы NZ методом сечений из условия равновесия отсеченной верхней части (при этом отпадает необходимость в определении реакции заделки R). Нормальные напряжения sz.= 
1-ый участок 0 £ z1 £ a


 0 £ z1 £ 2
0 £ z1 £ 2


 q1 z1
q1 z1 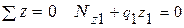
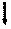 Nz1
Nz1 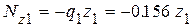
z 

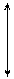


 2 -ой участок a £ z 2 £ a+b
2 -ой участок a £ z 2 £ a+b
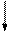 2 £ z2 £ 3
2 £ z2 £ 3
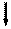 a q1 z2
a q1 z2 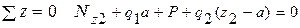
 P
P 

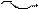
 q2
q2 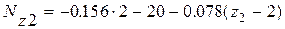
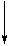 Nz2
Nz2 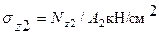
z


 3 -ий участок a+ b £ z3 £ a+b+c
3 -ий участок a+ b £ z3 £ a+b+c
 3 £ z 3 £ 6
3 £ z 3 £ 6
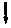 a q1
a q1 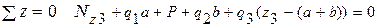


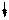
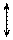 P z3
P z3 


 b q2
b q2 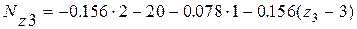


 q3
q3 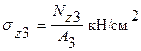
 Nz3
Nz3
z
Зависимости NZ и sZ линейно зависят от z. Для построения эпюр достаточно вычислить их значения на границах участков. Эпюры NZ и sZ строим рядом с расчетной схемой (рис. 2). Ось абсцисс графиков проводим параллельно оси бруса. По оси ординат откладываем в выбранном масштабе значение продольной силы NZ или нормального напряжения sZ соответственно. Указываем знак. Штриховка должна быть перпендикулярна оси.
2. По эпюре нормальных напряжений sZ определяем опасное сечение. Опасное сечение - сечение в котором 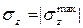 .
. 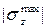 = 2.039 кН/см2. В опасном сечении записываем условие прочности при растяжении-сжатии:
= 2.039 кН/см2. В опасном сечении записываем условие прочности при растяжении-сжатии:
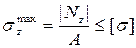 ,
, 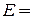
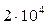 кН/см2
кН/см2
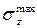 =2.039 кН/см2 < 16 кН/см2 . Условие прочности выполняется.
=2.039 кН/см2 < 16 кН/см2 . Условие прочности выполняется.
3. Результаты расчета показывают, что собственный вес колонны мал по сравнению с приложенной нагрузкой Р. Поэтому при определении перемещения Dl верхнего среза стальной колонны собственный вес не учитываем. По закону Гука для растяжения-сжатия:
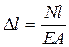
Определяем D l как сумму удлинений ( укорочений ) отдельных участков.
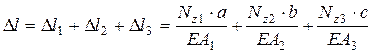
Без учета собственного веса (q1 = 0, q2 = 0, q3 = 0)
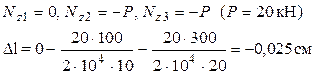
Отрицательное значение Dl показывает, что колонна укоротилась.
ПРИМЕР К ЗадаЧЕ 1.2
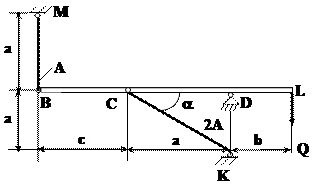
Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стальным стержням при помощи шарниров.
Требуется:
1. Найти усилия и напряжения в стержнях, выразив их через силу Q.
2. Используя метод расчета по допускаемым напряжениям найти допускаемую нагрузку [Q].
3. Найти предельную грузоподъемность системы Qт и допускаемую нагрузку [Q]т путем расчета по предельному состоянию. Запас прочности к = 1.5.
4. Сравнить величины [Q] и [Q]т .
Рис.1 | a = 40 см, b = 20 см, с= 30 см А - площадь поперечного сечения стержня ВМ 2А- площадь поперечного сечения стержня СК А = 10 см2 , sт = 24 кН/см2 [s] = 16 кН/см2 |
РЕШЕНИЕ
1. Определяем необходимые геометрические параметры (длины стержней ВМ и СК, a - угол наклона стержня СК).
l1=ВМ=40 см
l2=СК= 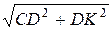 =
= 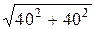 = 56.569 см
= 56.569 см
sin a = DК / СК = 40 / 56.569= 0.707, cos a = СD/CK=0,707
2. Строим силовую схему (рис. 2). Указываем направление опорных реакций RD и HD, внутренних усилий в стержнях N1 и N2. Неизвестные усилия N1 и N2 считаем растягивающими.
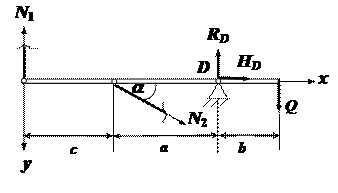
Рис.2
3. Определяем степень статической неопределимости m = 4 - 3 = 1
Здесь 4 - число неизвестных ( RD, HD, N1, N2)
3 - число уравнений статики.
4. Записываем уравнения статики
S x = 0 HD + N2 cosa = 0;
S y = 0- N1 - RD + N2 sina + Q= 0 ;
S MD= 0 - N1 70 + N2 40 sin a - Q20 = 0.
В данной задаче не требуется отыскивать опорные реакции RD и HD, поэтому из трех уравнений статики используем одно:
S MD= 0 - N1 70 + N2 40 sin a - Q 20 = 0 (1)
Из одного уравнения (1) невозможно определить два неизвестных усилия N1 и N2.
Задача один раз статически неопределима.
5. Составляем условие совместности деформаций.
Используя предположение о малости деформаций, строим деформированную схему конструкции (рис. 3). Абсолютно жесткий брус BL под действием приложенной нагрузки Q поворачивается на малый угол вокруг опоры (т.D), оставаясь прямолинейным. При этом первый стержень сжимается на величину Dl1 ( т. В переходит в т. В1 ), а второй стержень растягивается на величину Dl2 (т.С переходит в С1 ).
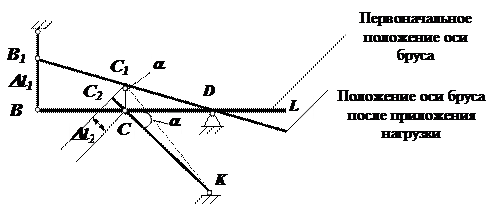
Рис. 3
Здесь ВВ1 ^ BD, CC1 ^ CD, D l1 = BB1, D l2 = CC2
Чтобы получить т. С2 из т. С1 опускаем перпендикуляр на первоначальное направление стержня СК.
Из подобия треугольников D BB1D и D СС1D следует:
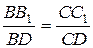 или
или 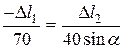
Здесь CC1 = Dl2 / sin a из D CC1C2. Знак минус показывает, что первый стержень укорачивается. Итак получили условие совместности деформаций:
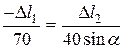 или
или  (2)
(2)
6. Используя закон Гука, из уравнений (1) и (2) определяем усилие и напряжения. Согласно закону Гука:
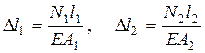
По условию задачи А2 = 2 А1
Подставляя в (2), получим N1= -1,750 N2 (3)
Решаем совместно систему уравнений (1), (3). Получаем:
- (-1.750 N2 ) 70 + N2 40 0.707 - Q 20 =0. Откуда
N2 = 0,133 Q ( растяжение )
N1 = - 1,750 N2 = - 0.233 Q ( сжатие )
Определяем напряжения в стержнях:
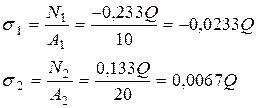
где A1 =A =10 см2 A2 = 2 A = 20 см2
7. Определяем допускаемую нагрузку [Q].
Приравнивая максимальное напряжение по модулю |s1| допускаемому [s], получаем допускаемую нагрузку [Q]:
|s1 | = 0.0233 [Q] = 16 кН/см2 Þ [Q] = 16 / 0.0233 = 689.655 кН.
8. Вычисляем предельную грузоподъемность QТ.
Считаем s1 = sT, s2 =sT. Тогда 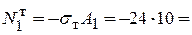 240 кН, (сжатие)
240 кН, (сжатие)
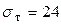 кН/см2,
кН/см2, 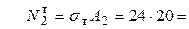 480 кН.
480 кН.
Подставляя 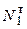 и
и 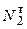 в (1), с учетом истинного направления усилия
в (1), с учетом истинного направления усилия 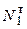 (сжатия), находим предельное значение QТ:
(сжатия), находим предельное значение QТ:
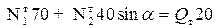
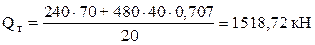
Допускаемое значение [Q]т по предельному состоянию
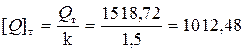 кН
кН
9. Сравнивая величины [Q] = 689,655 кН и [Q]T =1012.48 кН, видим, что расчет по предельному состоянию позволяет расширить диапазон допускаемых нагрузок
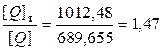 .
.
ПРИМЕР К ЗАДАЧЕ 1.3.
Круглый стальной вал сплошного сечения жестко закрепленный одним концом, находится под действием четырех внешних скручивающих моментов M1=3,5 кН×м, М2=5 кН×м, М3=4 кН×м, М4=2,5 кН×м (рис.1).
Требуется :
1. Построить эпюру крутящих моментов.
2. Определить диаметр вала из расчета на прочность [t]=6 кН/см2.
3. Построить эпюру углов закручивания G = 8´103 кН/см2
4. Найти наибольший относительный угол закручивания на 1 м длины.
*Примечание:На рис.1.3 использовано плоское изображение крутящих моментов:
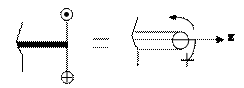
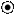 - означает начало стрелки (“на нас”); - конец стрелки (“от нас”).
- означает начало стрелки (“на нас”); - конец стрелки (“от нас”).
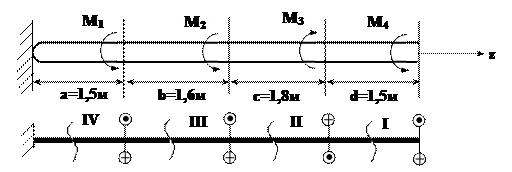
Рис. 1
РЕШЕНИЕ
1. Построение эпюры крутящих моментов.
Для определения крутящего момента в сечении пользуемся методом сечений. Разбиваем вал на участки, начиная со свободного конца. Границами участков служат точки приложения внешних крутящих моментов.
Для данного вала получаем 4 участка. Для каждого из участков рассматриваем равновесие отсеченной правой части. Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, действующих по одну сторону от сечения. Для правой отсеченной части Мz направлен по часовой стрелке, если смотреть с положительного направления оси z.
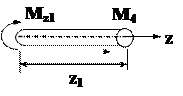
1 участок: 0 £ z1 £ 1,5 м
| åMZ = 0 -MZ1 + M4=0 MZ1 = M4 = 2,5 кН×м |
2 участок: 1,5 £ z2 £ 3,3 м
| åMZ = 0 -MZ2 -М3 + M4=0 MZ2 = M4 - M 3 = 2,5 -4 = -1,5 кН×м |
3 участок: 3,3 £ z3 £ 4,9 м
| åMZ = 0 -MZ3+М2 –М3 + M4=0 MZ3 = M4 - M 3 + М2 = = 2,5 -4 + 5 = 3,5 кН×м |
4 участок: 4,9 £ z4 £ 6,4 м
åMZ = 0 -MZ4 + M1 + M2 - M3 + M4 = 0
MZ4 = M4 - M3 + М2 + М1 = 2,5 - 4 + 5 + 3,5 = 7 кН×м
Эпюры крутящих моментов показаны на рис.2
Опасное сечение - сечение в котором крутящий момент принимает максимальное значение МZmax =7 кН×м - все точки 4 -го участка.
2. Подбор диаметра вала
По наибольшему моменту MZmax из условия прочности при кручении подбираем диаметр вала:
tmax = 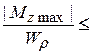 [t]
[t]
Полярный момент сопротивления для круглого сечения 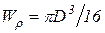 ;
;
MZmax = 7 кН×м =700 кН×см.
Отсюда
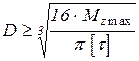 =
= 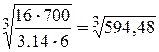 = 8.4 см = 84 мм.
= 8.4 см = 84 мм.
После округления до стандартного значения получаем D = 90 мм=0.09 м.
3. Вычисляем углы закручивания j.
Обозначаем буквами А, В, С, D, Е границы участков, начиная с заделки (рис.2). Если на участке вала длины l крутящий момент M и жесткость GIр постоянны, то угол поворота торцевых сечений определяется по формуле:
j = 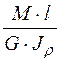
G = 8 × 103 кН/см2 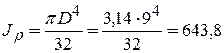 см4
см4
Жесткость вала при кручении GIr = 8 ×103 × 643,8 = 5,15 106 кН см2
Вычисляем углы закручивания начиная от неподвижного сечения. В заделке jА = 0
jВ = jА + jАВ =0+ 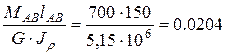 (рад)
(рад)
Здесь jAB угол поворота торцевых сечений на участке AB. MAB = MZ4 = 7 кН×м = 700 кН×см, lAB= 1.5м = 150 см (длина участка AB )
Аналогично получаем:
jC = jB + jBC =jВ+ 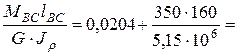 0.0204+0.0109=0.0313 (рад);
0.0204+0.0109=0.0313 (рад);
jD = jc + jCD =jc+ 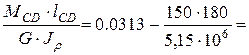 0.0313-0.052=0.0261 (рад);
0.0313-0.052=0.0261 (рад);
jЕ = jD + jDE =jD+ 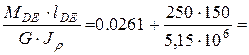 0.0261+0.0073=0.034 (рад).
0.0261+0.0073=0.034 (рад).
Эпюры углов поворота приведены на рис.2.
4. Вычисляем относительные углы закручивания на каждом участке.
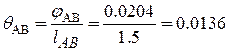 (м-1);
(м-1);
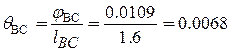 (м-1);
(м-1);
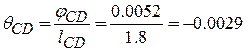 (м-1);
(м-1);
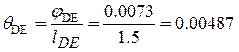 (м-1).
(м-1).
Наибольший угол закручивания на 1 метр длины qmax = qAB =0.0136 (м-1 ).
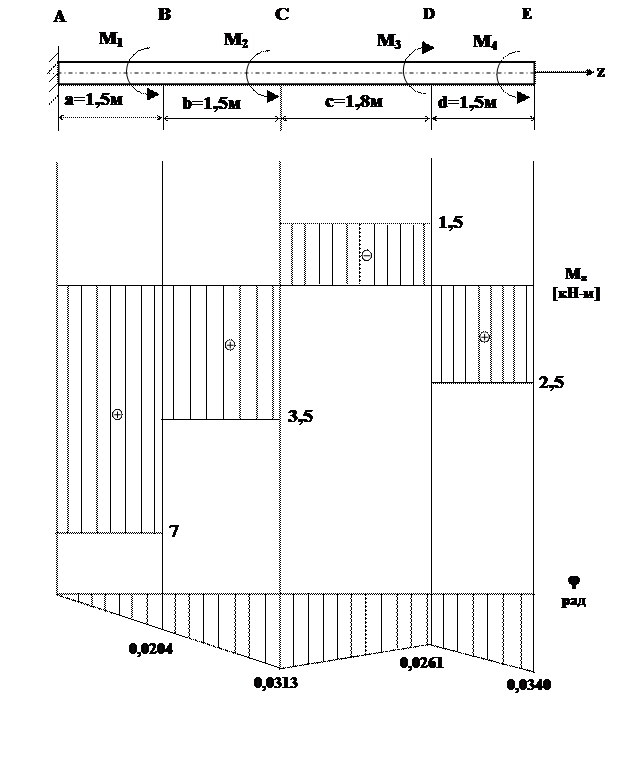
Рис. 2.