Управляющий автомат мили

Автомат с жёсткой логикой

Теория управляющих абстрактных и конечных автоматов – очень обширная наука, описывающая понятие автоматов, их поведение, формализацию, различные модели и пр. Здесь не будут рассматриваться все эти теоретические аспекты, рассмотрим лишь две практических варианта УА с жёсткой логикой. Название «автомат с жёсткой логикой» проистекает из того, что алгоритм функционирования такого автомата жёстко задан его схемой. Для внесения даже незначительных изменений в алгоритм необходимо полностью (или почти полностью) пересинтезировать всю схему автомата. «Отделаться» какими-то мелкими изменениями возможно далеко не всегда.

Обобщённая структурная схема УА с жёсткой логикой имеет вид – рис. 2.

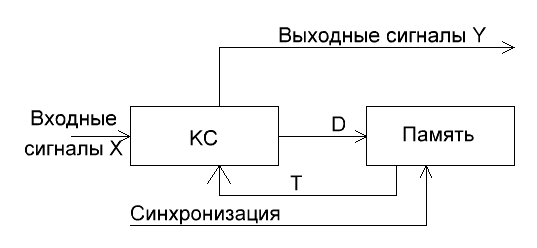
Рис. 2. Обобщённая структурная схема УА с жёсткой логикой

На рис. 2: X – множество входных сигналов автомата, Y – множество выходных сигналов, D – сигналы управления памятью, T – сигналы состояния. УА состоит из 2-х функциональных блоков:

1. КС – комбинационная схема, формирующая выходные сигналы автомата и сигналы управления памятью.

2. Память автомата – просто набор триггеров (регистр). Кол-во триггеров n определяется кол-вом k требуемых состояний автомата. k определяется по-разному для разных автоматов. k равно ближайшему целому (в большую сторону) числу из значений выражения 2ⁿ. Т.е. n=]log₂k[. Например, если у нас 5 состояний, то мы должны поставить 3 триггера (2³=8>5), а если 8, то 4 (2⁴=16>8).

Функционирование УА может задаваться графом переходов либо таблицами истинности. Можно описать его поведение и формулами: Y=ƒ1(X,T), D=ƒ2(X,T).

Очевидно, что при использовании одновходовых триггеров (D и Т) КС получается проще (для каждого триггера формировать надо только один сигнал вместо 2, как для RS или JK триггеров). На практике, если, например, в наличии есть только RS-триггеры, то можно несколько «схитрить», сделав D-триггеры из RS и синтезировать КС в расчёте на D.

Следует также отметить, что всегда следует применять триггеры с синхронизацией. Если использовать триггеры без синхронизации, например, асинхронные RS-триггеры, то полученный автомат будет «перещёлкивать» все свои состояния очень быстро, со скоростью, определяемой скоростью работы элементов, входящих в КС и самих триггеров. Кроме того, на выходе могут появляться какие-то другие, случайные и «незапланированные» комбинации состояний выходов.

Если применяются D-триггеры, то можно использовать обычные регистры хранения вместо раздельных триггеров. Это может существенно упростить конечную схему.

УА с жёсткой логикой бывают 2-х видов – Мили и Мура.

Управляющий автомат Мили

Автомат Мили имеет структуру, на 100% совпадающую с рис. 2. И поведение его описывается теми же общими формулами – Y=ƒ1(X,T), D=ƒ2(X,T). Поэтому иногда говорят, что этот автомат генерирует (в смысле изменяет) выходные сигналы при переходах из одного состояния в другое. Здесь подчёркивается тот факт, что Y непосредственно зависит от X.

Рассмотрим синтез автомата Мили на примере.

Допустим, нам необходимо построить автомат, имеющий 2 входных сигнала (x1, x2) и 4 выходных (y1-y4):

x1	x2	y1	y2	y3	y4

Т.к. мы имеем 6 состояний, то нам понадобится 3 триггера. Используем для простоты D-триггеры. Построим теперь полную таблицу истинности автомата:

Сост.

T1

T2

T3

x1

x2

y1

y2

y3

y4

D1

D2

D3

Здесь мы:

1. Пронумеровали все состояния автомата.
2. Закодировали все 6 состояний автомата сигналами текущего состояния триггеров Tx. Кодировать можно как угодно, единственное требование – все коды состояний д.б. уникальны. Т.е. не должно быть 2-х и более состояний с одинаковыми кодами.
3. Дополнили исходную таблицу сигналами Tx и сигналами Dx управления триггерами для того, чтобы автомат мог переходить из одного состояния в другое.

Также подразумевается, что состояния меняются по кругу. В разделе 1.2 показано, как реализовывается переход их одного состояния в 2 других в зависимости от разных входных сигналов.

По этой таблице уже можно синтезировать КС автомата. Но перед тем, как перейти непосредственно к синтезу, отметим небольшую особенность использованного кодирования состояний: сигнал T1 повторяет x1 со сдвигом на один такт. Это позволяет не строить какие-то формулы и схемы для сигнала D1, а сразу пустить x1 на D1. Подобные «уловки» в ряде случаев позволяют упростить схему и ускорить её быстродействие.

КС должна формировать 7 сигналов: y1-y4 и D1-D3. Составим формулы для каждого сигнала:

По формулам можно нарисовать схему автомата. Мы этого делать не будем, здесь и так всё понятно.

Следует отметить, что у автомата Мили теоретически возможна ситуация, при которой окажется, что какой-то yi зависит только от xj и не зависит от Tn. Т.е. автомат изменяет выходные сигналы, не изменяя своего состояния. Учесть это при синтезе сложно, гораздо проще после него ввести какие-то «ненужные» зависимости yi от каких-то Tn.