Уровень 3: уровень операционной системы

Этот уровень обычно является гибридным. Большинство команд в его языке есть также и на уровне архитектуры набора команд (команды, имеющиеся на одном из уровней, вполне могут быть представлены и на других уровнях). У этого уровня есть некоторые дополнительные особенности: новый набор команд, другая организация памяти, способность выполнять две и более программы одновременно и некоторые другие. При построении уровня 3 возможно больше вариантов, чем при построении уровней 1 и 2.

Новые средства, появившиеся на уровне 3, выполняются интерпретатором, который работает на втором уровне. Этот интерпретатор был когда-то назван операционной системой. Команды уровня 3, идентичные командам уровня 2, выполняются микропрограммой или аппаратным обеспечением, но не операционной системой. Другими словами, одна часть команд уровня 3 интерпретируется операционной системой, а другая часть — микропрограммой. Вот почему этот уровень считается гибридным. Мы будем называть этот уровень уровнем операционной системы.

Между уровнями уровнем архитектуры набора команд и уровнем операционной системы есть существенная разница. Нижние три уровня задуманы не для того, чтобы с ними работал обычный программист. Они изначально ориентированы на интерпретаторы и трансляторы, поддерживающие более высокие уровни. Эти трансляторы и интерпретаторы составляются так называемыми системными программистами, которые специализируются на разработке новых виртуальных машин. Уровни с четвертого и выше предназначены для прикладных программистов, решающих конкретные задачи.

Еще одно изменение, появившееся на уровне операционной системы, — механизм поддержки более высоких уровней. Уровни 2 и 3 обычно интерпретируются, а уровни 4, 5 и выше обычно, хотя и не всегда, транслируются.

Другое отличие между уровнями 1, 2, 3 и уровнями 4, 5 и выше — особенность языка. Машинные языки уровней 1, 2 и 3 — цифровые. Программы, написанные на этих языках, состоят из длинных рядов цифр, которые воспринимаются компьютерами, но малопонятны для людей. Начиная с уровня 4, языки содержат слова и сокращения, понятные человеку.

Уровень 4: уровень Ассемблера

Уровень 4 представляет собой символическую форму одного из языков более низкого уровня. На этом уровне можно писать программы в приемлемой для человека форме. Эти программы сначала транслируются на язык уровня 1, 2 или 3, а затем интерпретируются соответствующей виртуальной или фактически существующей машиной. Программа, которая выполняет трансляцию, называется ассемблером.

Уровень 5: уровень языка прикладных программистов

Уровень 5 обычно состоит из языков, разработанных для прикладных программистов. Такие языки называются языками высокого уровня. Существуют сотни языков высокого уровня. Наиболее известные среди них — С, C++, Java, LISP и Prolog. Программы, написанные на этих языках, обычно транслируются на уровень 3 или 4. Трансляторы, которые обрабатывают эти программы, называются компиляторами. Отметим, что иногда также имеет место интерпретация. Например, программы на языке Java сначала транслируются на язык, напоминающий ISA и называемый байт-кодом Java, который затем интерпретируется.

В некоторых случаях уровень 5 состоит из интерпретатора для конкретной прикладной области, например символической логики. Он предусматривает данные и операции для решения задач в этой области, выраженные при помощи специальной терминологии.

Итог

Таким образом, компьютер проектируется как иерархическая структура уровней, которые надстраиваются друг над другом. Каждый уровень представляет собой определенную абстракцию различных объектов и операций. Рассматривая компьютер подобным образом, мы можем не принимать во внимание ненужные нам детали и, таким образом, сделать сложный предмет более простым для понимания.

Набор типов данных, операций и характеристик каждого отдельно взятого уровня называется архитектурой. Архитектура связана с программными аспектами. Например, сведения о том, сколько памяти можно использовать при написании программы, — часть архитектуры. Аспекты реализации (например, технология, применяемая при реализации памяти) не являются частью архитектуры. Изучая методы проектирования программных элементов компьютерной системы, мы изучаем компьютерную архитектуру. На практике термины «компьютерная архитектура» и «компьютерная организация» употребляются как синонимы.

2 !Вентили и булева алгебра (транзисторные схемы, значки, таблицы истинности…)

Основные элементы, из которых конструируются цифровые компьютеры, чрезвычайно просты. При конструировании этих элементов используется специальная двузначная алгебр (булева алгебра).

Вентили

Цифровая схема — это схема, в которой есть только два логических значения. Обычно сигнал от 0 до 1 В представляет одно значение (например, 0), а сигнал от 2 до 5 В — другое значение (например, 1). Напряжение за пределами указанных величин недопустимо. Крошечные электронные устройства, которые называются вентилями, позволяют получать различные функции от этих двузначных сигналов. Вентили лежат в основе аппаратного обеспечения, на котором строятся все цифровые компьютеры. Вся современная цифровая логика основывается на том, что транзистор может работать как очень быстрый бинарный переключатель.

Рисунок 1 – Транзистрорный инвертор

Транзистор имеет три соединения с внешним миром: коллектор, базу и эмиттер. Если входное напряжение Vin ниже определенного критического значения, транзистор выключается и действует как очень большое сопротивление. Это приводит к выходному сигналу Vout, близкому к Vcc (напряжению, подаваемому извне), — для данного типа транзистора это обычно +5 В. Если Vin превышает критическое значение, транзистор включается и действует как проводник, вызывая заземление сигнала Vout (по соглашению — это 0 В). Важно отметить, что если напряжение Vin низкое, то Vout высокое, и наоборот. Эта схема, таким образом, является инвертором, превращающим логический 0 в логическую 1 и логическую 1 в логический 0. Резистор (ломаная линия) нужен для ограничения тока, проходящего через транзистор, чтобы транзистор не сгорел. На переключение из одного состояния в другое обычно требуется несколько наносекунд.

Рисунок – Вентиль НЕ И

На рисунке два транзистора соединены последовательно. Если и напряжение V1 и напряжение V2 высокое, то оба транзистора становятся проводниками и снижают Vout. Если одно из входных напряжений низкое, то соответствующий транзистор выключается и напряжение на выходе становится высоким. То есть, напряжение Vout является низким тогда и только тогда, когда и напряжение V1 и напряжение V2 высокое.

Рисунок 3 – Вентиль НЕ ИЛИ

На рисунке два транзистора соединены параллельно. Если один из входных сигналов высокий, включается соответствующий транзистор и снижает выходной сигнал. Если оба напряжения на входе низкие, то выходное напряжение становится высоким.

Данные три схемы образуют три простейших вентиля: НЕ, НЕ-И и НЕ-ИЛИ соответственно. Вентили НЕ часто называют инверторами.

Определим высокое напряжение (Vcc) как логическую 1, а низкое напряжение («земля») — логический 0. Тогда можно выражать значение на выходе как функцию от входных значений. Значки, которые используются для изображения этих трех типов вентилей, показаны на рисунке. Там же показаны режимы работы функции для каждой схемы. На этих рисунках А и В — входные сигналы, X — выходной сигнал. Каждая строка таблицы определяет выходной сигнал для различных комбинаций входных сигналов.

Рисунок 4 – Вентили НЕ, НЕ-И, НЕ-ИЛИ

Если выходной сигнал вентиля НЕ-И подать в инвертор, то можно получить другую схему, противоположную вентилю НЕ-И, у которой выходной сигнал равен 1 тогда и только тогда, когда оба входных сигнала равны 1. Такая схема называется вентилем И. Ее изображение и описание соответствующей функции даны на рисунке:

Рисунок – Вентиль И

Точно так же вентиль НЕ-ИЛИ может быть связан с инвертором. Тогда получится схема, у которой выходной сигнал равен 1 в том случае, если хотя бы один из входных сигналов единичный, и равен 0, если оба входных сигнала нулевые. Изображение этой схемы, которая называется вентилем ИЛИ, а также описание соответствующей функции даны на рисунке.

Рисунок – Вентиль ИЛИ

Маленькие кружочки в схемах инвертора, вентиля НЕ-И и вентиля НЕ-ИЛИ называются инвертирующими выходами. Они также могут использоваться в другом контексте для указания на инвертированный сигнал.

Пять представленных вентилей составляют основу цифрового логического уровня. Для построения вентилей НЕ-И и НЕ-ИЛИ требуются по два транзистора, а для вентилей И и ИЛИ — по три транзистора на каждый вентиль. По этой причине во многих компьютерах используются вентилиНЕ-И и НЕ-ИЛИ, а не И и ИЛИ.

Две основные технологии производства вентилей:

· -биполярная;

· -МОП (металл, оксид, полупроводник).

Среди биполярных технологий можно выделить:

· -ТТЛ (транзисторно-транзисторная логика), которая служила основой цифровой электроники на протяжении многих лет,

· -ЭСЛ (эмиттерно-связанная логика), которая используется в тех случаях, когда требуется высокая скорость выполнения операций.

В отношении вычислительных схем более распространена технология МОП. МОП-вентили работают медленнее, чем ТТЛ и ЭСЛ, но потребляют гораздо меньше энергии и занимают гораздо меньше места, поэтому можно компактно расположить большое количество таких вентилей. Вентили МОП имеют несколько разновидностей: р-канальный МОП, n-канальный МОП и комплементарный МОП. Современные процессоры и память чаще всего производятся с использованием технологии комплементарных МОП, которая работает при напряжении +3,3 В.

Булева алгебра

Чтобы описать схемы, получаемые сочетанием различных вентилей, нужен особый тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1. Такая алгебра называется булевой (названа в честь английского математика Джорджа Буля 1815-1864).

В булевой алгебре есть свои функции. Булева функция на входе получает одну или несколько переменных и выдает результат, который зависит только от значений этих переменных. Можно определить простую функцию f, сказав, что f(A) = 1, если А = 0, и f(А) = 0, если А = 1. Такая функция будет функцией НЕ. Так как булева функция от п переменных имеет только 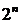возможных комбинаций значений переменных, то такую функцию можно полностью описать в таблице с 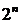строками. В каждой строке будет даваться значение функции для разных комбинаций значений переменных. Такая таблица называется таблицей истинности.

Строки таблицы истинности располагаются по порядку номеров, то есть для двух переменных в порядке 00, 01, 10, 11. Булеву функцию можно полностью описать 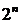-разрядным двоичным числом, которое получается, если считывать по вертикали колонку результатов в таблице истинности. Таким образом, НЕ-И - это 1110, НЕ-ИЛИ - 1000, И - 0001 и ИЛИ - 0111.

Существуют только 16 булевых функций от двух переменных, которым соответствуют 16 возможных 4-разрядных цепочек.

На рисунке показана таблица истинности для булевой функции от трех переменных: М = f(A, B,C). Это функция большинства, которая принимает значение 0, если большинство переменных равны 0, или 1, если большинство переменных равны 1.

Рисунок – Схема реализации функции большинства

Таблица истинности для функции большинства

С возрастанием количества переменных описание булевой функции с помощью таблицы истинности становится громоздким. Поэтому вместо таблиц истинности часто используется другой вариант записи.

Любую булеву функцию можно определить, указав, какие комбинации значений входных переменных приводят к единичному значению функции. Для функции большинства существует 4 комбинации переменных, которые дают единичное значение функции. Для того, чтобы показать что значение переменной инвертируется, над переменной ставят черту. Отсутствие черты означает, что значение переменной не инвертируется.

Для обозначения булевой функции И используется знак умножения (точка, ·).

Для обозначения булевой функции ИЛИ используется знак сложения (+). Например, принимает значение 1, только если A = 1, B = 0 и С = 1. Кроме того, принимает значение 1, только если (А = 1 и В = 0) или (В = 1 и С = 0). В таблице истинности функция принимает значение 1 в четырех строках: . Функция М принимает значение истины (то есть 1), если одно из этих четырех условий истинно. Следовательно:

.

Это компактная запись таблицы истинности. Таким образом, функцию от n переменных можно описать суммой максимум 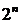произведений, при этом в каждом произведении будет по n множителей. Булева функция может быть реализована электронной схемой (часто различными способами) с использованием сигналов, которые представляют входные и выходные переменные, и вентилей, например, И, ИЛИ и НЕ.