Создание модифицированных сетей Хопфилда

Сеть Хопфилда создается функцией newhop. Алгоритм синтеза сети реализован в функции solvehop2, являющейся подфункцией функции newhop (описание функции solvehop2 см. в [1]).

Если задано множество целевых точек равновесия, представленных матрицей Т, то функция newhop возвращает матрицу весов и вектор смещений для рекуррентного слоя сети Хопфилда. При этом гарантируется, что точки устойчивого равновесия будут соот­ветствовать целевым векторам, но могут появиться и так называемые паразитные точки. В процессе синтеза сети число таких нежелательных точек сводится к минимуму.

Когда сеть спроектирована, она может быть проверена с одним или большим числом векторов входа. Весьма вероятно, что векторы входа, близкие к целевым точкам, равнове­сия найдут свои цели. Способность модифицированной сети Хопфилда быстро обрабаты­вать наборы векторов входа позволяет проверить сеть за относительно короткое время. Сначала можно проверить, что точки равновесия целевых векторов действительно при­надлежат вершинам гиперкуба, а затем можно определить области притяжения этих точек и обнаружить паразитные точки равновесия, если они имеются.

Рассмотрим следующий пример [2]. Предположим, что требуется создать модифицирован­ную сеть Хопфилда с двумя точками равновесия, заданными в трехмерном пространстве:

>> T=[-1 -1 1; 1 -1 1]'

T =

-1 1

-1 -1

1 1

Выполним синтез сети, используя М-функцию newhop:

>> net = newhop(T);

Проверим, что разработанная сеть имеет устойчивые состояния в этих двух точках. Выполним моделирование сети Хопфилда, приняв во внимание, что эта сеть не имеет входов и содержит рекуррентный слой; в этом случае целевые векторы определяют начальное состоя­ние слоя Ai, а второй аргумент функции net представляет собой пустой массив ячеек, первый аргумент задает шаг дискретности и число временных шагов (тактов) — используем два шага. Функция возвращает массив ячеек Y, соответствующих каждому временному шагу

>> Ai = {T};

>> [Y,Pf,Af] = net(cell(1,2),{},Ai);

>> Y{2,2}

ans =

-1 1

-1 -1

1 1

Выходными аргументами функции net являются массив ячеек выходов сети Y, состояния на линиях задержки входов после моделирования Pf, состояния на линиях задержки слоев после моделирования Af. Аргументы Pf и Af можно опустить. Действительно, устойчивые положения равновесия сети находятся в назначенных точках.

Зададим другое начальное условие в виде массива ячеек:

>> Ai = {[-0.9; -0.8; 0.7]};

Эта точка расположена вблизи первого положения равновесия, так что можно ожидать, что сеть будет сходиться именно к этой точке. Чтобы убедиться, что это произойдет, промоделируем работу сети на 5 шагах:

>> [Y,Pf,Af] = net(cell(1, 5),{},Ai);

>> Y{1,1}

ans =

-1

-1

Сеть из заданного начального состояния вернулась в устойчивое по­ложение равновесия. Желательно, чтобы сеть вела себя аналогичным образом при зада­нии любой начальной точки в пределах куба, вершины которого составлены изо всех комбинаций чисел 1 и -1 в трехмерном пространстве. К сожалению, этого нельзя гаранти­ровать, и достаточно часто сети Хопфилда включают нежелательные паразитные точки равновесия.

Рассмотрим сеть Хопфилда с четырьмя нейронами (программа Hopfield.m):

% Программа моделирования модифицированной сети Хопфилда

clear % очистка рабочего пространства

clc % очистка командного окна

close all % Закрытие всех окон

T=[1 -1; -1 1; 1 1; -1 -1]'

% точки равновесия

plot(T(1, :), T(2, :), '*r');

axis([-1.1 1.1 -1.1 1.1]);

title('Точки равновесия сети Хопфилда');

xlabel('a(1)'), ylabel('a(2)');

grid on;

disp('Нажмите Enter')

pause

% Создание сети

net=newhop(T);

% Проверка принадлежности вершин квадрата к сети Хопфилда

Ai = {T};

Y = net(cell(1,2),{},Ai);

disp('Проверка принадлежности вершин квадрата к сети Хопфилда');

Y{1,1}

% Поведение сети при случайных начальных условиях

plot(T(1, :),T(2, :), 'r*');

hold on;

axis([-1.5 1.5 -1.5 1.5]);

xlabel('a(1)'), ylabel('a(2)');

for i=1:25

a={[-1.5; -1.5]+3*rand(2,1)}; % случайный вектор

Y=net(cell(1,50), {}, a); %модел. при случ. нач. условиях

% Y - массив ячеек, соответствующих каждому шагу моделирования

record=[cell2mat(a) cell2mat(Y)];

start=cell2mat(a);

plot(start(1,1), start(2, 1), 'kx', record(1, :), record(2, :));

end

grid on

title('Поведение сети при случайных начальных условиях');

Сначала определим 4 точки равновесия в виде следующего массива целевых векторов

T =

1 -1 1 -1

-1 1 1 -1

Следующий фрагмент программы строит эти 4 точки равновесия на плоскости состояний сети Хопфилда (рис. 5.3):

plot(T(1, :), T(2, :), '*r');

axis([-1.1 1.1 -1.1 1.1]);

title('Точки равновесия сети Хопфилда');

xlabel('a(1)'), ylabel('a(2)');

grid on;

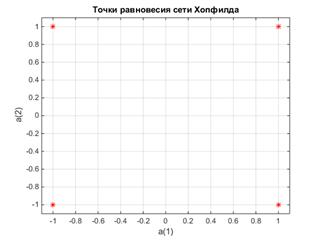
Рис.54.3. Точки равновесия сети Хопфилда

Далее создается сеть Хопфилда

net=newhop(T);

И проверяется, принадлежат ли вершины квадрата к сети Хопфилда

Ai = {T};

Y = net(cell(1,2),{},Ai);

disp('Проверка принадлежности вершин квадрата к сети Хопфилда');

Y{1,1}

Как и следовало ожидать, выходы сети равны целевым векторам.

Далее проверяется поведение сета при случайных начальных условиях:

plot(T(1, :),T(2, :), 'r*');

hold on;

axis([-1.5 1.5 -1.5 1.5]);

xlabel('a(1)'), ylabel('a(2)');

for i=1:25

a={[-1.5; -1.5]+3*rand(2,1)}; % случайный вектор

Y=net(cell(1,50), {}, a); %модел. при случ. нач. условиях

% Y - массив ячеек, соответствующих каждому шагу моделирования

record=[cell2mat(a) cell2mat(Y)];

start=cell2mat(a);

plot(start(1,1), start(2, 1), 'kx', record(1, :), record(2, :));

end

grid on

title('Поведение сети при случайных начальных условиях');

Для проверки 25 раз формируются ячейки, содержащие случайные векторы начальных состояний

a={[-1.5; -1.5]+3*rand(2,1)};

Случайные векторы имеют координаты, равномерно распределенные от -1.5 до +1.5. Таким образом, точки начальных состояний располагаются случайным образом в квадрате с координатами вершин (-1.5, -1,5), (-1.5, 1,5), (1.5, 1,5), (1.5, -1,5). Результат представлен на рис. 5.4.

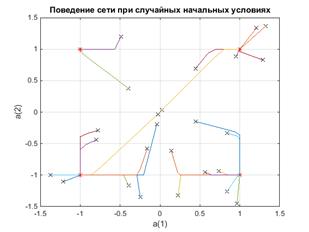
Рис. 5.4. Поведение сети при случайных начальных условиях

В зависимости от начального состояния сеть за 50 шагов переходит в одну из точек равновесия.