В.3 Оценка железобетонного сечения, находящегося под действием изгибающего момента и продольного усилия, посредством определения кривизны

В.3.1 Продольный изгиб колонн при пожаре

(1) Требования настоящего пункта распространяются на железобетонные колонны, на конструкцию которых влияют воздействия по теории второго порядка.

(2) Воздействиями по теории второго порядка для колонн не допускается пренебрегать при пожаре, как при нормальной температуре. Повреждение внешних слоев под воздействием высокой температуры пожара совместно с понижением модуля упругости внутренних слоев ведет к потере устойчивости конструкции.

(3) Оценку колонн при пожаре допускается производить как отдельных конструкций (элементов) посредством определения кривизны (см. раздел 5 EN 1992-1-1) с учетом следующих правил.

(4) Для связевых конструктивных систем непрямые воздействия пожара не учитываются, если не рассматривается снижение моментов по теории первого порядка вследствие снижения устойчивости колонн.

(5) Допускается расчетную длину колонны при пожаре l_0,fi принимать по расчету для нормальной температуры равной l₀. Для более точной оценки допускается учитывать увеличение соответствующей реакции на концах колонн вследствие уменьшения их жесткости. Для этого допускается использовать приведенное поперечное сечение колонны согласно В.2. Эквивалентная жесткость приведенного сечения бетона в данном случае определяется по формуле

,

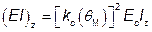где k_c(q_M) —коэффициент снижения сопротивления бетона в точке М;

Е_с — модуль упругости бетона при нормальной температуре;

I_z — момент инерции приведенного поперечного сечения.

Модуль упругости арматуры принимается Е_s,q (см. таблицы 3.2а и 3.2b).

В.3.2 Метод оценки огнестойкости сечений колонн

(1) Данный метод применим для оценки колонн только в связевых конструктивных системах.

(2) Определение расположения изотерм для стандартного температурного режима и параметричес­кого воздействия пожара.

(3) Деление поперечного сечения на зоны с приблизительными средними показателями температуры 20 °С, 100 °С, 200 °С, 300 °С, …, 1100 °С (рисунок В.6).

(4) Определение ширины w_ij, площади A_cij и координат x_ij y_ij для середины каждой зоны.

(5) Определение температуры арматурных стержней. Температура отдельных арматурных стержней определяется для точки в их центре по температурным профилям (см. приложение А) или для справочной информации.

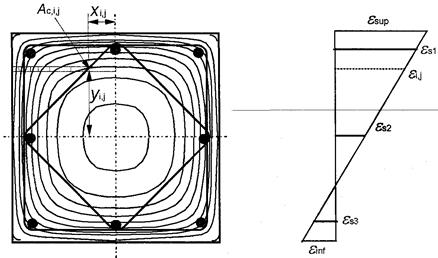
Рисунок В.6 — Разделенное на зоны поперечное сечение колонны

(6) Построение диаграммы «момент-кривизна» для N_Ed,fi с использованием для каждого арматурного стержня и каждой зоны бетона соответствующей диаграммы деформирования согласно 3.2.2.1 (см. рисунок 3.1 и таблицу 3.1), 3.2.3 (см. рисунок 3.3 и таблицу 3.2), и при необходимости, 3.2.4
(см. таблицу 3.3) и 3.2.2.2.

(7) Определение для N_Ed,fi с использованием численных методов предельного изгибающего момента сечения M_Rd,fi и номинального момента по теории второго порядка M_2,fi для соответствующей кривизны.

(8) Определение для установленного воздействия при пожаре N_Ed,fi предельного момента по теории первого порядка M_0Rd,fi как разницы между предельным изгибающим моментом сечения M_Rd,fi и номинальным моментом по теории второго порядка M_2,fi — см. рисунок В.7.

(9) Сравнение предельного момента по теории первого порядка M_0Rd,fi с расчетным изгибающим моментом M_0Еd,fiпо теории первого порядка при пожаре.

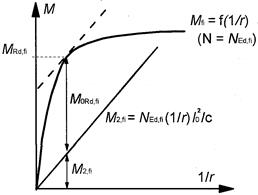
с — зависимый от кривизны коэффициент (» 10), см. 5.8 EN 1992-1-1, M_0Rd,fi ³ M_0Еd,fi

Рисунок В.7 — Диаграмма «момент — кривизна» для определения M_Rd,fi, M_2,fi и M_0Rd,fi

Приложение С

(справочное)