II.2 Расчёт эпюры контактных напряжений
Цель сбора нагрузок - вычисление эпюры контактных напряжений под подошвой сооружения. Вычисление производится по формуле внецентренного сжатия:
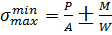 ; (
; ( 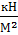 )
)
Где Р-сумма всех вертикальных сил
М- суммарный момент (кНм.)
А=BL-площадь подошвы (м2); L-длина=1пог.м,
B-ширина сооружения (м)
W-момент сопротивления сечения, вычисляется по следующей формуле:
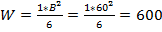 (м3)
(м3) 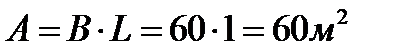
σmax= 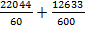 =388,5 (
=388,5 ( 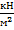 ) σmin=
) σmin= 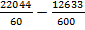 =346,3 (кН/м2)
=346,3 (кН/м2)
Проверка значений эпюры контактных напряжений:
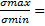 1,12 < 1,5 следовательно необходимо сделать анкерный понур.
1,12 < 1,5 следовательно необходимо сделать анкерный понур.
вычисленные значения σmax и σmin позволяют построить простейшую линейную эпюру контактных напряжений, которая имеет вид трапеции. К эпюре предъявляются определенные требования: σср ≤ R ; σmax ≤ 1.2R, где R-расчетное сопротивление
II.3 Сравнение полученных значений контактных напряжений с характерными напряжениями кривой s=f(p)
Расчетное сопротивление: 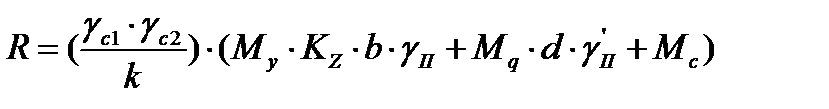 (кПа)
(кПа)
где γс1 и γс2- коэффициенты условий работы грунтового основания и сооружения во взаимодействии с основанием (γс1=1,4 ; γс2=1,4) ;
К=1,-коэффициент, зависящий от ϕ и с.
b-ширина подошвы фундаментной части сооружения (b=B=60 (м) ширина сооружения), КZ=Z0/b+0,2- коэффициент, зависящий от ширины B, здесь Z0=8 м, т.к. b>10 м ( KZ=3,3);
d-глубина заложения фундамента (d=13,1 м);
γII=γIIsb- осредненное расчетное значение удельного веса грунтов, залегающих ниже подошвы фундамента и находящихся во взвешенном состоянии, поскольку выше и ниже фундамента находится один и тот же грунт то (γ11= γIIsb= γ’II =6,36 кН/м3);
Мγ, Мqи Мс- безразмерные табличные коэффициенты, зависящие от угла внутреннего трения грунта (Мγ=1,55, Мq=7,02 и Мс=9,22)
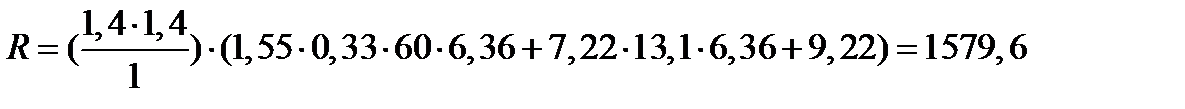 (кН/м2)
(кН/м2)
σср=367,4 < R=1579,6 (кН/м2); σmax=388,5 < 1,2 R=1895,5 (кН/м2)
Для более полного представления о работе основания гидротехнического сооружения также вычисляем начальную критическую и предельную нагрузки (нач.РКР ; РU).
Начальная РКР:
Вычисляется по формуле Пузыревского:
РКР= 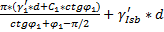 =
= 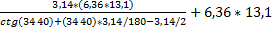 =596,3 (кПа)
=596,3 (кПа)
Предельная нагрузка Pu:
РU=Nϒ ϒI b+Nq q+NC CI
где Nϒ; Nq; NC- безразмерные табличные коэффициенты, зависящие от угла внутреннего трения ϕI грунта основания и от угла отклонения δ предельной нагрузки РU от вертикали. Принимаются по таблице СНиП 2.02.02-85. Т.к предельная нагрузкаРU сравнивается со средним вертикальным сжимающим напряжением σпод подошвой сооружения, то коэффициенты Nϒ; Nq; NC принимаются при δ=0 (Nϒ=24,72; Nq=30,5;)
γI- удельный вес грунта основания ниже подошвы фундамента (γI=6,36) (выше отметки подошвы верхового зуба γI’=γIsb’(γI’=γIsb’=6,36), b-ширина нагрузки (b=B=60м)
q-пригрузка на поверхности III зоны потенциальной призмы выпирания (поверхность призмы на отметке подошвы верхового зуба).q3=(qВ+qгр+n), где:
q=(qВ+qгр)=25,4+56=81,4(кН/м2)
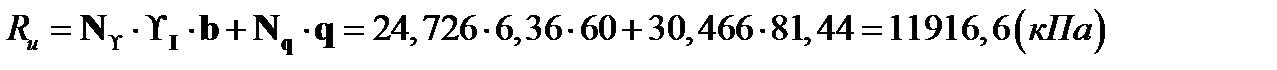
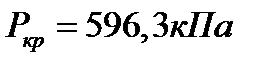
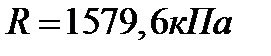
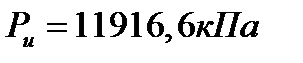
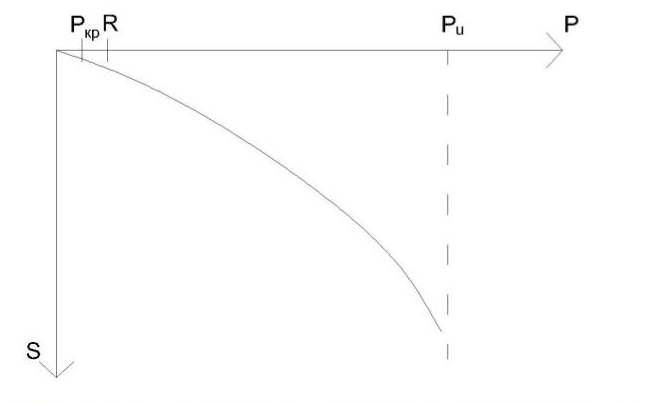
Рис.2 График кривой s=f(p)
III. Расчет основания по I группе предельных состояний
(по прочности основания и устойчивости сооружения).
Критерием обеспечения устойчивости сооружения является условие первого предельного состояния:
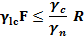
Где F; R-расчетные значения соответственно обобщенных сдвигающих сил и сил предельного сопротивления или моментов сил, стремящихся повернуть (опрокинуть) и удержать сооружение.
γс- коэффициент условий работы, принимаемый по табл.5 СНиП 2.02.02-85, для ж/б плотин и зданий ГЭС γс=1,0
γn- коэффициент надежности по степени ответственности сооружения (γn=1,25)
γlc- коэффициент сочетания нагрузок, принимаемый γlc=1,0
При расчете прочности основания и устойчивости гидротехнического сооружения необходимо:
1) Проверить выполнение условия 1и определить коэффициент запаса устойчивости сооружения при плоском сдвиге сооружения по основанию.
2) Проверить выполнение условия 1и определить коэффициент запаса устойчивости при глубинном сдвиге сооружения.
Потеря устойчивости гравитационных сооружений на нескальных
основаниях возможна по схемам плоского, смешанного и глубинного сдвигов.
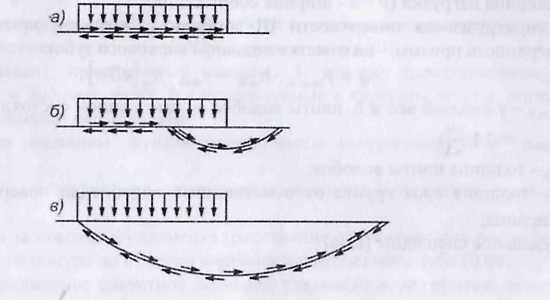
Рис. 3 Виды возможных сдвигов при потере устойчивости гравитационных сооружений на нескальных основаниях: а) плоский: 6) смешанный; в) глубинный сдвиг.
III.1 Плоский сдвиг
Определение расчетной плоскости сдвига для плотин и зданий ГЭС производится по
СНиП 2.02.02-85.
Сдвигающая сила F и сила предельного сопротивления основания R, которая при плоском сдвиге обозначается Rpl,определяется по формулам:
F=Thw +Eawh -Twt
R=Rpl=P tgϕ1+ γ’c Etpw
Где F- расчетное значение сдвигающей силы.
Thw –расчетное значение гидростатического давления воды со стороны верхнего бьефа над понуром и сумма сил гидростатического и фильтрационного давлений воды под понуром (Thw = Thw,н + Thw,п + Thф,п =3782+600+1052=5434 кН)
Eawh – расчетное значение горизонтальной составляющей активного давления грунта с верховой стороны сооружения (Eawh=133,11)
Twt – расчетное значение давления воды со стороны нижнего бьефа (Twt=782)
Rpl – расчетное значение предельного сопротивления при плоском сдвиге
Р- сумма вертикальных расчетных нагрузок, включая противодавление (Р=22044)
tgϕ1 - характеристика прочности грунта по расчетной поверхности сдвига (tgϕ1=0,6914)
Etpw- расчетное значение горизонтальной составляющей пассивного давления грунта с низовой стороны сооружения (Etpw=1418,4)
γс’- коэффициент условий работы, учитывающий зависимость пассивного давления грунта от горизонтального смещения сооружения при потере им устойчивости (γс’=0.7)
F=Thw +Eawh -Twt=5434+133,11-782=4785,11 кН
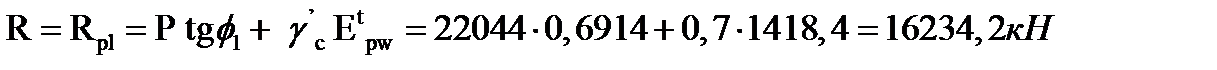
γlc F=4785,11 ≤ 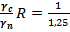 16234,2 = 12987,4 - условие I предельного состояния выполняется
16234,2 = 12987,4 - условие I предельного состояния выполняется
III.2 Глубинный сдвиг
Расчет на глубинный сдвиг основан на теории предельного равновесия. При действии на сооружение предельной нагрузки в грунте основания возникает область предельного напряженно деформированного состояния (потенциальная призма выпирания).
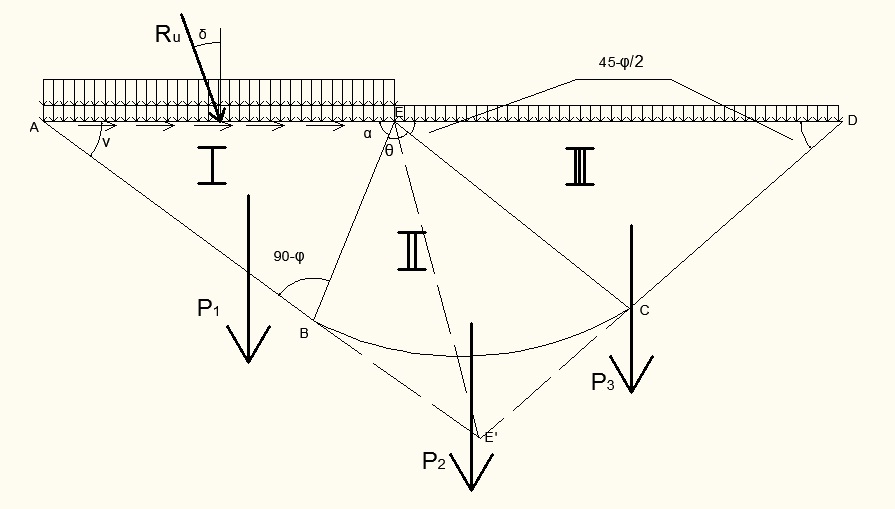
Рис.4 Очертание призмы выпирания
Для выполнения построения очертания призмы выпирания необходимо определить угол ν, который зависит от угла внутреннего трения ϕ1 =340 40’ грунта основания и угла наклона δ от вертикали силы предельного сопротивления сдвигу RU. Угол вычисляется следующим образом: 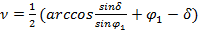
А также угол α=90+ϕ1-ν. Находим длины сторон АВ и ВЕ треугольника АВЕ, используя теорему синусов, и его площадь: АВ= 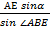 ; ВЕ=r0=
; ВЕ=r0= 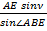 ;
; 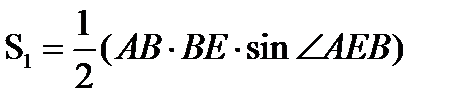
Зона II образуется углом ВЕС и замыкающей его логарифмической спиралью, уравнение которой r=r0eθtgϕ, где r-текущий радиус, r0-начальный радиус спирали (r0=BE). Конечный радиус (отрезок ЕС) вычисляется при угле θ= 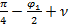
Промежуточные значения угла θ для построения логарифмической спирали: θ1=0,25θ; θ2=0,5θ;θ3=0,75θ
Площадь S2 вычисляется интегрированием уравнения логарифмической спирали от значения угла θ=0 до конечного значения θ по формуле: S2= 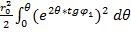 , S2=
, S2= 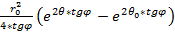
Конечный радиус спирали r является также стороной EC равнобедренного треугольника ECD, образующего III зону призмы выпирания, зону пассивного давления. Площадь III зоны выпирания равна: S3= 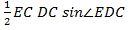 .
.
Все изложенное выше позволяет получить очертание призмы выпирания ABCDE, её зон I, II, III и численные значения их площадей S1, S2, S3.
Численное значение Ru (предельное сопротивление сдвигу), соответствующее своему углу отклонения δ от вертикали, определяется после получения очертания призмы выпирания и определения собственного веса грунта в объёмах I,II,III зон призмы выпирания P1; P2; P3. Веса определяются следующими формулами:
Р1=S1 1пог.м γIsb
Р2=S2 1пог.м γIsb
Р3=S3 1пог.м γIsb+q3 ED
Оценка прочности и устойчивости основания проводится с использованием графика предельной несущей способности основания τlim=f(σ). Для его построения:
- задаются несколькими значениями δ угла наклона к вертикали предельной нагрузки Rui, при: δ=0; δ=0.1ϕ; δ=0.3ϕ; δ=0.5ϕ; δ=0.7ϕ; δ=0.9ϕ
- для каждого значения определяют очертание области предельного состояния грунта ABCDE (призмы выпирания) и величину предельной силы Rui, при которой наступает предельное равновесие с образованием соответствующей потенциальной призмы выпирания.
Сила предельного сопротивления определяется по формуле:
Rui = 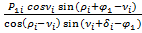
где ρi= 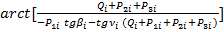
Qi=- 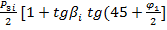
βi= 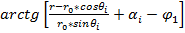
После чего полученные значения Rui раскладывают на нормальную и касательную составляющие σi и τlim по формулам:
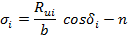
τlimi = 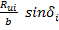
Вычисления для построения призм выпирания, определения предельной нагрузки Ru и построения графика предельной несущей способности основания с помощью ЭВМ
Призма выпирания для δ=0:
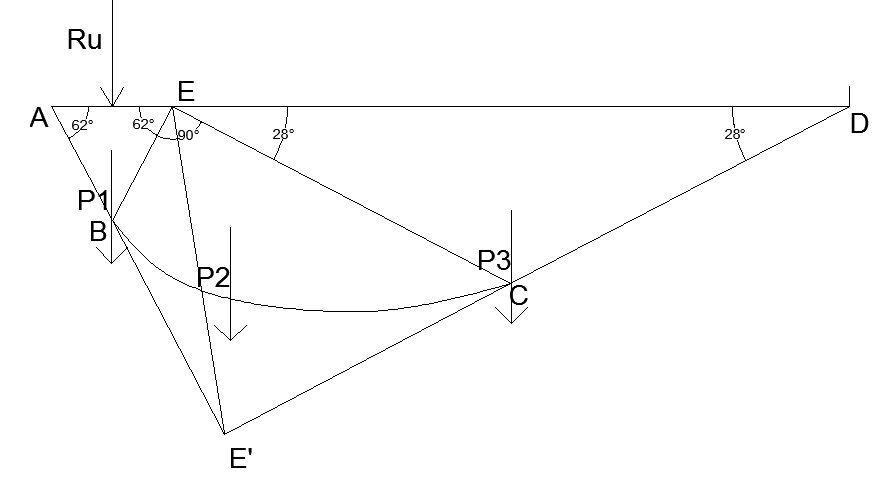
Призма выпирания для δ=0.1ϕ:
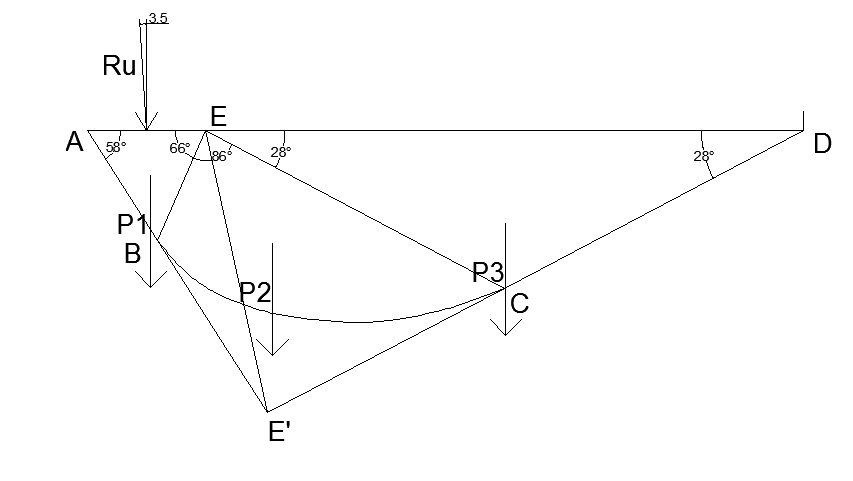
Призма выпирания для δ=0.3ϕ:
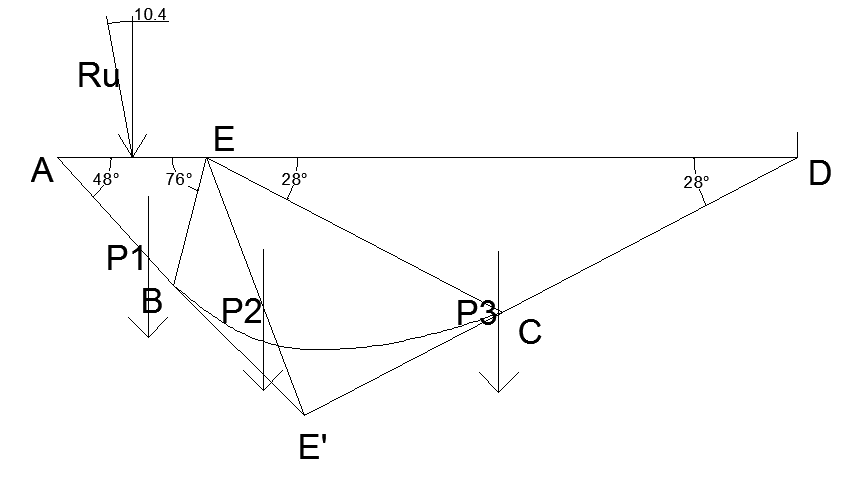
Призма выпирания для δ=0.5ϕ:
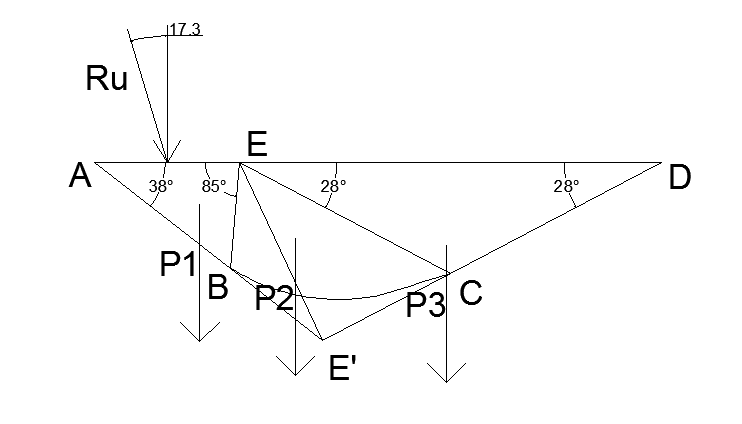
Призма выпирания для δ=0.7ϕ:
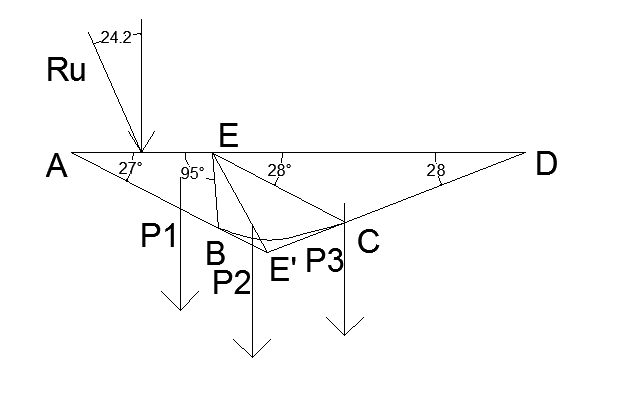
Призма выпирания для δ=0.9ϕ:
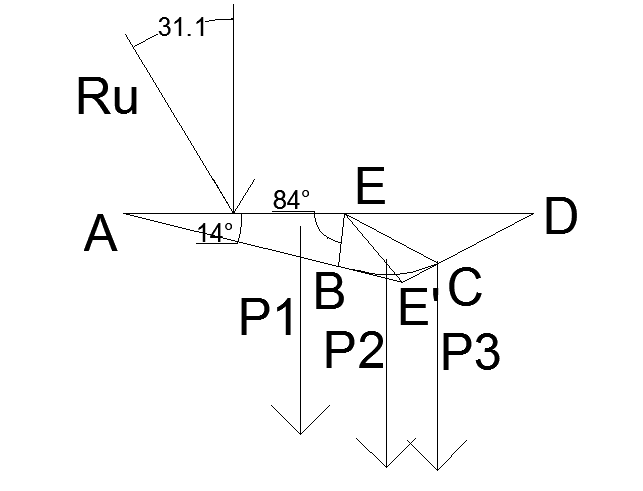
Рис.5 Очертание призмы выпирания при различных значениях δ
III.3 Смешанный сдвиг
Проверка прочности и устойчивости при смешанном сдвиге в курсовом проекте не проводится. При смешанном сдвиге предельное состояние в основании с образованием призмы выпирания возникает не под всем сооружением, а только под низовой частью подошвы. На остальной части подошвы имеет место плоский сдвиг.
IV. Расчет основания по II группе предельных состояний
(расчет по деформациям)
В курсовом проекте необходимо:
1. Определить конечную стабилизированную осадку сооруженияs.
2. Рассчитать горизонтальное смещение сооружения u.
Полученные расчетные значения смещений сооружения нужно сравнить с их предельными значениями – проверить выполнение условий 2-го предельного состояния:
s≤suu≤uu
∆s≤∆su∆u≤∆uu
гдеs- расчетное значение стабилизированной осадки, полученное суммированием осадок всех расчетных грунтовых слоев в пределах сжимаемой толщи Hc.
su–предельная осадка.
∆s ;∆su= расчетная и предельная относительная разность осадок.
U-расчетное значение горизонтального смещения.
uu-предельное значение горизонтального смещения.
∆u; ∆uu – расчетная и предельная относительная разность горизонтального смещения.
a) Эпюра начального (до отрыва) природного сжимающего напряжения (природного давления) σZgIвычисляется на дне котлована, середине и подошвы грунтовых слоев по формуле:
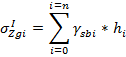
Где γsbi – удельный вес i-го слоя грунта во взвешенном состоянии вычисляется по формуле:
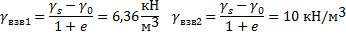
hi – мощность i-го слоя грунта
N – количество вышележащих слоев в пределах сжимаемой зоны HC
γsi – удельный вес твердых минеральных частиц i-го слоя грунта основания
γw – удельный вес воды (γw=10 кН/м3)
б) эпюра разуплотняющего («растягивающего») напряжения 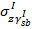
которое частично снижает интенсивность начального природного сжимающего напряжения 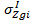 в сжимающей толще HC основания из-за его разгрузки от собственного веса грунта вынутого из котлована глубиной hк. Эпюра имеет максимум на дне котлована
в сжимающей толще HC основания из-за его разгрузки от собственного веса грунта вынутого из котлована глубиной hк. Эпюра имеет максимум на дне котлована 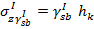 , где начальное природное напряжение снижается до нуля. При увеличении глубины ниже дна котлована ординаты эпюры уменьшаются. Их вычисляют по формуле:
, где начальное природное напряжение снижается до нуля. При увеличении глубины ниже дна котлована ординаты эпюры уменьшаются. Их вычисляют по формуле: 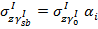 , где коэффициент αi определяется следующим образом:
, где коэффициент αi определяется следующим образом: 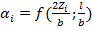
в) эпюра природного сжимающего напряжения σzg , образовавшаяся после разработки котлована и разгрузки основания от собственного веса грунта, вынутого из котлована. Её ординаты являются разностью численных значений ординат эпюр «а» и «б». Верхняя ордината на отметке дна котлована σZg0=0
д) эпюра сжимающих напряжений σzγiI от части нагрузки, создаваемой сооружением, равных давлению о собственного веса грунта вынутого из котлована глубиной hк: pI= σzγiII=γI hk. Является копией эпюры «б», но в отличие от нее-эпюрой уплотняющих сжимающих напряжений(повторное нагружение). Численные значения её вычисляются с использованием коэффициента α.
е) эпюра дополнительного (к природному) сжимающего напряжения 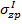 , возникающего в основании сооружения после окончания строительства и достижения им конечного значения p=σср, создаваемого построенным объектом. Ординаты этой эпюры вычисляются по формуле
, возникающего в основании сооружения после окончания строительства и достижения им конечного значения p=σср, создаваемого построенным объектом. Ординаты этой эпюры вычисляются по формуле 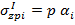 .
.
ж) эпюра сжимающих напряжений σzqwна центральной оси Z, образующаяся от суммарной пригрузки q+wв верхнем бьефе. Ординаты эпюры вычисляются с использованием коэффициента влияния KZ по формуле: 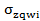 = qw Кz
= qw Кz
где q — среднее значение интенсивности пригрузки от собственного веса понура,
w - среднее значение пригрузки от воды на его поверхности. Ординаты
откладываются вправо от огибающего контура эпюры «е».
з) Эпюра сжимающих напряжений 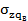 , возникших на центральной
, возникших на центральной
оси Z от пригрузки, создаваемой водобоем qвв нижнем бьефе. Ее ординатына
расчетной схеме добавляются к суммарной эпюре 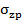 и
и 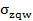 и откладываются
и откладываются
вправо от огибающего контура этой суммарной эпюры. Ординаты эпюры «з»
вычисляются аналогично ординатам эпюры «ж» с использованием коэффициента
влияния Кz, Приложение, таблица 11. по формуле: 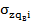 = qв Кz.
= qв Кz.
и) Суммарная эпюра, полученная в результате сложения ординат эпюр «е», «ж» и «з» на расчетной схеме обозначена 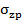 :
: 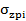 =
= 
Расчет эпюр приведен в табличной форме по вышеизложенным правилам: Таблице IV.1;2;3
Таблица IV.1 Вычисление напряжений от действия собственного веса грунта
| № слоя | Удельный вес грунта ɣ, кН/м³ | Мощность слоя, м | Глубина h, м | Приращение глубины Δh, м | Эпюра "а" | Эпюра "в" | Эпюра "г" |
| 6,36 | |||||||
| 82,7 | 32,2 | 16,1 | |||||
| 114,5 | 64,4 | 32,2 | |||||
| 274,5 | |||||||
| 434,5 | 119,5 |
| x/b=1 | xп/bп=1,5 | xв/bв=1,5 | |||||||||||
| z/b | Kz | Z | z/bп | K zп | 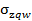 | z | z/bв | K zв | 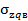 | 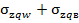 | |||
| 0,25 | 0,02 | 0,165 | 0,16 | ||||||||||
| 0,5 | 0,08 | 0,329 | 0,006 | 0,37 | 0,33 | 0,0065 | 0,364 | 0,734 | |||||
| 0,75 | 0,15 | 0,855 | 0,05 | 3,08 | |||||||||
| 0,86 | 0,052 | 2,912 | 5,992 | ||||||||||
| 0,19 | |||||||||||||
| 1,25 | 0,2 | 1,38 | 0,12 | 7,4 | 1,4 | 0,122 | 6,832 | 14,23 | |||||
Таблица IV.2 Вычисление влияния пригрузок от понура и водобоя на величину вертикальных сжимающих напряжений по центральной оси сооружения
Таблица IV.3 Вычисление ординат эпюр сжимающих напряжений в расчетной схеме для определения осадки
| z | ξ=2z/b | α | Эпюра "б" и "д" | Эпюра "е" | Эпюра "ж" | Эпюра "з" | ординаты суммарной эпюры (5+6+7) | "8"-"4" |
| 367,4 | 367,4 | 316,4 | ||||||
| 0,16 | 0,99 | 50,5 | 364,02 | 364,02 | 313,5 | |||
| 0,33 | 0,982 | 50,1 | 360,8 | 0,37 | 0,364 | 361,5 | 311,4 | |
| 0,86 | 0,875 | 44,6 | 321,48 | 3,08 | 2,912 | 327,5 | 282,9 | |
| 1,4 | 0,698 | 35,6 | 256,6 | 7,4 | 6,832 | 270,9 | 235,3 |
Таблица IV.3 Вычисление ординат эпюр сжимающих напряжений в расчетной схеме для определения осадки Продолжение
| Модуль деформации Esi, кПа | Модуль деформации Epi, кПа | Осадка Ssi , см | Осадка Spi , см | Слои грунта |
| Esl | Epl | 0,43 | 3,5 | I Песок Средней плотности |
| 105500,3 | 78696,5 | ∑Sl=3,93 | ||
| Esll | Epll | 0,39 | 2,7 | II Песок Средней плотности |
| 286971,4 | ∑Sll=3,09 |
Формула для расчета осадки
Формула учитывает изменение НДС основания в процессе строительства. Конечная осадка S сооружения на нескальном основании, при среднем давлении рпод подошвой не превышающем расчетного сопротивления R, вычисляется методом послойного суммирования в пределах сжимаемой толщи Нспо формуле:
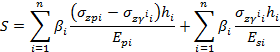
Где:
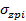 - дополнительное к природному вертикальное нормальное напряжение в середине i-того слоя на глубине Z, основания от нагрузок и пригрузок по вертикали, проходящей через центр подошвы сооружения (суммарные ординаты эпюр «е», «ж», «з»);
- дополнительное к природному вертикальное нормальное напряжение в середине i-того слоя на глубине Z, основания от нагрузок и пригрузок по вертикали, проходящей через центр подошвы сооружения (суммарные ординаты эпюр «е», «ж», «з»);
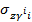 - напряжение в середине i-того слоя на глубине Z, от давления q=
- напряжение в середине i-того слоя на глубине Z, от давления q= 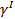 * hк, создаваемого сооружением на отметке дна котлована (подошвы фундамента);
* hк, создаваемого сооружением на отметке дна котлована (подошвы фундамента);
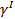 - удельный вес грунта, расположенного выше подошвы сооружения (дна котлована);
- удельный вес грунта, расположенного выше подошвы сооружения (дна котлована);
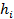 - расчетная толщина i-того слоя грунта;
- расчетная толщина i-того слоя грунта;
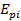 - модуль деформации i-того грунтового слоя, вычисляемый по формуле (1) обязательного приложения 3 СНиП 2.02.02-85 с использованием компрессионного модуля деформации
- модуль деформации i-того грунтового слоя, вычисляемый по формуле (1) обязательного приложения 3 СНиП 2.02.02-85 с использованием компрессионного модуля деформации 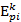 , определяемого по первичной ветви компрессионной кривой этого слоя;
, определяемого по первичной ветви компрессионной кривой этого слоя;
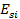 - модуль деформации 1-того слоя грунта, вычисляемый аналогично предыдущему с использованием компрессионного модуля деформации
- модуль деформации 1-того слоя грунта, вычисляемый аналогично предыдущему с использованием компрессионного модуля деформации 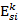 , определяемого по вторичной ветви компрессионной кривой; п- число слоев, на которые разбита сжимаемая толща основания;
, определяемого по вторичной ветви компрессионной кривой; п- число слоев, на которые разбита сжимаемая толща основания;
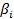 - коэффициент, учитывающий невозможность бокового расширения грунта i-го грунтового слоя, определяемый по формуле:
- коэффициент, учитывающий невозможность бокового расширения грунта i-го грунтового слоя, определяемый по формуле:
νi - коэффициент относительной поперечной деформации г-го слоя грунта.
Формула для S двучленная. В отличие от одночленной, используемой для расчета осадки фундаментов сооружений с глубиной заложения до 5,0 м. Выдаваемые в Заданиях на курсовую работу гидротехнические сооружения заглублены обычно на глубину, превышающую 5,0 м. Они имеют большую опорную площадь. В этом случае учитывается влияние на осадку отрытия глубокого и больших размеров в плане котлована. Появление большого и глубокого котлована изменяет НДС основания в результате разгрузки от давления грунта вынутого из котлована.
Разгрузка уменьшает интенсивность природного давления 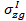 , существовавшего до разработки котлована. На дне котлована оно снижается до нуля. Ниже дна (подошвы будущего сооружения) снижение распространяется на большую глубину, превышающую мощность сжимаемой толщи основания Нс (эпюра
, существовавшего до разработки котлована. На дне котлована оно снижается до нуля. Ниже дна (подошвы будущего сооружения) снижение распространяется на большую глубину, превышающую мощность сжимаемой толщи основания Нс (эпюра 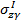 ). Возникшее после выемки грунта из котлована новое сниженное природное НДС основания следует считать исходным для расчета осадки (эпюра
). Возникшее после выемки грунта из котлована новое сниженное природное НДС основания следует считать исходным для расчета осадки (эпюра 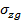 ).
).
В процессе возведения сооружения в отрытом котловане происходит повторное постепенное нагружение основания нагрузкой от возрастающего по ходу строительства его собственного веса. Действие этой нагрузки в формировании осадки разделяется на два расчетных этапа.
Первый этап. Нагружение, возникающее под действием собственного веса строящегося сооружения достигает интенсивности: 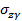 =
= 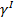 hк. Осадка i-того слоя основания от действия такой нагрузки вычисляется с использованием модуля деформации
hк. Осадка i-того слоя основания от действия такой нагрузки вычисляется с использованием модуля деформации 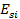 , который определяется по формуле (1) обязательного приложения 3 СНиП 2.02.02-85.
, который определяется по формуле (1) обязательного приложения 3 СНиП 2.02.02-85.
Второй этап начинается после завершения первого этапа, то есть после достижения сжимающим напряжением численного значения равного 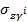 =
= 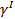 hк - Сооружение продолжает строиться и давление под его подошвой продолжает расти. Заканчивается второй этап после завершения строительства сооружения, когда под его подошвой сжимающее напряжение достигнет максимума
hк - Сооружение продолжает строиться и давление под его подошвой продолжает расти. Заканчивается второй этап после завершения строительства сооружения, когда под его подошвой сжимающее напряжение достигнет максимума 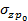 =
= 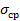 . Осадка 1-того слоя основания от нагрузки (
. Осадка 1-того слоя основания от нагрузки ( 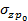 —
— 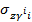 ) на этом этапе вычисляется с использованием модуля деформации
) на этом этапе вычисляется с использованием модуля деформации 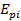 , определяемого по той же формуле обязательного приложения 3 СНиП 2.02.02-85.
, определяемого по той же формуле обязательного приложения 3 СНиП 2.02.02-85.
По результатам компрессионных испытаний находим компрессионные модули деформации 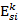 и
и 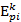 а по ним и модули деформации i-того грунтового слоя (
а по ним и модули деформации i-того грунтового слоя ( 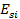 ,
, 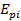 ):
):
Примечание к рис. Петля разгрузкиа повторного нагружения, изображенная на рисунке компрессионной кривой, определяется только экспериментально. В связи с невозможностью выполнения этого в учебной работе, студенту предлагается получить ее ориентировочное очертание самостоятельно. Петля располагается в интервале напряжений 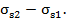 Ветвь разгрузки начинается с точки и практически без увеличения коэффициента пористости продолжается примерно до 2/3 длины интервала. Ни последней трети его длины происходит интенсивное возрастание коэффициента пористости, которое составляет примерно 1/5 часть длины отрезка. Далее из точки строится ветвь повторного нагружения с постепенным понижением коэффициента пористости, где она выходит на ветвь повторного нагружения, по которому проходит дальнейшее нагружение основания в интервале напряжений
Ветвь разгрузки начинается с точки и практически без увеличения коэффициента пористости продолжается примерно до 2/3 длины интервала. Ни последней трети его длины происходит интенсивное возрастание коэффициента пористости, которое составляет примерно 1/5 часть длины отрезка. Далее из точки строится ветвь повторного нагружения с постепенным понижением коэффициента пористости, где она выходит на ветвь повторного нагружения, по которому проходит дальнейшее нагружение основания в интервале напряжений 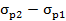 .
.
Для первого грунтового слоя (песчаный грунт):
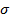 | 0 | 50 | 100 | 150 | 200 | 400 | 600 | 800 |
| E | 0,619 | 0,603 | 0,577 | 0,561 | 0,549 | 0,527 | 0,519 | 0,518 |
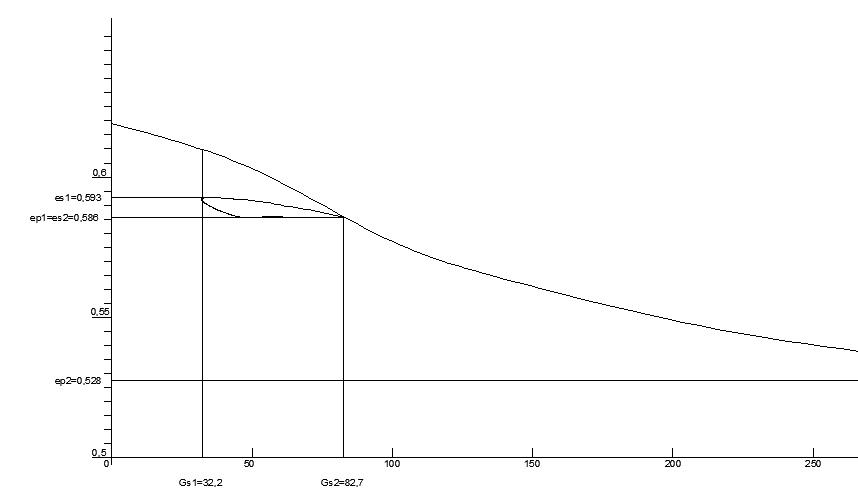
Рис.6 Компрессионная кривая первого слоя
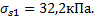
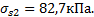
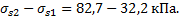
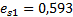
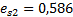
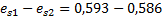
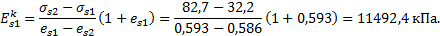
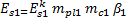
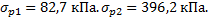
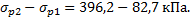
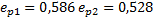
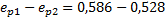
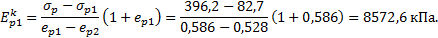
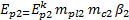
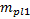 =f(IL;e)
=f(IL;e) 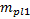 =1
=1 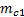 =
= 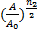
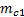 =10,2
=10,2 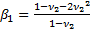 .
. 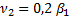 =0.9
=0.9
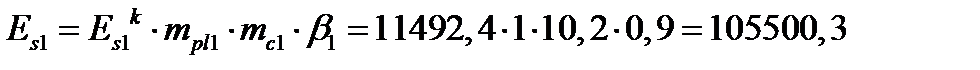 кПа
кПа
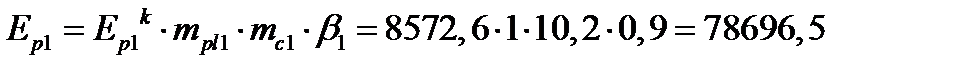 кПа
кПа
Для второго грунтового слоя (песчаный грунт):
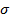 | 0 | 50 | 100 | 150 | 200 | 400 | 600 | 800 |
| E | 0,587 | 0,582 | 0,573 | 0,564 | 0,556 | 0,538 | 0,532 | 0,531 |
Рис.7 Компрессионная кривая второго слоя
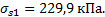
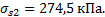
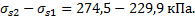
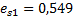
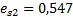
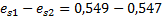
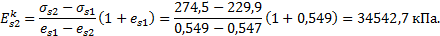
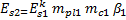
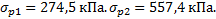
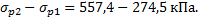
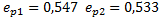
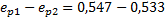
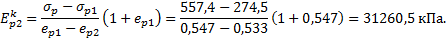
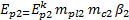
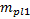 =f(IL;e)
=f(IL;e) 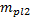 =1
=1 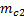 =
= 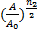
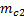 =10,2
=10,2 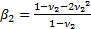 .
. 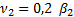 =0,9
=0,9
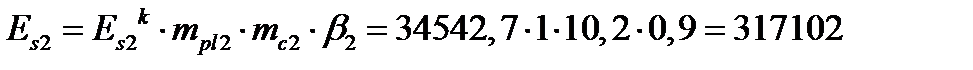 кПа
кПа
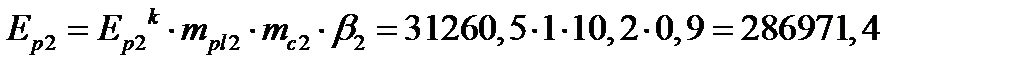 кПа
кПа
Расчет суммарной осадки по сжимаемой толще
:
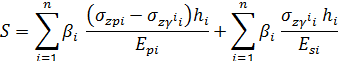
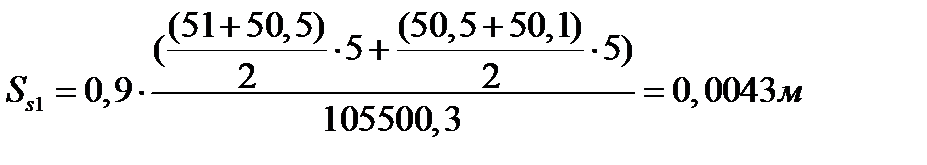
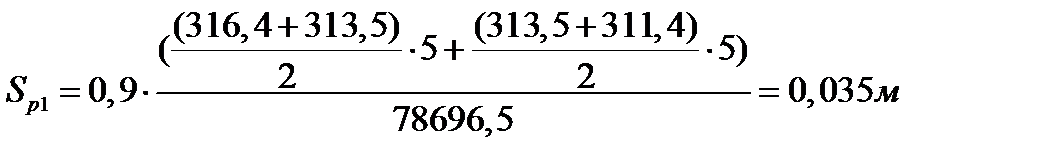
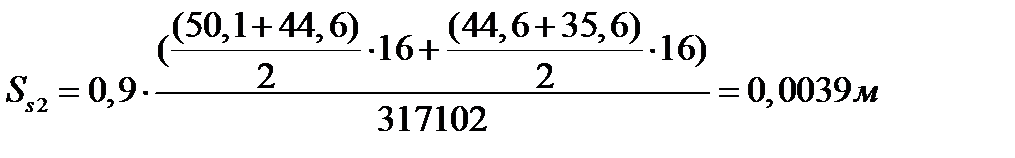
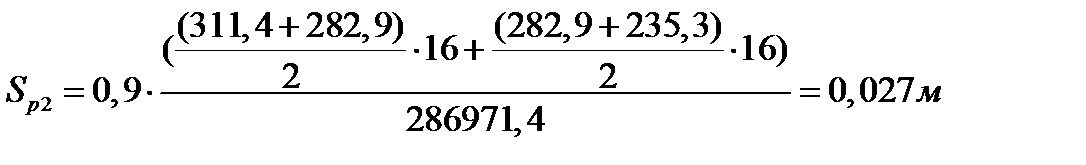
Суммарная осадка по всей сжимаемой толще:
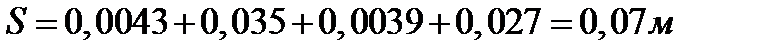
Сравнив полученное осадок значение со значениям осадок в ныне работающих сооружениях делаем вывод, что осадки допустимы. Условие II предельного состояния выполнено.
