Геометрический расчет цилиндрической зубчатой передачи (проектный расчет)

Цель:Научиться определять геометрические параметры в зацеплении зубчатой цилиндрической передачи

Расчет зубчатой закрытой передачи производится в два этапа: первый расчет – проектный, второй – проверочный. Проектный расчет выполняется по допускаемым контактным напряжениям с целью определения геометрических параметров редукторной пары. В процессе проектного расчета задаются целым рядом табличных величин и коэффициентов; результаты некоторых расчетных величин округляют до целых или стандартных значений; в поиске оптимальных решений приходится неоднократно делать пересчеты. Поэтому после окончательного определения параметров зацепления выполняют проверочный расчет. Он должен подтвердить правильность выбора табличных величин, коэффициентов и полученных результатов в проектном расчете, а также определить соотношения между расчетными и допускаемыми напряжениями изгибной и контактной выносливости. При неудовлетворительных результатах проверочного расчета нужно изменить параметры передачи и повторить проверку.

Рисунок 1 - Геометрические параметры цилиндрической

зубчатой передачи

- Определяем межосевое расстояние a_w, мм

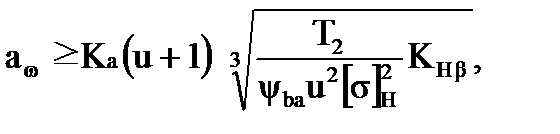(1)

гдеК_а–вспомогательный коэффициент; для прямозубых передач К_а = 49,5;

для косозубых передач К_а = 43

ψ_ва–коэффициент ширины венца колеса, равный 0,28...0,36 - для шестерни, расположенной симметрично относи­тельно опор;

К_нβ – коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев К_нβ =1;

Т₂ – вращающий момент на тихоходном валу, Нм; Т₂ =….;

[σ]_H – допускаемое контактное напряжение колеса с менее прочным зубом, [σ]_H =

u =…. – передаточное число редуктора.

a_w=

Полученное значение межосевого расстояния a_w округляем до ближайшего стандартного числа по таблице 4.4[1].Принимаем a_w=

- Определяем модуль зацепления m, мм

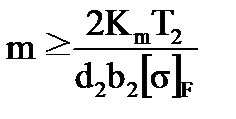, (2)

где К_m-вспомогательный коэффициент; для прямозубых передач К_m= 6,8;

для косозубых передач К_m= 5,8

d₂ - делительный диаметр колеса, мм

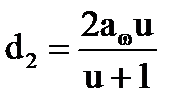(3)

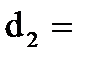(точность 0,00)

b₂ -ширина венца колеса, мм,

b₂ = ψ_ваa_w(4)

b₂ =

Полученное значение округляем в большую сторону до ближайшего целого стандартного числа по таблице 4.4[1].Принимаем b₂ =

[s]_F-допускаемое напряжение изгиба материала колеса c менее прочным зубом, Н/мм²; [s]_F =…

Полученное значение модуля mокругляем в большую сторону до стандартного значения. Принимаем m =

m, мм 1-й ряд: 1,0; 1,5; 2; 2,5; 3; 4; 5

2-й ряд: 1,25; 1,75; 2,25; 2,75; 3,5; 4,5

При выборе модуля 1-й ряд следует предпочитать 2-му.

- Определяем суммарное число зубьев шестерни и колеса:

Для прямозубых колесZ_Σ= 2a_w/ m (5)

Для косозубых колесZ_Σ= (2a_wcos β_min )/ m,

где угол наклона зубьев βmin для косозубых передач, град:

βmin= arcsin(3,5m/ b₂).

В косозубых передачах угол наклона зубьев принимают β = 8… 15°, но из-за роста осевых сил Fа в зацеплении желательно получить его меньшие значения, варьируя величиной модуля m и шириной колеса b₂.

Полученное значение Z_Σ округляем в меньшую сторону до целого числа, принимаемZ_Σ=….

Для косозубых передач уточняем действительную величину угла наклона зубьев:

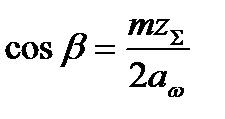
β= arccosβ

Точность вычисления угла β до пятого знака после запятой.

- Определяем число зубьев шестерни

Z₁ = Z_Σ/ (1+u) (6)

Значение Z₁округляем до ближайшего целого числа. Принимаем Z₁ =

Из условий уменьшения шума и отсутствия подрезания зубьев рекоменду­ется

Z₁>18, данное условие выполняется.

- Определяем число зубьев колеса

Z₂ = Z_Σ-Z₁. (7)

Z₂ =

- Определяем фактическое передаточное число u_фи проверяем его отклонение Δu от заданного значения

u_ф=Z₂/Z₁ (8)

u_ф=

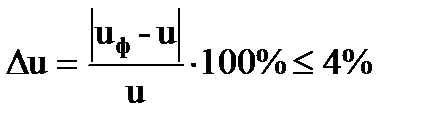(9)

Δu=

При невыполнении нормы отклонения передаточного числа пересчитать Z₁ и Z₂.

- Определяем фактическое межосевое расстояние

a_w= (m·Z_Σ) /2 (10)

8 Определяем фактические основные геометрические параметры передачи, мм

Для прямозубой передачи

Параметр	Шестерня	Колесо
Диаметр, мм	делительный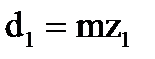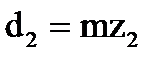
вершин зубьев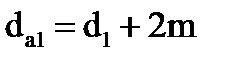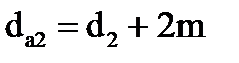
впадин зубьев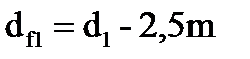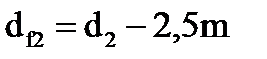
Ширина венца, мм	b1 = b2 + (2…4)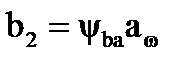

Для косозубой передачи

Параметр	Шестерня	Колесо
Диаметр,мм	делительный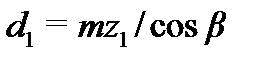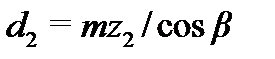
вершин зубьев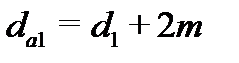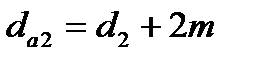
впадин зубьев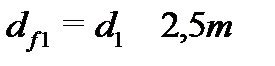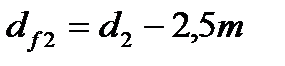
Ширина венца, мм	b1 = b2 + (2…4)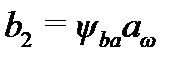

– Дальнейшие расчеты и конструирование ведутся по фактичес­ким межосевому расстоянию a_wи основным параметрам передачи.

– Точность вычисления диаметров колес до 0,01мм

Таблица 4.4 - Предпочтительные числа

Порядковые числа ряда	Ряды предпочтительных чисел	Порядковые числа ряда	Ряды предпочтительных чисел
R5	R10	R20	R40	R5	R10	R20	R40
	1,00	1,00	1,00	1,00		¾	¾	¾	3,35
	¾	¾	¾	1,06		¾	¾	3,55	5,55
	¾	¾	1,12	1,12		¾	¾	¾	3,75
	¾	¾	¾	1,18		4,00	4,00	4,00	4,00
	¾	1,25	1,25	1,25		¾	¾	¾	4,25
	¾	¾	¾	1,32		¾	¾	4,50	4,50
	¾	¾	1,40	1,40		¾	¾	¾	4,75
	¾	¾	¾	1,50		¾	5,00	5,00	5,00
	¾	¾	1,60	1,60		¾	¾	¾	5,30
	¾	1,25	¾	1,70		¾	¾	5,60	5,60
	¾	¾	1,80	1,80		¾	¾	¾	6,00
	¾	¾	¾	1,90		6,30	6,30	6,30	6,30
	¾	2,0	2,00	2,00		¾	¾	¾	6,70
	¾	¾	¾	2,12		¾	¾	7,10	7,10
	¾	¾	2,24	2,24		¾	¾	¾	7,50
	¾	¾	¾	2,36		¾	8,00	8,00	8,00
	2,5	2,5	2,50	2,50		¾	¾	¾	8,50
	¾	¾	¾	2,65		¾	¾	9,00	9,00
	¾	¾	2,80	2,80		¾	¾	¾	9,50
	¾	¾	¾	3,00		10,00	10,00	10,00	10,00
	¾	3,15	3,15	3,15

Примечание. Числа, указанные в таблице, можно как увеличить, так и уменьшить в 10, 100, 1000, 10000, 100000 раз.

ПРАКТИЧЕСКАЯ РАБОТА 4