Предмет и задачи динамического расчета.

Предмет и задачи динамического расчета.

Динамика сооружений – специальный раздел строительной механики, посвященный методам расчета сооружений на динамические нагрузки.

Динамическими нагрузками называются такие, которые во время действия сообщают массам сооружения ускорения, вызывая появление инерционных сил. Если инерционные силы, вызываемые нагрузками, при их приложении малы по сравнению с самими нагрузками, то такие нагрузки приближенно считаются статическими.

Основная задача динамического расчета состоит либо в определении максимальных деформаций и напряжений, вызываемых в сооружении данной динамической нагрузкой, либо в подборе таких размеров сооружения, которые обеспечили бы достаточно малые деформации и напряжения.

Динамическая нагрузка по характеру действия на сооружение значительно сложнее статической. Если действие статических нагрузок определится их величиной, то при расчетах на динамические нагрузки существенную роль играет характер нагрузки.

Динамический расчет проводится на прочность, жесткость, динамическую устойчивость, а также с целью определения амплитуд, скоростей и ускорений колебаний, которые при воздействии на людей и чувствительное оборудование не должны превышать допустимых значений. Кроме этого система проверяется на резонанс при действии динамической нагрузки.

Понятие степени свободы в динамическом сооружении

В динамике сооружение в понятие о степени свободы системы вложен иной смысл. По сравнению с определением в статике.

Значительную роль имеют силы инерции масс: системы бывают с распределенной (континиальные) и сосредоточенной (дискретные).

Континиальная система

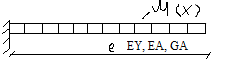n=∞ Силы инерции являются распределенными

Дискретная система

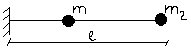
Распределенная масса приведена к двум сосредоточенным. Сам стержень считается невесомым. В данной задаче мы следим только за поведением двух масс, возникают две силы инерции.

Степенью свободы называется число независимых геометрических параметров, определяющих возможные перемещения масс. В целом степень свободы одной сосредоточенной массы равна трем. Каждая масса имеет два независимых линейных смещения и поворот. Континиальную систему можно разбить на бесконечное число точечных масс, т.е. n_д=∞. Для удобства определения числа свободы дискретных систем каждую массу закрепляют линейными стержнями так, чтобы при введенных предпосылках она была неподвижна.

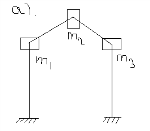
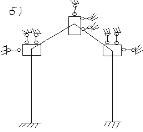
а). расчетная схема

б). n_д=9Схемы для определения степени свободы системы при учете всех возможных смещений масс.

Методы динамики сооружений

В динамике сооружений различают 2 основных метода расчета: кинетостатический и энергетический.

Кинетостатический метод состоит в том, что сооружение рассматривается в равновесии в любой момент времени под действием заданных динамических нагрузок, вызываемых ими инерционных сил, и моментов масс самого сооружения и масс, расположенных на нем. Далее для расчета применяют методы общего курса строительной механики. Энергетический метод основан или на исследовании в условиях равновесия полной потенциальной энергии системы с учетом инерционных сил, или на исследовании кинетической и упругой энергии при движении системы. В частности, когда силы сопротивления движению не учитываются, этот метод основан на законе сохранения энергии: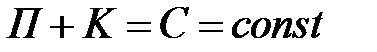

Понятие о резонане

Резонанс-явление резкого возрастания амплитуды вынужденных колебаний в какой-либо колебательной системе, наступающее при приближении частоты периодического внешнего воздействия к некоторым значениям, определяемым свойствами самой системы

Явл-е резонанса возникает при 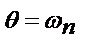,т.е при совпадении частоты возникающей силы с какой-либо из собственных частот системы.

Явл-е резонанса возникает только при 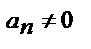т.е если наг-ка содержит состовляющую, пропорциональную кривой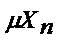

Если этой состовляющей нет резонанса не будет.

Если например наг-ка q(x;t) распределена по пролету семмитрично, а частота 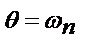явл-е резонанса не должно возникнуть, однако на практике не бывает абсолютно семмитрич-ой наг-ки или что коэфф-т аn сторого = 0

Харак-р явл-я резонанс зависит от св-в колебат-й сис-ы. Наиб. просто резонанс протекает в случаях,когда переодич-му возд-ию подвергается сис-ма с парам-ми не зависящ. от состо-я самой сист-мы.

Резонанс приводит в резкому увелич. амплитуды вынужд-х колеб-й всей констр-ии и может может привести к разруш-ю сооруж-я.

Для устранения его подбир-т св-ва системы так, чтобы нормал-е частоты были далеки от возмож-х частот внеш. возд-я, либо исп-ют явл-е антирезонанса (прим-ют поглатители колебан-й).

Предмет и задачи динамического расчета.

Динамика сооружений – специальный раздел строительной механики, посвященный методам расчета сооружений на динамические нагрузки.

Динамическими нагрузками называются такие, которые во время действия сообщают массам сооружения ускорения, вызывая появление инерционных сил. Если инерционные силы, вызываемые нагрузками, при их приложении малы по сравнению с самими нагрузками, то такие нагрузки приближенно считаются статическими.

Основная задача динамического расчета состоит либо в определении максимальных деформаций и напряжений, вызываемых в сооружении данной динамической нагрузкой, либо в подборе таких размеров сооружения, которые обеспечили бы достаточно малые деформации и напряжения.

Динамическая нагрузка по характеру действия на сооружение значительно сложнее статической. Если действие статических нагрузок определится их величиной, то при расчетах на динамические нагрузки существенную роль играет характер нагрузки.

Динамический расчет проводится на прочность, жесткость, динамическую устойчивость, а также с целью определения амплитуд, скоростей и ускорений колебаний, которые при воздействии на людей и чувствительное оборудование не должны превышать допустимых значений. Кроме этого система проверяется на резонанс при действии динамической нагрузки.