Определение сопротивления судна в сплошных ровных и битых льдах, определение характеристик его ледовой ходкости
Литература
- Ионов Б.П., Грамузов Е.М. Ледовая ходкость судов. СПб: Судостроение, 2001, 512 с.
- Сазонов К.Е. Теоретические основы плавания судов во льдах. СПб.:ЦНИИ им. акад. А.Н.Крылова, 2010, 274 с.
- Цой Л.Г. Морские ледоколы. Особенности проектирования. Учебное пособие. СПбГМТУ, СПб., 2003, 110 с.
Общие пояснения
При проектировании ледоколов и судов активного ледового плавания, а также при разработке различных морских транспортных систем, предназначенных для эксплуатации на замерзающих акваториях, одним из важнейших моментов является определение ледового сопротивления, испытываемого судном при движении во льдах. Многообразие наблюдаемых в реальных условиях различных ледовых образований не позволяет создать расчетные методы определения ледового сопротивления для всех них. Поэтому в морской ледотехнике принято определять ледовое сопротивление для так называемых эталонных ледовых условий. Принято считать, и это подтверждается практикой эксплуатации судов во льдах, что хорошие показатели ледовой ходкости проектируемого судна в эталонных условиях обеспечивают ему эффективность во всем многообразии ледовых условий. К эталонным ледовым условиям обычно относятся следующие: сплошной ровный ледяной покров, мелкобитый лед естественного или искусственного (канал за ледоколом) происхождения, торосистые образования, тертый лед в набитом канале или на акватории порта.
В настоящее время разработано довольно большое количество различных расчетных методов для определения ледового сопротивления судна. Все эти методы можно условно разбить на три большие группы: эмпирические, полуэмпирические и теоретические методы. К эмпирическим методам относятся методы, построенные исключительно на основании обработки данных натурных или модельных экспериментов. Как правило, при анализе таких методов крайне сложно понять, почему тот или иной значимый физический параметр включен в формулу именно таким, а не иным способом. В качестве примера можно привести эмпирическую формулу Л.Г.Цоя для определения предельнойледопроходимости судна.
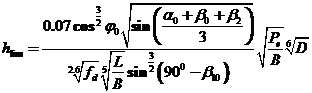 , (2.1)
, (2.1)
где 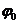 - угол наклона форштевня к конструктивной ватерлинии (КВЛ);
- угол наклона форштевня к конструктивной ватерлинии (КВЛ); 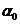 - угол наклона носовой ветви ватерлинии к диаметральной плоскости на 0-ом теоретическом шпангоуте;
- угол наклона носовой ветви ватерлинии к диаметральной плоскости на 0-ом теоретическом шпангоуте; 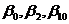 - углы развала шпангоутов на 0-ом, 2-ом и 10-ом теоретических шпангоутах соответственно;
- углы развала шпангоутов на 0-ом, 2-ом и 10-ом теоретических шпангоутах соответственно; 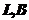 - длина и ширина судна по КВЛ;
- длина и ширина судна по КВЛ; 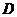 - весовое водоизмещение судна, т;
- весовое водоизмещение судна, т; 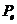 - суммарная тяга гребных винтов на режиме, близком к швартовному, т;
- суммарная тяга гребных винтов на режиме, близком к швартовному, т; 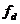 - коэффициент динамического трения корпуса о лед.
- коэффициент динамического трения корпуса о лед.
Формула (2.1) получена на основе обработки данных модельных испытаний серии судов. Эта обработка позволила получить значения численных коэффициентов используемых в формуле. Роль подгоночного коэффициента играет также величина коэффициента трения. Автор рекомендует использовать следующие значения для этого коэффициента: 0.065 – для нержавеющей стали; 0.072 – для покрытия типа "Инерта – 160" и 0.08 для обычной судостроительной стали.
Опыт применения формулы Л.Г.Цоя показывает, что она достаточно хорошо предсказывает предельнуюледопроходимость ледоколов и судов, форма корпуса и главные размерения которых незначительно отличаются от исследованной серии моделей. Если эти параметры существенно отличаются от испытанных в модельном эксперименте, то ошибка может быть значительной. Выражение (2.1) может завышать предельную ледопроходимость крупнотоннажных судов, т.к. в ней содержится сильная зависимость этого параметра от весового водоизмещения.
Основу современного расчета ледового сопротивления судна составляют полуэмпирические и аналитические методы. Различие между ними довольно условное и заключается в большей или меньшей степени использования эмпирического материала. При выводе полуэмпирических формул используется упрощенная математическая модель изучаемого явления. Корреляция результатов расчетов по такой модели с экспериментальными данными достигается за счет введения поправочных коэффициентов, т.е. корректируется вся расчетная модель. В аналитических методах эмпирическая информация используется при разработке моделей физических явления, сопровождающих движение судна во льдах. Из совокупности таких моделей получается расчетный алгоритм, по которому проводятся расчеты.
Все математические модели, созданные для описания ледового сопротивления судна, содержат решение трех основных задач:
§ описание процессов, происходящих при движении ледокола во льдах;
§ определение критериев разрушения ледового покрова и описание картины его разрушения;
§ описание формы поверхности корпуса судна в районе его взаимодействия со льдом.
Уточнение решения указанных задач составляет суть развития методов расчета ледового сопротивления.
Определение ледового сопротивления обычно не является окончательной целью проведения расчетов или экспериментальных исследований. Для праектантовважное значение имеют показатели ледовой ходкости судов. Ледовая ходкость определяется, как возможность судна преодолевать ледовый покров определенной толщины с определенной скоростью, которая задается мощностью главных механизмов. Это понятие, как и в случае движения судна на чистой воде, включает в себя, две составляющие: сопротивление льда движению судна и пропульсивные качества движительного комплекса в ледовых условиях. Основными характеристиками ледовой ходкости являются ледопроходимость, а также кривая ледопроходимости. Под ледопроходимостью понимают предельную толщину сплошного ровного льда, которую может преодолеть судно ледового плавания, двигаясь с минимальной устойчивой скоростью при работе энергетической установки на полную мощность. В качестве минимальной устойчивой скорости обычно принимается скорость движения равная 1,5 – 2 узлам. Кривая ледопроходимости представляет собой зависимость скорости движения судна от толщины преодолеваемого им льда при постоянном значении мощности энергетической установки. Типичный вид кривой ледопроходимости представлен на рис.2.1.
Для получения кривой ледопроходимости необходимо иметь информацию о зависимости ледового сопротивления и тяги движительного комплекса от скорости движения судна. При этом ледовое сопротивление определяется при различных значениях толщины льда. Указанные зависимости наносятся на один график и определяются точки пересечения кривых ледового сопротивления с кривой тяги. По этим точка затем строится кривая ледопроходимости.
Из приведенных выше определений следует, что для определения ледопроходимости судна необходимо уметь определять как его ледовое сопротивление в различных ледовых условиях, так и тягу движительного комплекса в этих же условиях.
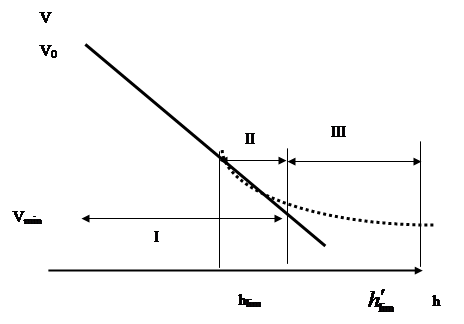 |
Рис. 2.1 Типичный вид кривой ледопроходимости.
V0 – скорость судна на чистой воде; Vmin – минимальная устойчивая скорость движения судна во льдах; hlim – предельная толщина ровного льда, преодолеваемого судном непрерывным ходом (предельная ледопроходимость); 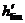 -предельная толщина льда, преодолеваемого судном при движении набегами.
-предельная толщина льда, преодолеваемого судном при движении набегами.
Зона I – судно движется непрерывным ходом в сплошных льдах. Зона II – судно может двигаться непрерывным ходом с небольшой скоростью, либо работать набегами. Зона III – судно может двигаться, работая только набегами.
Ниже будут рассмотрены часто применяемые в настоящее время полуэмпирические формулы для расчета ледового сопротивления, принадлежащие Б.П. Ионову и А.Я.Рывлину. Формула Б.П. Ионова позволяет определить сопротивление судна при его движении в сплошных ровных льдах. Эта формула будет приведена в несколько измененном виде. Изменения касаются последнего слагаемого, входящего в формулу, которое учитывает сопротивление цилиндрической вставки. Для современных крупнотоннажных судов, имеющих цилиндрическую вставку с прямыми бортами, расчет этой составляющей сопротивления осуществляется по методике, предложенной автором этого пособия.
Формула А.Я. Рывлина позволяет рассчитать ледовое сопротивление судна при его движении в битых льдах. Эта формула будет приведена также с изменениями, выполненными автором пособия. Эти изменения касаются перевода формулы из технической метрической системы в систему СИ, аппроксимации графиков, которые используются для расчетов, и расширения использования формулы для больших значений углов входа ватерлинии.
Методика выполнения работы
Аналитическое определение формы ватерлинии и углов наклона шпангоутов
Для выполнения расчетов ледового сопротивления необходимо иметь информацию о форме носовой оконечности судна, включая цилиндрическую вставку, на уровне действующей ватерлинии. При расчетах проектируемого судна эта информация снимается с теоретического чертежа. Для удобства выполнения расчетной работы ниже приводятся формулы для аналитического описания формы ватерлинии судна ледового плавания.
Обобщенно форма для носовой ветви ватерлиниипроизвольного ледокольного судна в системе координат OXY, где начало координат совпадает с миделевым сечением, ось OX направлена в нос, а ось OY на правый борт, может быть задана следующим образом:
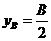 при х < 0,5LPM
при х < 0,5LPM
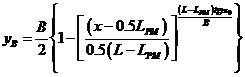 при 0,5L³x³ 0,5LPM, (2.2)
при 0,5L³x³ 0,5LPM, (2.2)
где 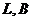 - длина и ширина судна;
- длина и ширина судна; 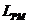 - длина цилиндрической вставки;
- длина цилиндрической вставки; 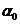 - угол входа носовой ветви ватерлинии.
- угол входа носовой ветви ватерлинии.
Распределение углов наклона шпангоутов для носовой ветви ватерлинии задается следующим выражением:
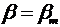 при х < 0,5LPM
при х < 0,5LPM
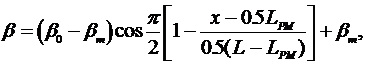 при 0,5L³x³ 0,5LPM(2.3)
при 0,5L³x³ 0,5LPM(2.3)
где 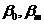 - углы наклона нулевого шпангоута и шпангоута на миделе.
- углы наклона нулевого шпангоута и шпангоута на миделе.
Угол наклона нулевого шпангоута может быть рассчитан по следующей формуле:
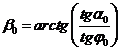 , (2.4)
, (2.4)
где 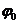 - угол наклона форштевня.
- угол наклона форштевня.
Метод расчета ледового сопротивления с сплошных льдах
В соответствии с методом, предложенным Б.П.Ионовым, расчет ледового сопротивления судна в сплошных льдах выполняется по следующим формулам:
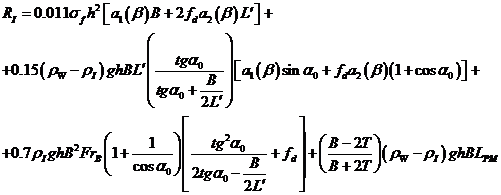 (2.5)
(2.5)
здесь 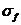 - предел прочности льда на изгиб;
- предел прочности льда на изгиб; 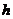 - толщина льда;
- толщина льда; 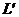 - длина носового заострения;
- длина носового заострения; 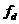 -динамический коэффициент трения льда об обшивку корпуса;
-динамический коэффициент трения льда об обшивку корпуса; 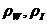 - плотность воды и льда;
- плотность воды и льда; 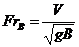 - число Фруда, вычисленное по ширине корпуса судна;
- число Фруда, вычисленное по ширине корпуса судна; 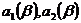 специальные функции формы корпуса судна, зависящие от распределения углов наклона шпангоутов по длине носового заострения, определяемые следующими выражениями:
специальные функции формы корпуса судна, зависящие от распределения углов наклона шпангоутов по длине носового заострения, определяемые следующими выражениями:
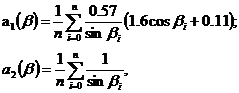 (2.6)
(2.6)
где 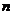 число шпангоутов в пределах носового заострения, которые используются для определения функций формы;
число шпангоутов в пределах носового заострения, которые используются для определения функций формы; 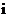 - текущий номер шпангоута. При небольшой длине носового заострения судна для более точного описания зависимостей
- текущий номер шпангоута. При небольшой длине носового заострения судна для более точного описания зависимостей 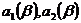 рекомендуется определять углы наклона шпангоутов с шагом ½ или ¼ теоретической шпации. При вычислении выражений (2.6) углы наклона шпангоутов
рекомендуется определять углы наклона шпангоутов с шагом ½ или ¼ теоретической шпации. При вычислении выражений (2.6) углы наклона шпангоутов 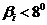 не учитываются.
не учитываются.
В случае, если угол наклона шпангоутов цилиндрической вставки 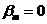 вместо последнего слагаемого в формуле (2.5) необходимо использовать выражение:
вместо последнего слагаемого в формуле (2.5) необходимо использовать выражение:
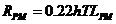 ,
, 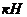 (2.7)
(2.7)
гдеТ – осадка судна.
Примечание: При использовании формул (2.5) – (2.7) необходимо следить за размерностью используемых величин. Если прочность льда на изгиб принимается в МПа, плотность воды и льда должна измеряться в кт/м3, тогда результат расчета будет получен в МН. Если прочность измеряется в кПа, то, соответственно плотность в т/м3 и результат в кН. И наконец, прочность в Па, плотность в кг/м3, результат в Н. При выполнении расчетов по формуле (2.7) в случае использования прочности льда на изгиб в МПа или в Па необходимо соответствующим образом изменить численный коэффициент 0.22.
Метод расчета сопротивления судна в мелкобитых льдах
Для оценок сопротивления битого льда наиболее часто используется полуэмпирическая формула, предложенная А.Я.Рывлиным:
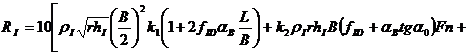 (2.8)
(2.8)
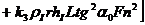
где 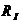 - чистое ледовое сопротивление, т.е. сопротивление битого льда определенное без учета сопротивления воды; r – характерный размер мелкобитого льда, м; hI – толщина мелко битого льда, м; rI – плотность льда, кг/м3; fID – коэффициент трения льда об обшивку корпуса; L - длина судна; В – ширина судна; aВ – коэффициент полноты носовой ветви ватерлинии, который равен
- чистое ледовое сопротивление, т.е. сопротивление битого льда определенное без учета сопротивления воды; r – характерный размер мелкобитого льда, м; hI – толщина мелко битого льда, м; rI – плотность льда, кг/м3; fID – коэффициент трения льда об обшивку корпуса; L - длина судна; В – ширина судна; aВ – коэффициент полноты носовой ветви ватерлинии, который равен
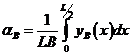 , (2.9)
, (2.9)
здесь 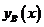 задается формулой (2.2) (интеграл студенты вычисляют самостоятельно); a0 – угол наклона носовой ветви ватерлинии к диаметральной плоскости, град; Fn – число Фруда; k1,k2,k3 – безразмерные эмпирические коэффициента, выбираемые в зависимости от сплоченности льда (см. таблицу 2.1).
задается формулой (2.2) (интеграл студенты вычисляют самостоятельно); a0 – угол наклона носовой ветви ватерлинии к диаметральной плоскости, град; Fn – число Фруда; k1,k2,k3 – безразмерные эмпирические коэффициента, выбираемые в зависимости от сплоченности льда (см. таблицу 2.1).
Таблица 2.1.
Значения эмпирических коэффициентов в формуле (2.8)
| Сплоченность, баллы | |||||
| k1×102 | |||||
| k2 | 2.8 | 5.1 | 8.5 | ||
| k3 | 4.2 | 4.2 | 4.2 | 4.2 | 4.2 |
При проведении расчетов удобнее пользоваться следующими аппроксимационными формулами:
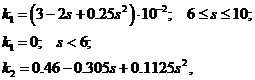 (2.10)
(2.10)
где 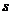 - сплоченность мелкобитого льда в баллах.
- сплоченность мелкобитого льда в баллах.
Среднестатистическое значение параметра rh для природных льдов сравнительно стабильно. В среднем оно равно приблизительно 4 м2. При движении по каналам, проложенным ледоколом в сплошных ровных льдах, величина параметра rh может быть определена по формуле:
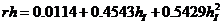 . (2.11)
. (2.11)
При применении формулы (2.8) к судам, имеющим угол наклона носовой ветви ватерлинии к диаметральной плоскости больший чем 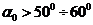 , встречает некоторые затруднения, связанные с тем, что
, встречает некоторые затруднения, связанные с тем, что 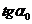 принимает не реально большие значения. Обойти их можно следующим образом. При движении такого тела в мелкобитом льду, например, при буксировке имеющего прямоугольную форму инженерного сооружения, перед его носом формируется зона льда, имеющая треугольную форму в плане, которая буксируется вместе с телом. Протяженность
принимает не реально большие значения. Обойти их можно следующим образом. При движении такого тела в мелкобитом льду, например, при буксировке имеющего прямоугольную форму инженерного сооружения, перед его носом формируется зона льда, имеющая треугольную форму в плане, которая буксируется вместе с телом. Протяженность  этой зоны можно приблизительно рассчитать по следующей формуле:
этой зоны можно приблизительно рассчитать по следующей формуле:
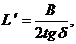 (2.12)
(2.12)
здесь В – характерный поперечный размер движущегося в битых льдах или буксируемого в них тела, d ≈450- угол внутреннего трения битого льда, как сыпучей среды.
Наиболее часто суда движутся в мелкобитом льду, который образовался после прокладки ледоколом канала в различных ледовых условиях. При движении судов по ледяным каналам необходимо различать два возможных их состояния: свежий канал и старый набитый канал. На рис. 2.2 представлены поперечные сечения свежего и старого каналов. Свежий канал образуется сразу же после прохождения ледокола. Старый канал формируется после многократного прохождения по нему судов. Такой канал в основном заполнен тертым льдом.
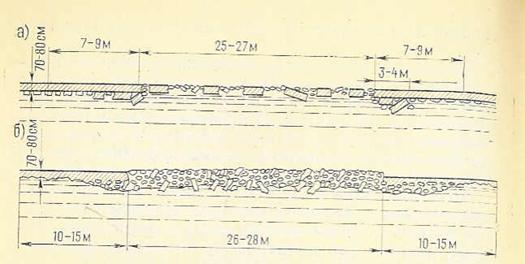
Ри.2.2 - Вид поперечного сечения свежего (а) и старого (б) каналов в припае в зимний период года
Для расчета сопротивления судна при движении по свежему каналу можно использовать формулы (2.8) – (2.12). В этом случае коэффициент 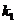 зависит от относительной ширины проложенного ледоколом канала
зависит от относительной ширины проложенного ледоколом канала 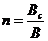 , где
, где 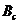 - ширина канала,
- ширина канала, 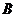 - ширина судна. Зависимость коэффициента
- ширина судна. Зависимость коэффициента 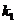 от сплоченности льда и относительного размера канала может быть аппроксимирована следующим выражением:
от сплоченности льда и относительного размера канала может быть аппроксимирована следующим выражением:
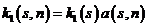 , (2.13)
, (2.13)
где 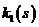 задается формулой (2.10), а
задается формулой (2.10), а 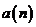 описывается следующим выражением:
описывается следующим выражением:
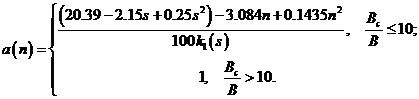 (2.14)
(2.14)
Определение сопротивления воды
При использовании расчетных формул приведенных выше определяется чистое ледовое сопротивление судна, т.е. без учета сопротивления воды. Для выполнения расчетов ледовой ходкости необходим его учет.
В первом приближении при движении судна во льдах испытываемое им сопротивление воды можно представить только из сопротивления трения, т.к. волновая составляющая во льдах практически не реализуется.
Расчет сопротивления воды выполняется по общей формуле, известной из теории корабля:
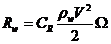 , (2.15)
, (2.15)
где 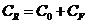 ,
, 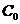 - коэффициент остаточного сопротивления;
- коэффициент остаточного сопротивления; 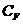 - коэффициент сопротивления трения;
- коэффициент сопротивления трения; 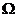 - площадь смоченной поверхности подводной части корпуса.
- площадь смоченной поверхности подводной части корпуса.
Коэффициент трения рассчитывается по формуле Прандтля – Шлихнинга:
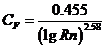 , (2.16)
, (2.16)
где 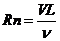 - число Рейнольдса;
- число Рейнольдса; 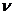 - кинематическая вязкость воды.
- кинематическая вязкость воды.
Смоченная поверхность определяется по приближенным формулам.
Для судов без цилиндрической вставки по формуле С.П.Мурагина:
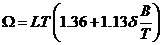 , (2.17)
, (2.17)
где 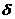 - коэффициент общей полноты.
- коэффициент общей полноты.
Для судов с цилиндрической вставкой по модифицированной формуле С.П.Мурагина:
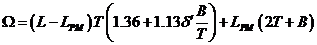 , (2.18)
, (2.18)
где 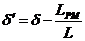 .
.
Полное ледовое сопротивление определяется по формуле:
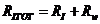 . (2.19)
. (2.19)
Показатели ледовой ходкости судна
Как следует из приведенного в начале определения для определения показателей ледовой ходкости необходимо знать тяговые характеристики движительного комплекса. В данной расчетной работе рассчитывать тяговые характеристики движительного комплекса в соответствии с требованиями теории корабля. Мы воспользуемся эмпирической формулой, которая описывает изменение тяги движительного комплекса 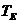 при увеличении скорости движения судна:
при увеличении скорости движения судна:
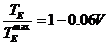 , (2.20)
, (2.20)
где 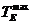 - тяга движителей судна на швартовном режиме,
- тяга движителей судна на швартовном режиме, 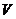 - скорость судна, м/с.
- скорость судна, м/с.
В задании на проектирование судна всегда указывается основная характеристика его ледовой ходкости – предельная ледопроходимость 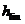 ,т.е. та толщина ровного льда, которую судно преодолевает с минимальной устойчивой скоростью 2 узла (≈ 1 м/с). Выполнив расчет полного ледового сопротивления по формулам (2.5) – (2.7), (2.15) и (2.19) можно определить ледовое сопротивление судна в предельных льдах. Так как принимается, что 2-х узловая скорость устойчивая, можно записать следующее равенство:
,т.е. та толщина ровного льда, которую судно преодолевает с минимальной устойчивой скоростью 2 узла (≈ 1 м/с). Выполнив расчет полного ледового сопротивления по формулам (2.5) – (2.7), (2.15) и (2.19) можно определить ледовое сопротивление судна в предельных льдах. Так как принимается, что 2-х узловая скорость устойчивая, можно записать следующее равенство:
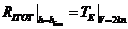 , (2.21)
, (2.21)
из которого с помощью выражения (2.20) можно определить тягу движительного комплекса на швартовном режиме. Затем по формуле (2.20) рассчитать значения тяги при других скоростях движения судна. Таким образом, может быть рассчитана зависимость 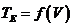 . Эта кривая наносится на график зависимости
. Эта кривая наносится на график зависимости 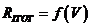 и по точкам их пересечения строится кривая ледопроходимости
и по точкам их пересечения строится кривая ледопроходимости 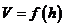 .
.
Исходные данные
Исходные данные для выполнения работы представлены в табл. 2.2, варианты 0 ¸ 9.
Таблица 2.2
| Характеристика | Номер варианта | |||||||||
| Характеристики судна | ||||||||||
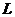 , м , м | ||||||||||
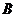 , м , м | ||||||||||
| Т, м | 7,5 | |||||||||
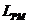 , м , м | ||||||||||
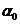 , град , град | ||||||||||
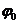 , град , град | ||||||||||
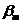 , град , град | ||||||||||
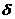 | 0.55 | 0.58 | 0.57 | 0.77 | 0.74 | 0.8 | 0.75 | 0.79 | 0.78 | 0.81 |
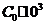 | 1.0 | 1.1 | 1.1 | 1.1 | 1.2 | 1.2 | 1.1 | 1.2 | 1.2 | 1.2 |
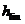 , м , м | 1.5 | 1.7 | 1.7 | 1.5 | 1.8 | 1.5 | 1.6 | 1.7 | ||
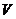 , узлы , узлы | Для ровного льда от 2 до 5 Для битого льда от 2 до 8 Шаг выбирается самостоятельно | |||||||||
| Внешняя среда | ||||||||||
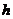 , м , м | От 0.8 до предельной ледопроходимости (шаг выбирается самостоятельно с учетом возможности построения кривой 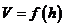 ) ) | |||||||||
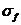 , кПа , кПа | ||||||||||
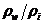 , кг/м3 , кг/м3 | 1015/800 | |||||||||
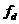 | 0.15 | |||||||||
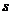 , баллы , баллы | ||||||||||
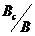 | 1.5 | 1.5 | 1.7 | 1.8 | 1.4 | 1.3 | 1.5 |
Порядок выполнения работы
1. Рассчитать ледовое сопротивление судна в сплошных льдах. Построить графики ледового сопротивления (рис. 2.3). Вычислить величинуа по следующей формуле:
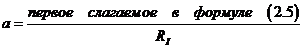 . (2.22)
. (2.22)
Величинааопределяется для наименьшей скорости движения, которая была использована при проведении расчетов ледового сопротивления. Эта величина будет необходима для выполнения расчетной работы № 4.
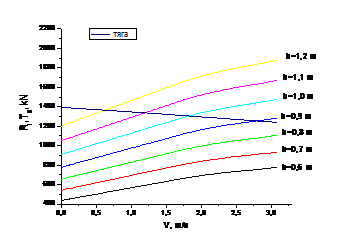
Рис. 2.3 Пример построения графиков ледового сопротивления
2. Рассчитать ледовое сопротивление судна в мелкобитых льдах для условий отсутствия границ и движения по каналу. Построить графики ледового сопротивления.
3. Рассчитать сопротивление воды движению судна. Определить полное ледовое сопротивление. Построить график.
4. Определить тяговые характеристики движительного комплекса. Построить зависимость тяги от скорости движения (рис.2.4).
5. Построить кривую ледопроходимости судна (рис.2.4).
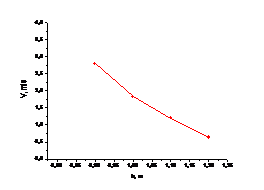
Рис. 2.4 Пример построения кривой ледопроходимости в ровных льдах
Составление отчета
В отчет по лабораторной работе входят построенные по результатам расчетов графики и анализ полученных результатов. Анализ полученных результатов.
Примечание. Результаты выполнения данной работы необходимо сохранить, т.к. они потребуются для выполнения других расчетных работ.
Расчетная работа №3
