Понятие о системе зональных прямоугольных координат в проекции Гаусса-Крюгера.

Система географических координат универсальна и принята от какого-либо начала, может быть распространена на всю сферу, но вычисление координат сложно.

Система прямоугольных координат проста в вычислениях, но ее можно применять при съемке только незначительных по величине участков земной поверхности (с радиусом до 10 км).

Поэтому с 1928 года в СССР и на Украине была введена зональная прямоугольная система координат Гаусса-Крюгера, которая дает возможность использовать систему прямоугольных координат на плоскости для больших по величине территорий, сохраняя связь с геодезическими координатами.

В основу этой системы положена проекция, предложенная немецким ученым Гауссом и разработанная для практического пользования в геодезии Крюгером.

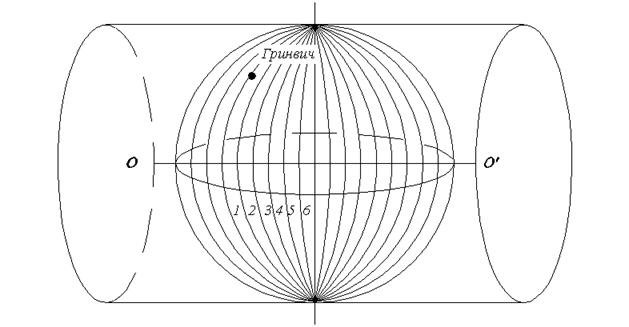Рис.2.4. Схема построения поперечной цилиндрической проекции

Сущность проекции Гаусса состоит в следующем. Земную сферу делят меридианами на шестиградусные зоны (рис.2.4.). Зоны нумеруются с запада на восток от Гринвичского меридиана. Зная номер зоны легко определить средний меридиан, который называется осевым по формуле Z₀ = 6⁰n – 3.

где n – номер зоны. Например, при номере зоны 6, Z₀ = 36° – 3°=33⁰.

В территорию СССР входило 29 зон, начиная с четвертой по тридцать вторую включительно.

Плоское изображение каждой зоны получают путем проектирования ее на боковую поверхность цилиндра (ось которого расположена перпендикулярно земной оси). Затем цилиндр развертывают на плоскость. Осевой меридиан зоны и экватор изображаются прямыми линиями. За ось абсцисс в каждой зоне принимают изображение осевого меридиана, а изображение экватора за ось ординат. Начало координат служит точка пересечения осевого меридиана и экватора. Абсциссы отсчитывают от экватора к северу со знаком плюс и к югу со знаком минус, ордината к востоку от осевого меридиана имеет знак плюс, к западу – минус.

На территории стран СНГ все абсциссы положительны, т.к. страны расположены выше экватора. Для того, чтобы не иметь отрицательных ординат, за начало отсчета по У принято 500 км. Кроме того, впереди каждой ординаты указывают номер зоны, в которой расположена точка.

Так, например, у= 7487230 указывает на то, что точка находится в седьмой зоне и что ее ордината у=487230 м – 500км = - 12770м. Для удобства пользования прямоугольными координатами на карту наносят сетку квадратов, образованную линиями параллельными осям координат, проведенными через 1 или 2 километра. Такую сетку называют километровой.

Условная система прямоугольных координат

При составлении планов и обмерных чертежей архитектурных ансамблей, выносе проектных сооружений на местность, выполнении локальных инженерно-геодезических работ, часто применяют условную систему прямоугольных координат. За начало координат, и направление осей в этой системе принимают произвольно выбранные под 90 градусов направления, удобные для применения.

Полярная система координат

Широко применяется при съемках и разбивках сооружений. Она состоит из полярной оси ОХ, выбранной произвольно, относительно которой положение точки В определяется полярным углом b, измеряемым по ходу часовой стрелки и горизонтальным проложением d (рис.2.5.).

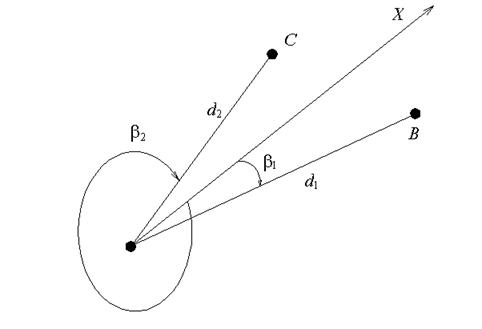Рис.2.5. Полярная система координат

РАЗДЕЛ 3. ОРИЕНТИРОВАНИЕ ЛИНИЙ

Азимуты и румбы

Ориентировать линию – значит определить ее положение относительно принятого исходного направления.

За исходное направление в геодезии принимают направления (географического) истинного, магнитного или осевого меридиана и произвольно закрепленную линию.

Положение линий относительно исходных направлений определяется горизонтальными углами, называемыми азимутами, дирекционными углами и румбами.

Истинным (географическим) азимутом называется горизонтальный угол, образованный северным направлением истинного меридиана и горизонтальным проложением данной линии по часовой стрелке. Азимуты измеряют от от 0⁰ до 360⁰.

Магнитный азимут отсчитывают от северного направления магнитного меридиана. Направление магнитного меридиана определяют при помощи магнитной стрелки буссоли. Угол между истинным и магнитным меридианом называется склонением магнитной стрелки (рис. 3.1).

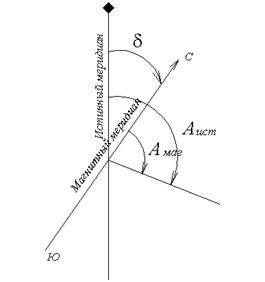Различают восточное и западное склонение, в зависимости от того, к востоку или западу отклоняется северный конец магнитной стрелки от истинного меридиана. Зная магнитный азимут и склонение, можно определить истинный азимут. Если склонение восточное δВ, то Аист. = Амагн. + δВ. Если склонение западное, то Аист. = Амагн. - δВ. Величина склонения в разных точках земной поверхности различна. Различают склонения суточное, годовое и вековое.

Рис.3.1. Азимуты и магнитное склонение

Румбы. На практике часто вместо азимутов пользуются румбами – острыми углами, которые отсчитываются от ближайшего конца (северного или южного) исходного направления до данного направления линии.

Румбы измеряют от 0⁰ до 90⁰. Кроме числового значения румба указываются направление линии относительно стран света, например СВ:30⁰.

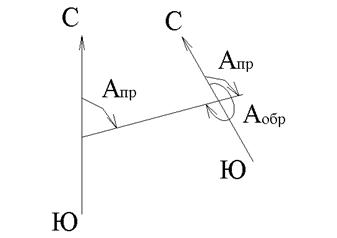	В геодезии принято различать прямое и обратное направления. Так, если линию 1-2 считать прямым направлением, то 2-1 будет обратным направлением той же линии (рис.3.2). А обр.= Апр ± 1800 ± γ , где - γ сближение меридианов, равное γ = ∆λsinφ
Рис.3.2. Прямое и обратное направление.

Магнитный азимут равен А^М_обр =А^М_пр ± 180⁰ ± δ

Дирекционным углом называется горизонтальный угол измеренный по ходу часовой стрелки от положительного направления оси Х до данной линии по ходу часовой стрелки.

α_отр = α_отр ± 180⁰

Рассмотрим связь между азимутами, дирекционными углами и румбами.

Дан азимут или дирекционный угол, требуется определить румб ( рис.3.3)

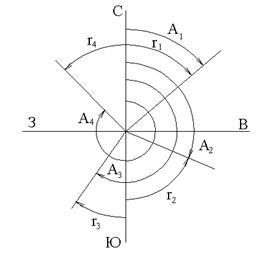	СВ:r1=А1 (I четверть) ЮВ:r2=1800 + А2 (II четверть) ЮЗ:r3=А3 – 1800(III четверть) СЗ:r4= 360 0 – А4(IV четверть) Дан румб, можно определить азимут: А1 = r1 А2 = 180 0 - r2 А3 = 180 0 + r3 А4 = 360 0 - r4
Рис.3.3. Зависимость азимутов, дирекционных углов и румбов.

РАЗДЕЛ 4. ТОПОГРАФИЧЕСКИЕ ПЛАНЫ И КАРТЫ.

4.1. Понятие о плане, карте и профиле.

План – это уменьшенное, подобное изображение на бумаге незначительных участков земной поверхности, без учета кривизны земли.

Карта – это уменьшенное изображение на бумаге значительной по величине территории земной поверхности с учетом кривизны Земли.

При построении карты предполагают, что сначала поверхность Земли изображается на сфероиде определенного размера, а затем с его поверхности переносится на плоскость. Этот перенос сводится к построению на плоскости горизонтальной сетки параллелей и меридианов сфероида, называемой картографической сеткой, внутри которой наносят контуры местности и рельеф.

Математический закон построения картографической сетки на плоскости называется картографической проекцией.

Существенным отличием карты от плана является закономерное изменение ее масштаба от точки к точке, тогда как на плане масштаб постоянен во всех его частях. На картах имеются две системы координат: географическая и прямоугольная, на плане только прямоугольная. По содержанию карты бывают общегеографические и тематические (специальные).

Масштабы

Масштабом называется отношение длины линии на плане карте к длине ее горизонтального проложения на местности.

Масштаб – это степень уменьшения горизонтальных проекций контуров при перенесении их на план или карту с участка местности.

Различают масштабы: численный, линейный и поперечный.

Численный масштаб выражается в виде простой дроби с числителем равным единице. Знаменатель показывает степень уменьшения отрезка линии при перенесении на план. В СНГ применяют следующие масштабы планов и карт:

1 : 500 – 1 см на плане соответствует 5 метрам на местности,

1 : 1000 - -«- 10 -«-

1 : 2000 - -«- 20 -«-

1 : 5000 - -«- 50 -«-

1 : 10000 - -«- 100 -«-

1 : 25000 - -«- 250 -«-

1 : 50000 - -«- 500 -«-

1 : 100000 - -«- 1000 -«- и т.д.

Линейным масштабом называется графическое изображение численного масштаба. Наибольшее деление называется основанием (рис 4.1) Основание масштаба бывает 1 см или 2 см.

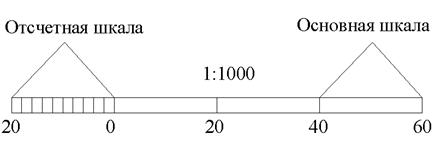Рис.4.1. Линейный масштаб

Поперечный масштаб. Для повышения точности отсчитывания пользуются поперечным масштабом ( рис. 4.2).

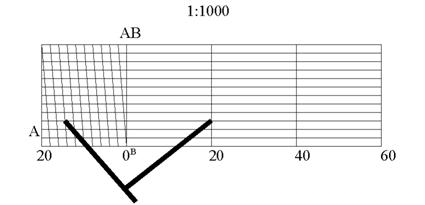Рис.4.2. Поперечный масштаб

За основание масштаба АВ принимают 2 см. Это основание откладывают несколько раз по прямой. В полученных точках восстанавливают перпендикуляры. Левое основание делят на n равных частей (n = 10), перпендикуляры делят на m равных частей (m = 10) и проводят через концы отрезков параллельные основанию линии. Всего горизонтальных линий, считая и основание должно быть одиннадцать. Через левый верхний угол левого основания и первое деление левого нижнего основания проводят наклонную прямую, а затем параллельными наклонными линиями соединяют точки нижнего и верхнего левого основания масштаба. При основании 2 см, n =10, m=10; значение наименьшего деления поперечного масштаба или точность поперечного масштаба t равно:

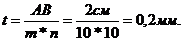
При пользовании поперечным масштабом циркулем берут линию на плане и переносят на поперечный масштаб. Правую ножку циркуля ставят в правой части масштаба на один из перпендикуляров, а левую на ту же горизонтальную линию левого основания и перемещают циркуль вверх до совпадения с целыми делениями, после чего производят отсчет.

Предварительно производят оцифровку поперечного масштаба, так, например, для масштаба 1:1000:

в 1 см – 10 м,

одно деление основания (2 см) – 20 м,

одно деление шкалы по горизонтали (2 мм) – 2 м,

одно деление шкалы по вертикали (0,2 мм) – 0,2 м.

Расстояние, отмеченное на поперечном масштабе рисунка 4.2. составляет 32,6 м.

Точностью масштаба наз. горизонтальное расстояние на местности, соответствующее 0,1 мм на плане или карте данного масштаба. Точность плана в разных масштабахприведена в таблице 4.1.

Таблица 4.1.

Масштаб	Точность масштаба
1:500	0,05 м.
1:1000	0,10 м.
1:2000	0,20 м.
1:5000	0,50 м.
1:10000	1,00 м.

4.3. Содержание топографических карт и планов.

Карта или план состоит из зарамочного оформления, рамки и внутреннего содержания.

Зарамочное оформление включает: номенклатуру (шифр) листа, год издания, масштаб, сечение рельефа, метод съемки, системы координат и высот, величины сближения меридианов и склонения магнитной стрелки.

Рамка карты (плана) содержит координаты углов рамки в географической системе и выходы километровой сетки в прямоугольной системе координат. На планах подписываются углы рамки трапеции только в прямоугольной системе координат.

Содержание карты (плана) состоит в изображении всех элементов земной поверхности (контура, предметы, дороги, водоемы, растительный покров, сооружения, коммуникации и т.д.) – ситуации с использованием масштабных и немасштабных условных знаков, пояснительных надписей, цветовой окраски, принятые едиными для данного государства и неровностей земной поверхности – рельефа, изображенного отметками и горизонталями. Подробность изображения ситуации зависит от масштаба карты или плана (чем крупнее масштаб, тем подробнее карта или план), а рельефа- от сечения (чем меньше сечение, тем подробнее изображен рельеф).

Условные знаки и цвет наглядно показывают содержание тех или иных элементов. Пояснительные надписи и цифровые обозначения дополняют условные знаки, раскрывая особенности изображаемых объектов. Условные знаки бывают масштабные, когда контур изображается в масштабе карты или плана, и внемасштабными (точечными) условными знаками, когда предметы местности и различные объекты имеют малую величину, очертание которых не может изображаться в данном масштабе карты или плана (деревья, столбы, дороги и т.д.).

Рельеф изображается горизонталями коричневого цвета. Горизонталь – это кривая линия равных высот (след сечения горизонтальными плоскостями проведенными через равные высоты – сечения). Рельеф характеризуется сечением и заложением (Рис. 4.3.).

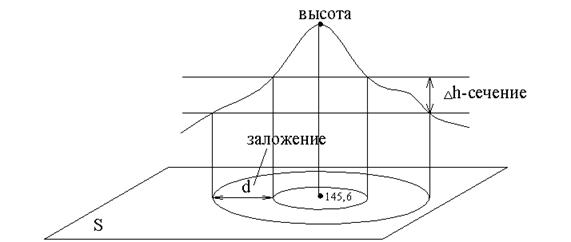Рис.4.3. Изображение рельефа горизонталями

4.4. Номенклатура карт и планов, размеры рамок топографических планов разных масштабов.

При картографировании значительной территории получают много листов карт. В связи с этим вводится система обозначения отдельных листов карт различных масштабов, которая называется номенклатурой карт (буквенно-числовое обозначение листов).

В основу номенклатуры топографических карт положена карта масштаба 1:1000000. Каждый лист такой карты соответствует сферической трапеции размерами 4⁰ широты и 6⁰ долготы.

Для получения границ листов карт масштаба 1:1000000 всю поверхность земного шара разделяют меридианами, проведенными через 6⁰ по долготе на 60 колонн и параллелями, проведенными через 4⁰ начиная от экватора, на ряды или пояса. Колонны совпадают с зонами, но счет зон ведется от нулевого (Гринвичского) меридиана, а счет колонн – на восток от меридиана с долготой 180⁰. Поэтому номера колонн отличаются от номеров зон на 30 единиц.

Ряды или пояса обозначаются заглавными буквами латинского алфавита по направлению от экватора к полюсам. Колонны обозначают арабскими цифрами.

Номенклатура листов карт связана с масштабом карт. Так, территория, которая изображена в масштабе 1:1000000 на одном листе бумаги размером 55 х 55 см может быть изображена в более крупных масштабах на нескольких листах. Одному листу карты масштаба 1:1000000 (Рис. 4.4) соответствует 4 листа карты масштаба 1:500000 (обозначается буквами АБВГ) –N- 37 -А , девять листов карты масштаба 1:300000 (обозначенными от I до IХ, написанными перед номенклатурой миллионного листа, например : IХ – N – 37), 36 листов масштаба 1:200000 обозначенными римскими цифрами от I до ХХХVI, например N – 37 – ХХХVI, написанными после номенклатуры миллионного листа и 144 листам карты масштаба 1:100000, обозначенными арабскими цифрами от 1 до 144 включительно, например: N – 37 – 144. Одному листу карты масштаба 1:100000 (Рис. 4.5.) соответствует 4 листа карты масштаба 1:50000, которые обозначают заглавными буквами русского алфавита А, Б, В, Г. Номенклатура последнего листа М 1:50000 – N – 37 – 144 – Г. Одному листу М 1:50000 соответствует четыре листа карты М 1:25000, которые обозначаются строчными буквами русского алфавита а, б, в, г. Номенклатура последнего листа М 1:25000 – N – 37 – 144 – Г – г. Одному листу карты масштаба 1:25000 соответствует четыре листа карты масштаба 1:10000, которые обозначают арабскими цифрами 1, 2, 3, 4. Номенклатура последнего листа карты М 1:10000 – N – 37 – 144 – Г – г – 4.

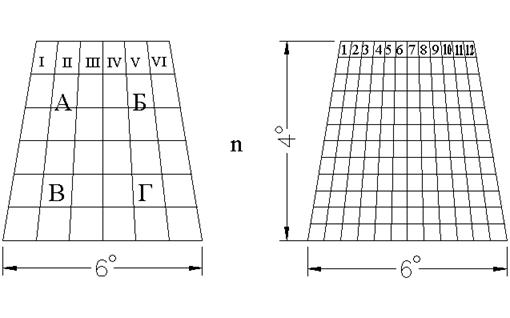Рис.4.4. Разграфка топографических планов

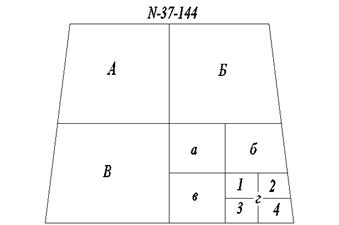	Лист карты масштаба 1:100000 служит основой для разграфки и номенклатуры более крупных масштабов. Одному листу карты масштаба 1:100000 соответствует 256 листов карты М 1: 5000, которые обозначают арабскими цифрами от 1 до 256, например –N – 37 – 144-(256).
Рис.4.5. Номенклатура листов карт

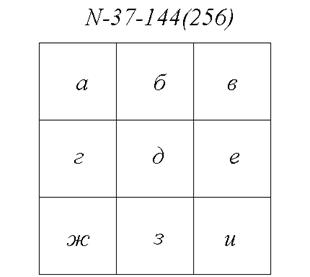	Одному листу масштаба 1:5000 соответствует девять листов масштаба 1:2000, которые обозначают буквами русского алфавита а, б, в, г, д, е, ж, з, и (Рис. 4.6), написанными в скобках справа от номенклатуры М 1:5000. Номенклатура последнего листа М 1:2000 – N –37- 144- (256 –и).
Рис.4.6.

В пределах листа карты М 1: 5000 и крупнее искажений за кривизну Земли практически нет, поэтому изображение местности на таком листе представляет собою план на горизонтальной плоскости.

Инструкцией по топо-геодезическим работам для городского, поселкового и промышленного строительства от 1992 г. разрешается съемка и составление планов в масштабах 1:5000 – 1:500 на планшетах квадратной или прямоугольной разграфки. За основу принимается планшет масштаб 1: 5000 с размерами 40 х 40 см (2 х 2 км, 400 га).

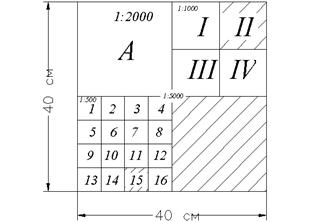	Одному листу плана М 1:5000 ( Рис. 4.7) соответствует четыре листа М 1: 2000 (А, Б, В, Г). Одному листу плана 1:2000 соответствует четыре листа М 1: 1000 (I , II, III и IV) и 16 листов 1:500, которые нумеруют арабскими цифрами от 1 до 16.
Рис.4.7.

4.5. Использование топографических карт и планов в архитектурно - планировочном проектировании.

Топографические карты и планы являются основным исходным материалом на всех этапах архитектурно-планировочного проектирования. Они позволяют оценить природные особенности района: качество земель для предполагаемого строительства, их расположение по отношению к ядру населенного места или района, условия рельефа, залесенность, климатические особенности, наличие инфраструктуры и т.д. Решая различные задачи на картах и планах можно получить координаты объектов, расстояния, размеры, уклоны на выбранных участках и другие параметры, нахождение которых в реальных условиях представляет обычно трудоемкую задачу.

На каждом этапе проектирования используются различные по масштабам и точности карты и планы.

При решении задач по проектированию обширных территориальных систем или районов, используются карты масштабов 1:500000 – 1: 100000, для комплексной оценки территорий и разработки схематичных генпланов карты масштабов 1:50000-1:25000, для разработки генеральных планов городов используются планы масштабов 1: 5000 (для крупных городов), 1: 2000 для мелких городов и разработки проектов вертикальной планировки, составления разбивочных чертежей с привязкой к красным линиям или геодезическим пунктам. Топографические планы масштаба 1: 1000 используют для разработки технических проектов и рабочих чертежей, а 1:500 является основным масштабом для составления исполнительных генеральных планов застроенной территории.

4.6.Способы измерения площадей на планах и картах.

Существуют следующие основные способы измерения площадей: аналитический, графический и механический.

Аналитический способ

Площадь многоугольника S вычисляют по координатам вершин полигона, используя формулы :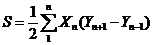

и для контроля

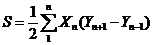
где n - номера вершин полигона. Этот способ наиболее точный. Пример вычисления площади пятиугольника ( Рис. 4.8) приведен в таблице 4.2

Таблица 4.2

X	У	yn+1 - yn-1	xn-1 - xn+1	xn( yn+1 - yn-1)	yn(xn-1 - xn+1)
X1	У1	y2 – y5	x5 – x2	X1(y2 – y5)	У1(x5 – x2)
X2	У2	y3 – y1	x1 – x3	X2(y3 – y1)	У2(x1 – x3)
X3	У3	y4 – y2	x2 – x4	X3(y4 – y2)	У3(x2 – x4)
X4	У4	y5 – y3	x3 – x5	X4(y5 – y3)	У4(x3 – x5)
X5	У5	y1 – y4	x4 – x1	X5(y1 – y4)	У5(x4 – x1)
				Σ1n = 2S	Σ1n = 2S

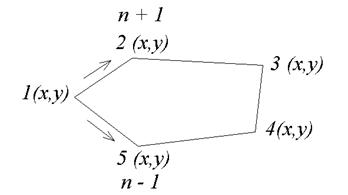Рис.4.8. Аналитический способ

Графический способ.

а) Определение площади при помощи палетки. Точность этого способа 1/50 к площади определенной аналитическим путем. Палетка – это сетка квадратов, нанесенная на прозрачной основе.

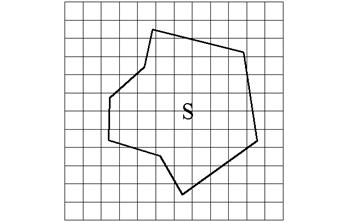	Палетку накладывают на контур (Рис. 4.9), площадь которого определяют как количество полных и неполных квадратов (дополняя их до полных). Площадь S определяют по формуле S = f n, где f - площадь одного квадрата с учетом масштаба плана, n – число квадратов.
Рис.4.9. Графический способ

б) Способ геометрических фигур. Участок, площадь которого определяют, разделяют на фигуры, площадь которых можно определить по формулам геометрии (треугольники, трапеции и др.). Измеряют основание,высоту и вычисляют площадь с точностью 1/100 к площади определенной аналитическим способом.

в) Механический способ. Площадь определяют с помощью планиметра. Точность этого способа от 1/200 до 1/400 к площади, определенной аналитическим методом.

Планиметр состоит из двух рычагов – полюсного и обводного. Полюсный рычаг на одном конце имеет груз с иглой накалываемой на бумагу, а на другом конце - штифт с круглой головкой, вставляемой во втулку обводного рычага.

Обводной рычаг представляет собой металлическую линейку с миллиметровыми делениями. На одном конце рычага имеется обводной шпиль (или стеклышко с точкой посредине) и ручка. На обводном рычаге имеется каретка со счетным механизмом, которую можно перемещать вдоль рычага и зажать в определенном положении. Это положение можно зафиксировать отсчетом по верньеру на каретке механизма.

На рисунке 4.10 показан отсчет по счетному механизму планиметра. Этот отсчет равен 4558. Для определения площади участка, обводной шпиль ставят в любую точку на контуре, а полюс- вне контура (между рычагами в начальном положении угол должен быть близким к 90⁰) и берут отсчет по счетному механизму n₁, например 4558.

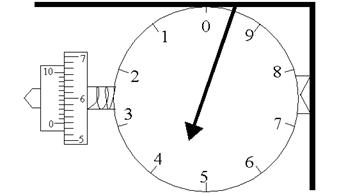	Затем ведут обводной шпиль по контуру фигуры вправо по ходу часовой стрелки и возвращаются в исходную точку, где снова берут отсчет n2, например 6769. Вычитая из второго отсчета первый получают площадь обведенной фигуры в делениях планиметра S = n2 - n1 = 6769 –4558 =2211
Рис.4.10. Планиметр

Для получения площади этой фигуры в квадратных метрах необходимо полученную площадь в делениях планиметра умножить на цену деления планиметра - С, тогда S = с(n₂ -n₁).

При определении площади с полюсом внутри контура фомула будет иметь такой вид.

S = с(n₂ -n₁+ Q), где Q – постоянное число планиметра.

Для определения цены деления планиметра с вычерчивают в данном масштабе квадрат. Вычисляют его площадь с учетом масштаба. Так, например, масштаб плана 1:1000, а сторона квадрата 10 см, тогда площадь его на местности равна 10000 м². Определив площадь его в делениях планиметра при обводе с полюсом вне контура, вычисляют цену деления.

C = S _{В КВ. М} / S _{В ДЕЛ. ПЛАН.} = 10000 м² / 1000 = 10 м²

Для большей уверенности разностиn₂ -n₁ получают несколько раз и если они не отличаются более чем на 4-5 делений, то берут среднее из них.

Таблица 4.3.

Отсчеты	Разности отсчетов	Средние разности отсчетов
n3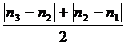
n2	n3 – n2
n1	n2 – n1

Для определения постоянного числа планиметра Q обводим площадь какой-либо фигуры с полюсом вне фигуры и получаем первую разность отсчетов n₂ -n_{1 .} Потом устанавливаем полюс внутри той же фигуры и после обвода получаем вторую разность отсчетов n₂^I -n₁^I.Вычитая из первой разности вторую получаем q в делениях планиметра q = (n₁ – n₂) - (n₁^I – n₂^I), а значение Q определяем по формуле Q = сq.

4.7. Решение задач на топографических картах и планах.

При разработке проектов планировки и застройки населенных пунктов на картах и планах могут решаться следующие задачи:

· определение географических координат точек;

· определение прямоугольных координат точек;

· определение длин линий;

· определение ориентирных углов;

· определение высот точек;

· определение крутизны скатов;

· построение профиля местности по заданному направлению;

· проектирование по карте горизонтальных и наклонных площадок.