Построение теней в перспективе
При построении теней на перспективных чертежах за источник света принимается солнце, которое по отношению к картине может занимать различные положения:
1. солнце расположено позади предмета и тень падает в сторону наблюдателя (рис. 104);
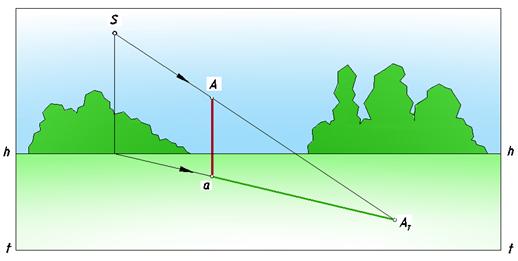
Рис. 104. Солнце позади предмета
2. солнце расположено позади зрителя, тень падает в сторону линии горизонта от основания предмета (рис. 105);
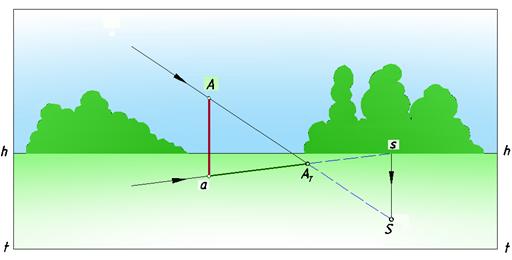
Рис. 105. Солнце позади зрителя
3. солнце расположено сбоку так, что лучи идут параллельно картине (рис. 106).
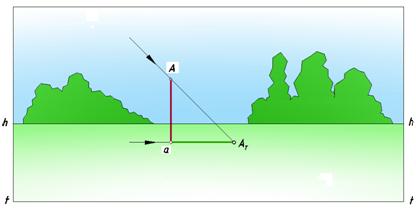
Рис. 106. Солнце сбоку предмета
Последний случай чаще других применяется инженерами при построении перспективных изображениях зданий и сооружений, поэтому остановимся на нем более подробно.
Рассмотрим построение точки в перспективе. Будем считать, что объект освещается слева (или справа), лучи идут параллельно картине, составляя угол 45° с предметной плоскостью. Запишем эти условия символически:
1. S ∥K;
2. S^T = 45°.
Проведем через точку A (рис. 107) перспективу луча, а через ее вторичную проекцию (точку a) – вторичную проекцию луча. Поскольку луч параллелен картине, его вторичная проекция параллельна основанию картины t – t. Точка пересечения перспективы луча с его вторичной проекцией определит действительную тень точки А на земле – точку АТ.
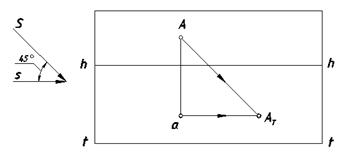
Рис. 107. Тень точки в перспективе
Построим собственные и падающие тени параллелепипеда, стоящего на земле (рис. 108).
Заметим, что те выводы, которые были сформулированы ранее для построения теней в ортогональных проекциях, справедливы и для центральных.
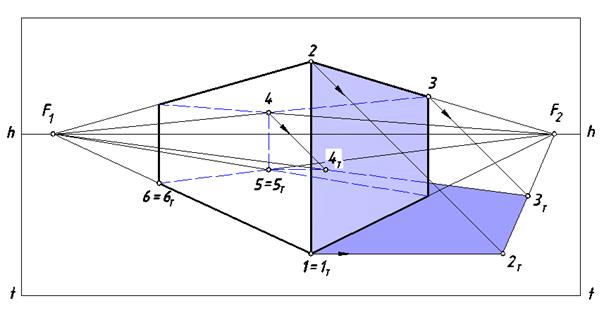
Рис. 108. Построение теней параллелепипеда
Проанализируем освещенность граней параллелепипеда. При заданном направлении лучевого потока освещенными будут верхняя, левая видимая и невидимая на чертеже грани объекта. Остальные грани окажутся в собственной тени. Определим контур собственной тени данного тела. В его состав войдут ребра [12] – [23] – [34] – [45] – [56] – [61], составляющие замкнутую цепочку в виде пространственной ломаной линии. От выявленного контура строим падающую тень. Поскольку точка 1 лежит на земле 1 = 1Т. Проведем через точку 2 перспективу луча, а через ее вторичную проекцию (точку 1) – его вторичную проекцию. На пересечении этих линий находим точку 2Т. Поскольку ребро [23] параллельно предметной плоскости, его падающая тень равна и параллельна ему. Точка схода ребра [23] находится на линии горизонта (точка F1). Соединяем точку 2Т с этой точкой (т.е. проводим через нее прямую, параллельную этому ребру). На этой же прямой находится тень точки 3. Проведем через точку 3 перспективу луча до пересечения с построенной прямой – определим точку 3Т.Вторичную проекцию луча в этом случае строить не следует, поскольку искомая точка уже установлена пересечением двух линий. Ребро [34] также параллельно плоскости T, его тень параллельна ребру.
Точкой схода этих прямых – фокус F1. Проведя перспективу луча через точку 4 до пересечения с отрезком [3Т F1], определим точку 4Т. Точки 5 и 6 расположены на предметной плоскости T, поэтому 5 = 5Т и 6 = 6Т. Очертание контура падающей тени параллелепипеда состоит из совокупности отрезков [1Т 2T] – [2Т 3T] – [3Т 4T] – [4Т 5T] – [5Т 6T] – [3Т 4T], представляющих собой замкнутый контур.
Рассмотрим задачи, связанные с построением перспективы и теней фрагментов зданий
З а д а ч а 1
Построить тени от прямых барьеров на лестнице, земле и стене
(рис. 109).
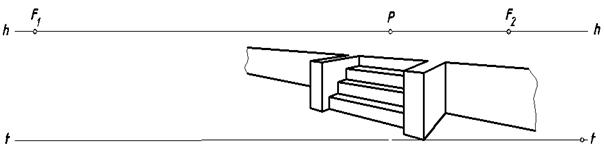
Рис. 109. Лестница с прямыми барьерами
Вначале построим тени правого барьера (рис. 110). Поскольку при заданном направлении светового потока правая грань барьера находится
в собственной тени легко видеть, что ребра, находящиеся на границе света и тени войдут в состав контура собственной тени. Определим падающую тень вертикального ребра. Точка А принадлежит Т, поэтомуможно отметить, что А = АТ. Проведем через точку В перспективу луча, а через ее вторичную проекцию – точку А перспективу вторичной проекции луча. На пересечении построенных линий определим тень ВТ.Другое ребро [BC] параллельно предметной плоскости, следовательно, его тень параллельна ребру и имеет ту же точку схода F2. Реальная часть этой тени на земле – отрезок [ВТ1Т]. Поскольку точка 1Т находится на границе земли и стены
1Т = 1Т'. С помощью обратного луча можно определить точку на ребре [BC], которая отбросила эту тень. Точка С горизонтального ребра находится на стене, поэтому С = СТ'. Тень отрезка [1C] падает на стену. Его тенью является отрезок [1Т' СТ' ].
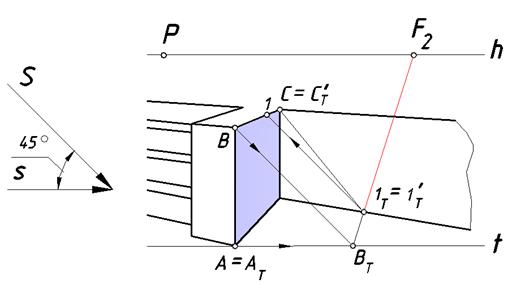
Рис. 110. Построение контура падающей тени правого барьера
Контур собственной тени всегда замкнут. Рассуждения по его определению приводились во многих задачах. Элемент контура может совпадать со своей тенью (если, например, он находится на земле, стене или примыкает к другому объекту). Этот фактор следует учитывать при построении падающей тени.
У левого барьера правая грань находится в собственной тени, следовательно, ребра [LN] и [LM] входят в состав определяемого контура
(рис. 111). Построим падающие тени этих ребер.
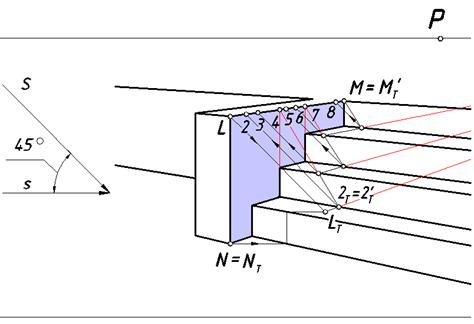
Рис. 111. Построение контура падающей тени левого барьера
Лучевая плоскость (фронтальная плоскость уровня), проходящая через ребро [LN] пересекает землю и нижнюю ступеньку по параллельным прямым, оставляя на них теневые следы, а подступенок по вертикальной прямой. Верхняя точка L этого ребра отбрасывает тень на первую ступеньку и определяется пересечением луча с его вторичной проекцией. Ребро [LM] параллельно плоскости нижней ступеньки, поэтому его тень параллельна ребру. Соединяет точку LТ с точкой схода F2 и отмечаем реальную часть тени этого ребра на нижней ступеньке до точки 2Т = 2Т'. Заметим, что это ребро является гвоздем по отношению ко всем подступенкам. Проведем вспомогательные линии для нахождения общих точек для ребра [LM] и граней всех подступенков. Эти построения позволят определить падающие тени на подступенки. На рис. 111 на ребре [LM] отмечены все его участки, отбросившие тени на конкретные фрагменты лестницы, землю
и стену.
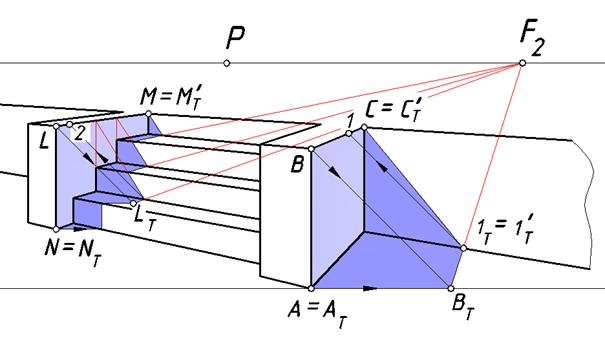
Рис. 112. Собственные и падающие тени от прямых барьеров
На рис. 112. представлен окончательный вариант решения задачи.
Тени ребер [LM] и [BC] на стене и подступенках параллельны
и представляют собой пример восходящих прямых. Их точка схода расположена выше линии горизонта, а точка схода их вторичных проекций лежит на линии горизонта.
З а д а ч а 2
Построить перспективу карниза крыши и определить собственные и падающие тени (рис. 113).
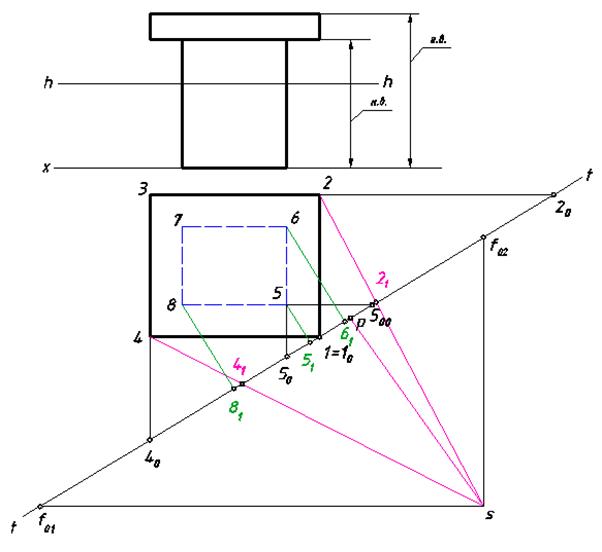
Рис. 113. Условие задачи 2
Укажем на ортогональном чертеже условия задачи положение картинной плоскости и выберем точку зрения в соответствии с рекомендациями, приведенными ранее.
Для решения задачи применим способ архитекторов и используем некоторые другие приемы построения перспективы. Определим начальные точки прямых доминирующих направлений и отметим их на перспективном чертеже на основании картины. Определим точки схода этих прямых.
Соединив начальные точки с соответствующими точками схода, получим перспективу плоской фигуры (плана карниза крыши). Проведем через точку зрения и точки 2 и 4 лучи, которые вместе с их вторичными проекциями задают горизонтально-проецирующие плоскости, пересекающие картину по вертикальным прямым (рис. 114).
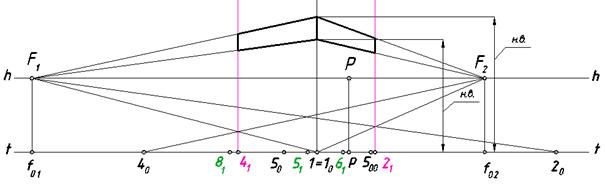
Рис. 114. Применение двух методов построения перспективы
В соответствии с этими рассуждениями наперспективном чертеже
проведем через точки 21 и 41 вертикальные прямые, по которым пересекутся построенные плоскости с картиной. Ребро, попавшее в картинную плоскость, изобразится на ней в натуральную величину, взятую с ортогонального чертежа. Проведя через верхнюю и нижнюю точки этого ребра прямые в точки схода F1 и F2, завершим построение двух боковых видимых граней карниза (рис. 115).
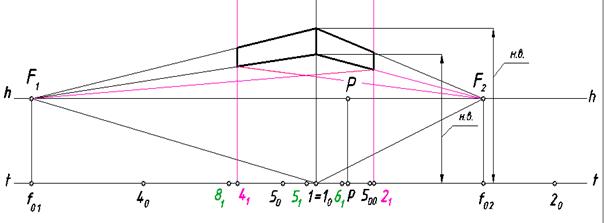
Рис. 115. Построение боковых граней карниза
с использованием способа конических сечений
Проведем две прямые через нижние точки вертикальных боковых ребер карниза в точки схода F1 и F2, и выделим очертание нижней грани (рис.116).
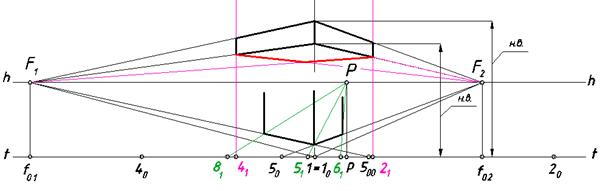
Рис. 116. Проведение прямых, перпендикулярных картине
Для построения перспективы стен использованы прямые, перпендикулярные картине, проходящие через точки 5, 6 и 8.
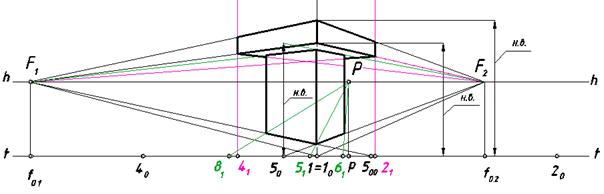
Рис. 117. Построение видимых стен в перспективе
После нахождения вторичных проекций этих точек на перспективном чертеже проводим через них вертикальные линии (рис. 116).
Сдвинем одно из вертикальных ребер в картинную плоскость в любом направлении. Отложим на нем от основания картины от точки 50 натуральную величину ребра, взятую с ортогонального чертежа (рис. 117).
Проведем через верхнюю точку этого ребра прямую в точку схода F2. Обведем очертание правой стены. Затем построим параллельные прямые с точкой схода F1 и обрисуем левую стену.
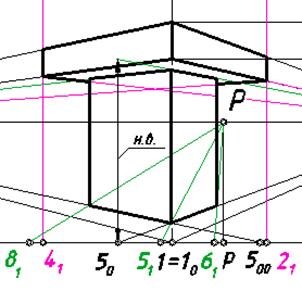
Рис. 118. Завершающий этап построения перспективы
На рис.118. показан окончательный результат построения перспективы сооружения.
Перейдем к построению теней. Определим освещенность граней объекта при заданном направлении светового потока и выделим его собственные тени. Построим падающую тень карниза крыши на стены. Найдем тень точки А на левой видимой стене. Проведем через точку А перспективу луча, а через а вторичную проекцию до пересечения с левой стеной. Заметим, что луч и ребро представляют собой скрещивающиеся линии. Пересечение проведенного луча со стеной произойдет в точке АТ'. Поскольку нижнее переднее ребро левой грани карниза параллельно левой стене, то тень от него пойдет по стене вправо от точки АТ' параллельно этому ребру. Поэтому через АТ' и точку схода F1 проводим прямую.
В точке А сходятся три ребра карниза. Его левое нижнее ребро является гвоздем по отношению к левой стене. Определим тень этого ребра. На рис. 119 показано два варианта нахождения тени.
В первом случае (рис. 119, а) на этом ребре строим с помощью обратного луча точку В, которая отбросит тень ВТ' на левое вертикальное ребро. Тенью гвоздя является отрезок [АТ' ВТ' ].
Во втором случае (рис. 119, б) найдена общая точка для левой стены гвоздя. Для этого верхнее горизонтальное ребро левой стены продолжено до пересечения с гвоздем и отмечена точка СТ'. Поскольку отрезок [СТ' АТ' ] лежит в плоскости стены и пересекает ее левое вертикальное ребро, на нем можно отметить точку ВТ' и выделить реальную часть тени гвоздя.
Оба приема дают одинаковый результат.
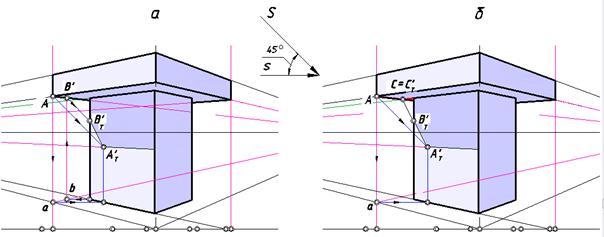
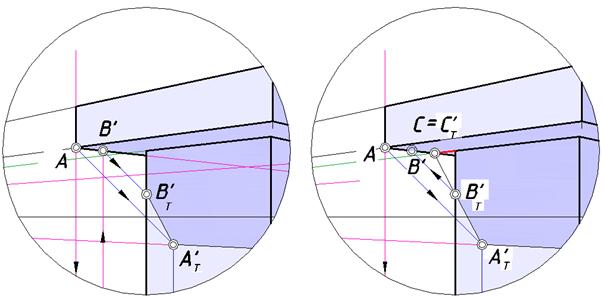
Рис. 119. Варианты нахождения падающей тени карниза
на стену здания:
а – с помощью точки BТ' ;
б – с помощью точки СТ' («основания» гвоздя на стене)
На рис. 120 приведена перспектива этого сооружения при выборе другой точкой зрения, при которой тень точки А падает на невидимую на картине стену. По отношению к этой стене ребро [АВ] является гвоздем
и частично отбрасывает на нее тень в виде отрезка [СТ' АТ' ]. На левой стене построена тень нижнего ребра видимой левой грани карниза.
Построение теней карниза на фрагменты сооружения выполнено
в различных вариантах, поскольку вызывает трудности у студентов при выполнении работ.
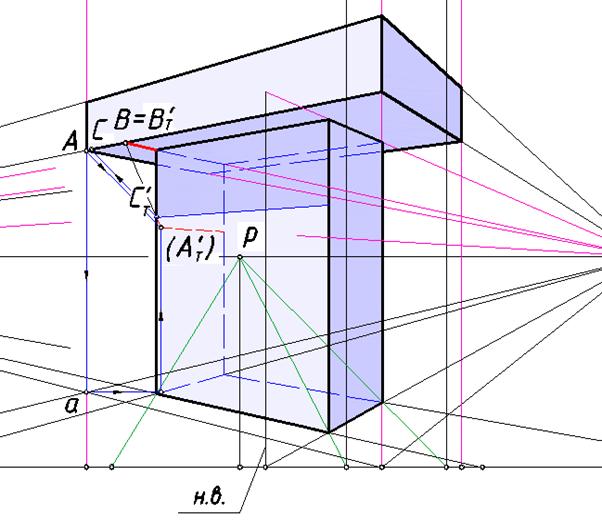
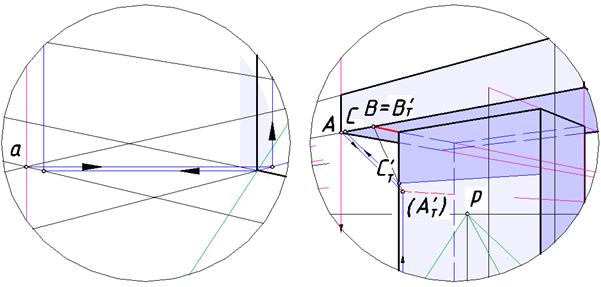
Рис. 120. Построение тени карниза при измененной точке зрения
Построим падающую тень карниза на землю отдельно от нижней части сооружения (рис. 121), предварительно определив его контур собственной тени.
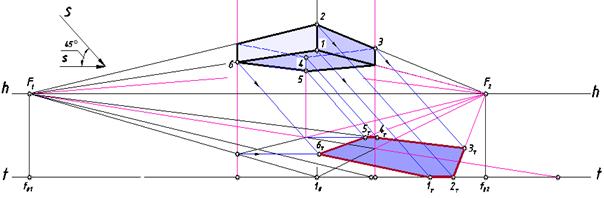
М 2:1
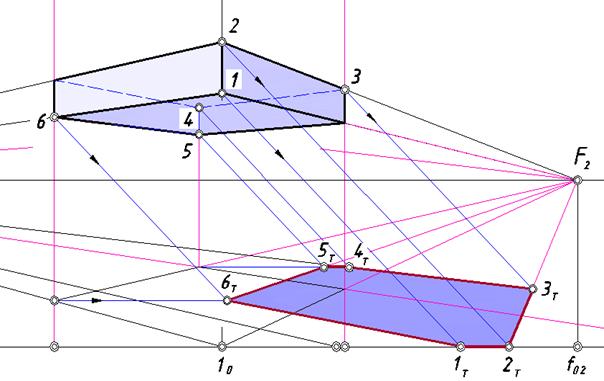
Рис. 121. Падающая тень карниза
Затем найдем контур собственной тени и определим контур падающей тени здания без учета карниза (рис. 122).
Обрисуем очертание общего контура падающей тени сооружения
и выделим его цветом (рис. 123).
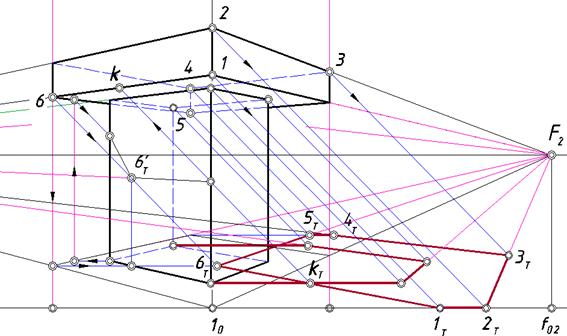
Рис. 122. Контуры падающих теней двух объектов
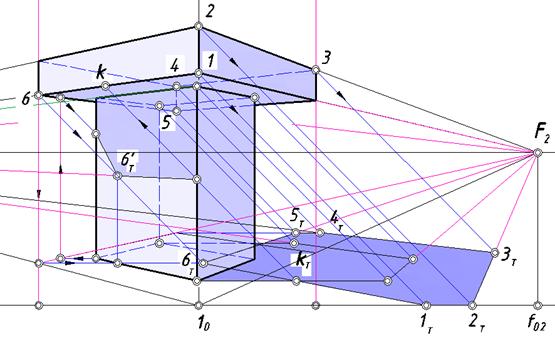
Рис. 123. Собственные и падающие тени объекта
Цвет падающей тени зависит от объекта, на котором она оказалась (на траве, асфальте и т. п.) и имеет более густой оттенок по сравнению
с собственной тенью, как показано ни рисунке выше.
З а д а ч а 3
По заданным видам здания выполнить вид слева и построить собственные и падающие тени (рис.124).
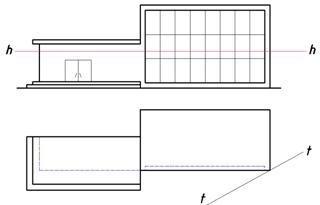
Рис. 124. Условие к задаче 3
Покажем на плане здания положение картинной плоскости, точку зрения, точки схода параллельных прямых двух направлений и проведем вспомогательные прямые для построения перспективы (рис.125).
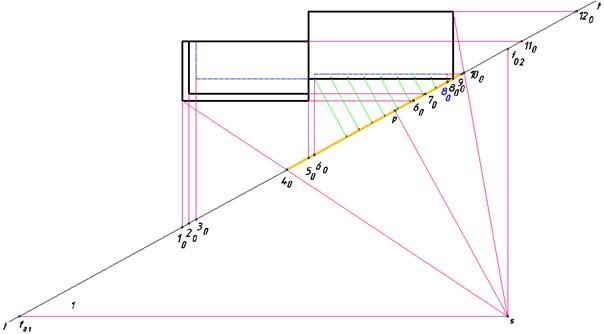
Рис. 125. Выбор картины и точки зрения на плане здания
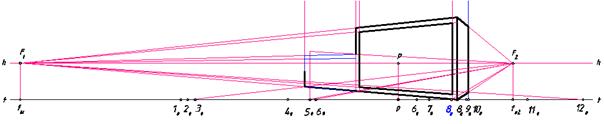
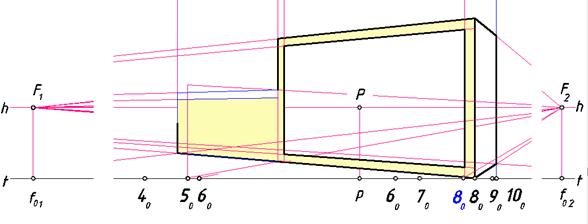
Рис. 126. Перспектива видимых стен здания
Нанесем на основании картины начальные точки прямых. Построим перспективу видимых стен здания (рис. 126).
Сформируем нишу в стене фасада. Фрагменты ниши с линиями построения показаны на рис. 127.
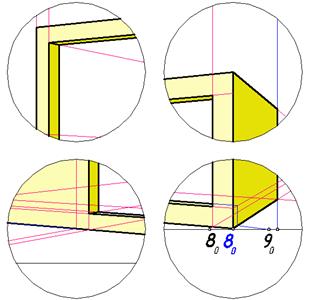
Рис. 127. Перспективы фрагментов ниши
На ребре, лежащем в картинной плоскости, нанесем точки деления для построения окон и соединим их с точкой схода F1. Для построения вертикальных линий используем прямые, перпендикулярные к картине,
с точкой схода P (рис.128).
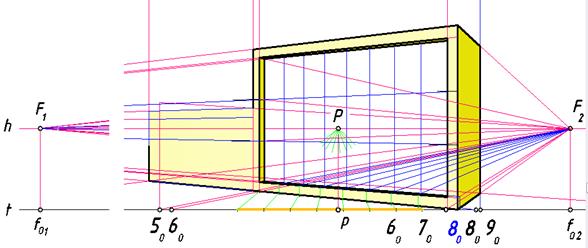
Рис. 128. Формирование окон в перспективе
Через точки деления на нижней грани ниши проведены параллельные прямые с точкой схода F2. На задней грани ниши построены вертикальные прямые и обрисованы оконные отсеки (рис. 129).
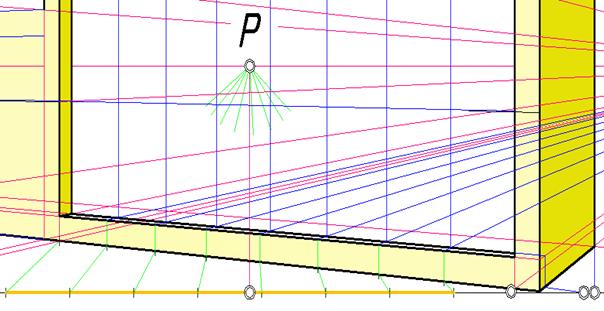
Рис. 129. Фрагмент обрисовки окон
По нанесенным на плане линиям начинаем построение ступенек (рис. 130).
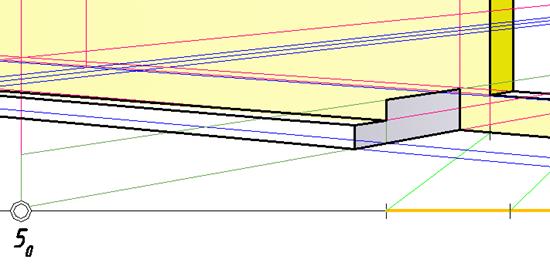
Рис. 130. Начало построения ступенек
По натуральным величинам вертикальных отрезков на картинной плоскости выполняем очертание профиля ступенек и правой части козырька (рис. 131).
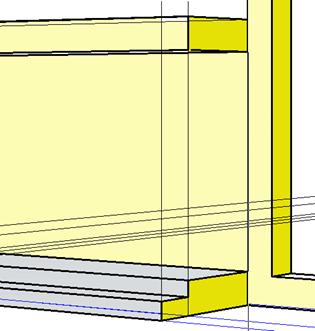
Рис. 131. Построение профиля ступенек и части козырька
Строим левую часть лестницы и козырька (рис. 132).
Рис. 132. Построение левого фрагмента здания
На рис. 133. показан увеличенный фрагмент части козырька, на котором видна грань, находящаяся в собственной тени,
Рис. 133. Левая часть козырька
В приведенных выше рисунках на изображениях показывались собственные тени для полноценного восприятия чертежа. Объяснений по поводу их построений не приводилось, поскольку ранее было рассмотрено на эту тему достаточное количество задач.
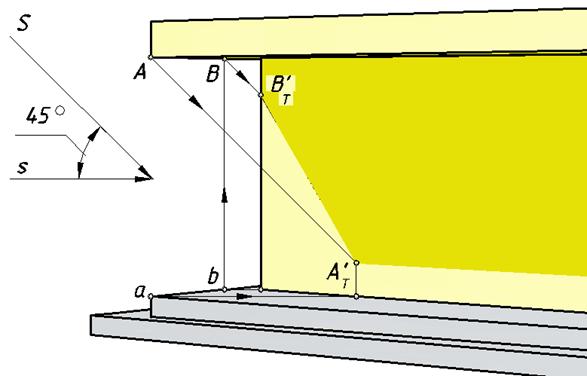
Рис. 134. Построение падающей тени козырька на стену здания
Падающие тени козырька (рис.134) следует строить от тех ребер, которые находятся на границе света и тени. Эту границу (контур собственной тени) хорошо видно на рис. 135.
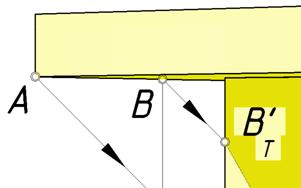
Рис. 135. Фрагмент козырька с собственной и падающей тенями
Элементами этого контура являются нижнее переднее ребро козырька, параллельное стене, и левое нижнее ребро, перпендикулярное стене. Точка А является общей для этих ребер. Для нахождения тени через нее проводим луч и строим его вторичную проекцию. Пересечение луча со стеной произойдет в точке АТ'. Проводим через эту точку прямую в точку схода F1. С помощью обратного луча определяем точку В на ребре, перпендикулярном стене, которая отбросит тень на левое ребро стены. Отрезок [АТ' ВТ' ] – падающая тень гвоздя на стене.
На рис. 136 видно, что ребра профиля лестницы, параллельные земле, и их тени имеют общую точку схода F2, ребро [45] частично отбрасывает тень на стену, начиная от точки 6, найденной с помощью обратного луча.
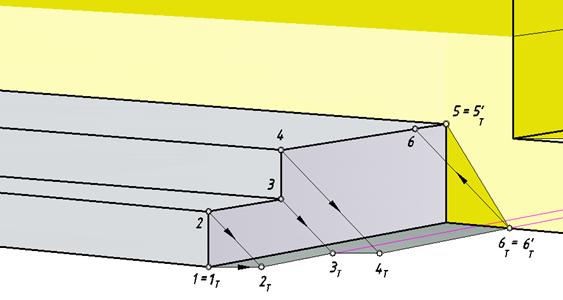
Рис. 136. Падающие тени от ступенек на земле и стене
Для нахождения тени козырька в нише можно поступить следующим образом. Вначале построить полное очертание падающей тени на стене без учета ниши (рис. 137). Определим тень точки А на плоскости стены (точку А1Т'). Соединим построенную точку с ВТ' и изобразим реальную часть тени гвоздя на стене. Сместив точку А1Т' вглубь ниши до совпадения с ее задней гранью найдем на ней тень точки А (точку А1Т' ).
Можно было провести построения в обратном порядке. Вначале определить тень точки А в нише окна (точку АТ' ). Затем найти в ней тени вертикального и горизонтального ребер.
На рис. 138 видна тень на подоконнике и на оконных стеклах от переднего вертикального ребра боковой грани ниши.
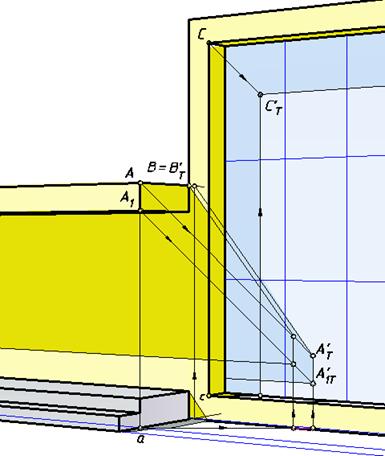
Рис. 137. Падающая тень козырька на стене и в нише
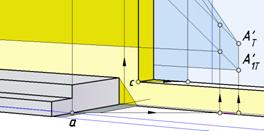
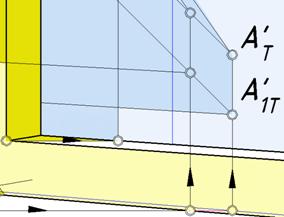
Рис. 138. Фрагмент построения падающей тени козырька
В правой части рис.138 видно, что вторичная проекция луча, проходящая через точку а, пересекает вторичную проекцию задней грани ниши. Через точку пересечения проведена вертикальная прямая, на которой отмечена точка АТ' .
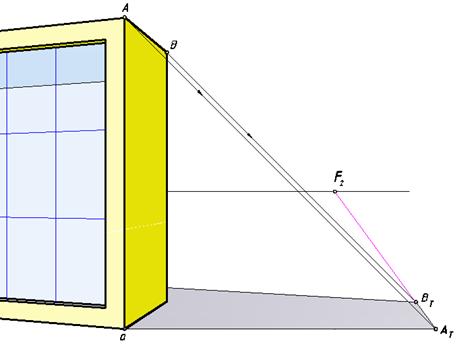
Рис. 139. Построение падающей тени здания на землю
При определении падающей тени здания (рис. 139) задействованы ребра, входящие в контур собственной тени. Это вертикальное ребро, находящееся в картинной плоскости, верхнее правое видимое ребро с точкой схода F2и верхнее невидимое ребро с точкой схода F1. Тени этих ребер на земле параллельны самим ребрам и имеют те же точки схода.
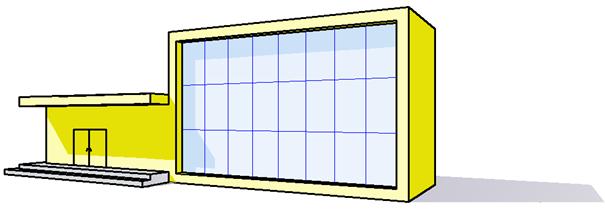
Рис. 140. Перспектива здания с собственными и падающими тенями
На завершенном изображении (рис. 140) показано, что падающие тени приобретают окраску той поверхности, на которую они отброшены, но тон окраски становится более густым.
Содержание заданий
1. Построить три ортогональные проекции схематизированного здания. Определить собственные и падающие тени здания. Выполнить отмывку на всех изображениях. Формат А3. Основная надпись форма 1.
2. Выполнить перспективу этого здания с построением собственных и падающих теней и отмывкой изображений. Формат А2. Основная надпись форма 1.


Рис. 141. Образец выполнения основной надписи по форме 1
Примечание
На рис. 141 приведены размеры основной надписи и пример ее заполнения
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Вольберг. О. А.Лекции по начертательной геометрии/ О. А.Вольберг. – Государственное учебно-педагогическое изд-во министерства просвещения РСФСР Москва – 1947 – Ленинград, – 348 с.
2. Зоммер Вернер. AutoCAD 2006 / Вернер Зоммер. – М. : изд-во БИНОМ, 2006. — 736 с.
3. Климухин А.Г. Начертательная геометрия / А.Г. Климухин. – М.: Стройиздат, 1978. – 336 с.
4. Кузнецов Н. С. Начертательная геометрия / Н.С. Кузнецов. – М.: Высш. Шк., 1981. – 264 с.
5. Короев Ю.И. Черчение для строителей / Ю.И. Короев. – М.: Высш. Шк., 1982. – 272 с.
6. Макарова М. Н. Перспектива / М. Н. Макарова. – М.: Академический проект, 2002. –512 с.
7. Сербина Е. И. Сборник задач по начертательной геометрии / Е. И. Сербина. – М.: Высш. Шк., 1970 –224 с.
8. Хватова Л. П. Начертательная геометрия, часть 2: метод. указания и контрольные работы / Л. П. Хватова и А. А. Родионова. — Свердловск : УПИ, 1974,–с.110
9. Пальшау А. Н. Начала начертательной геометрии /. А. Н. Пальшау. – Государственное технико-теоретическое изд-во Москва – 1939 – Ленинград, –
264 с.
10. Пеклич В. А. Начертательная геометрия / В. А. Пеклич.– М.: Изд-во АСВ, 2000. –248 с.
11. Четверухин Н. Ф. Начертательная геометрия / Н. Ф. Четверухин. – М.: Высш. Шк., 1963. – 420 с.
12. Шешко И. Б. Построение и перспектива рисунка /И. Б. Шешко. Минск, из-во «Вышейшая школа», 1973.– 128 с.
13. Яблонский А. Г.Начертательная геометрия (перспектива) / А. Г. Яблонский. – М.: из-во «Просвещение», 1966. – 176 с.
ПРИЛОЖЕНИЯ
1. Образец выполнения первого задания
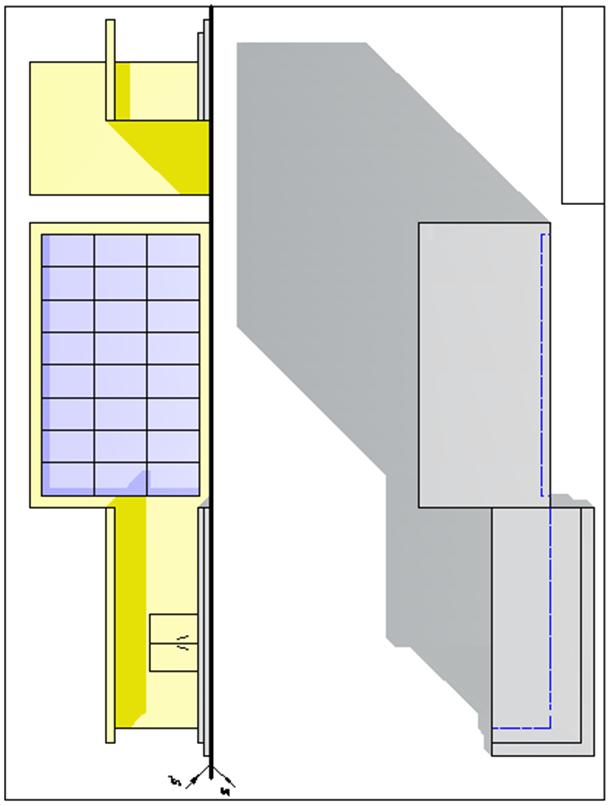
2. Образец выполнения второго задания
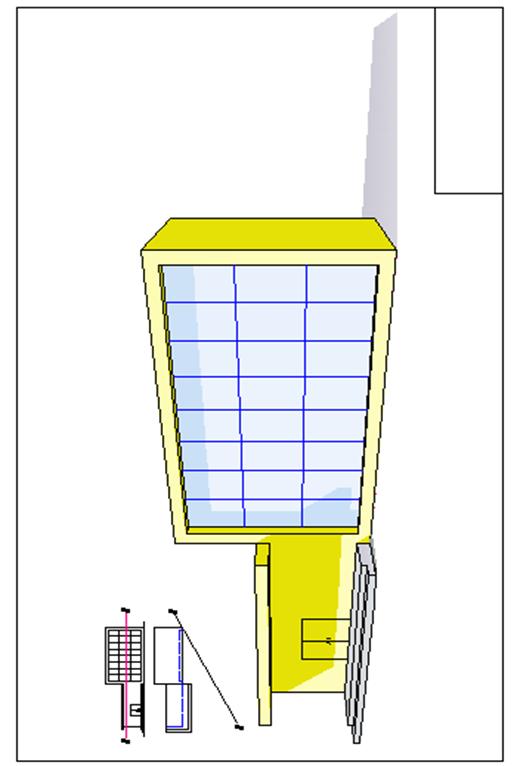
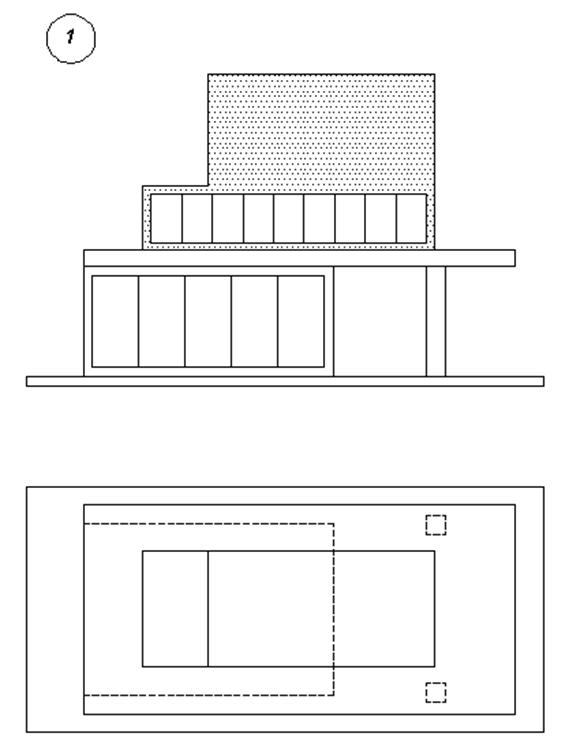
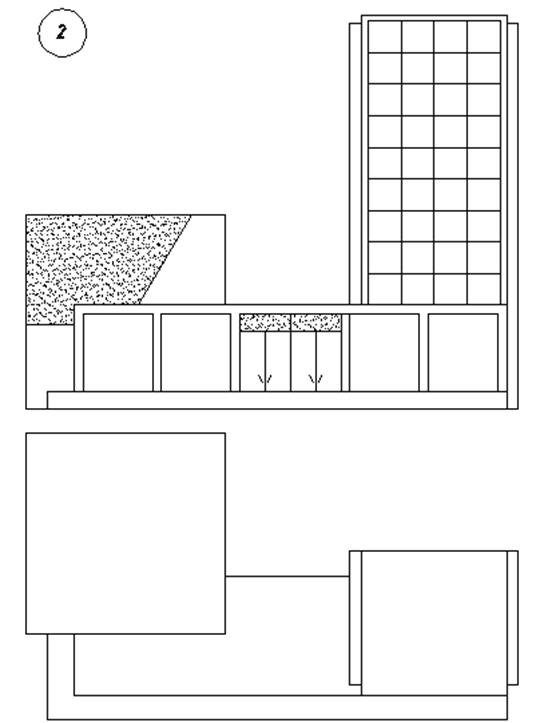
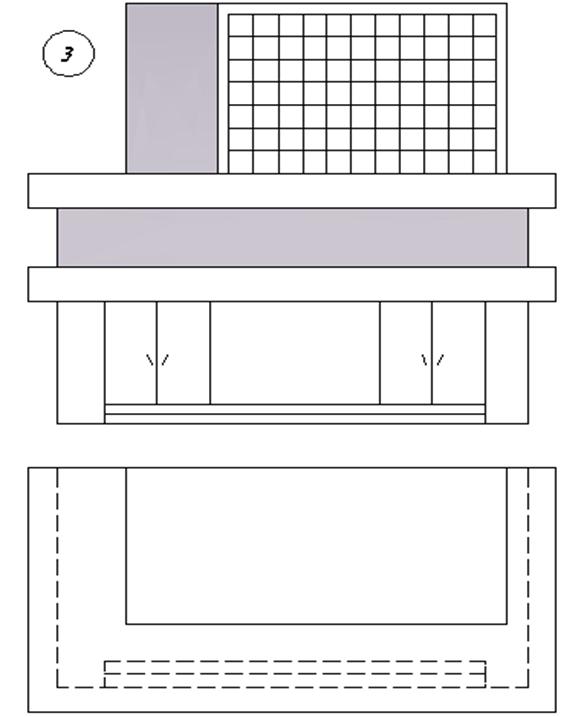
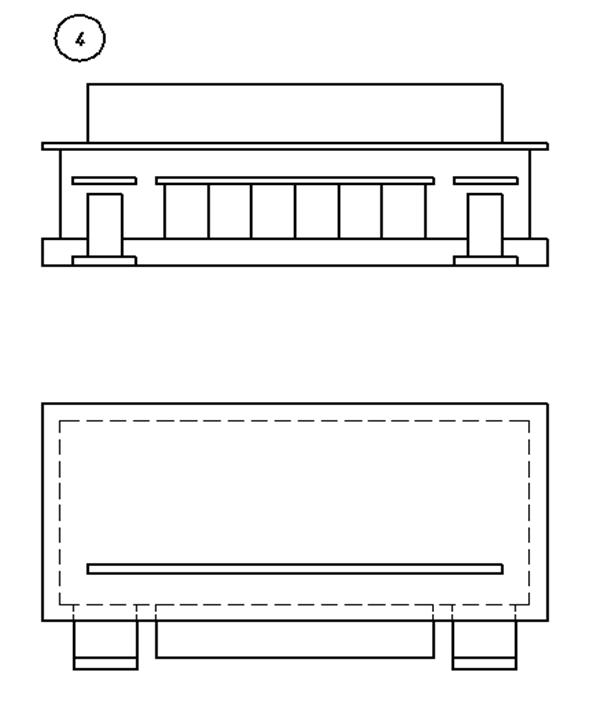
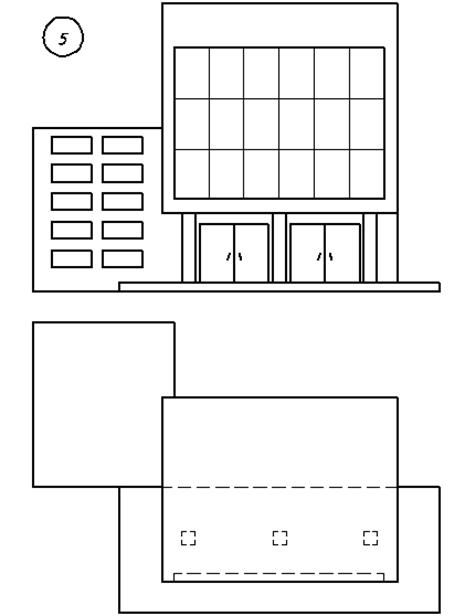
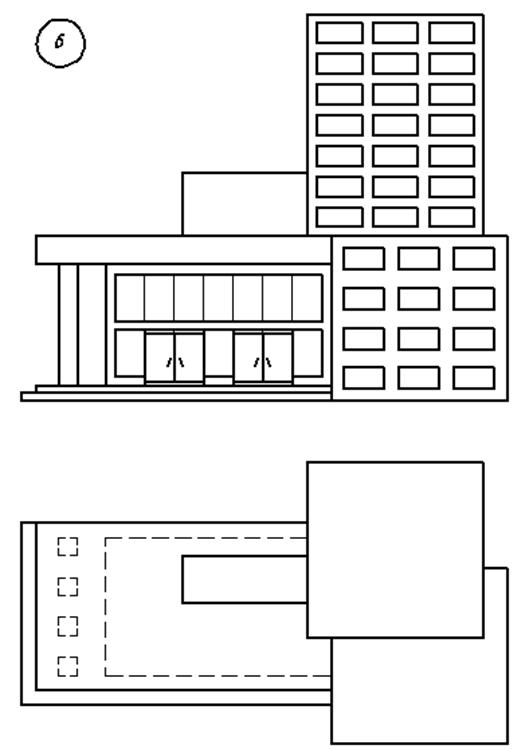
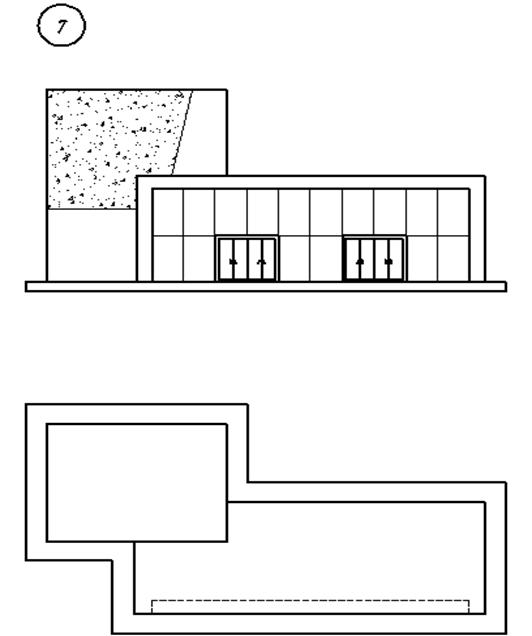
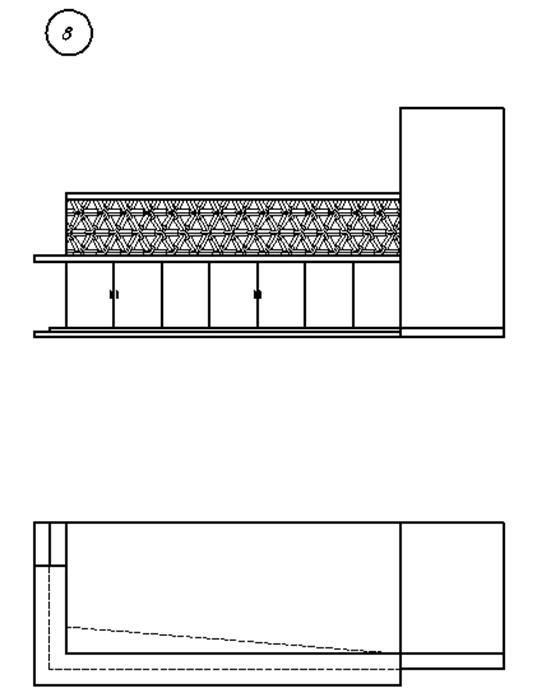
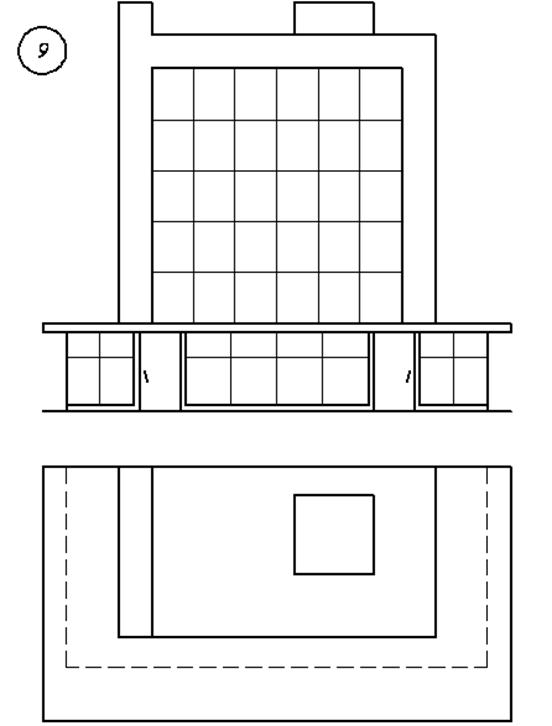
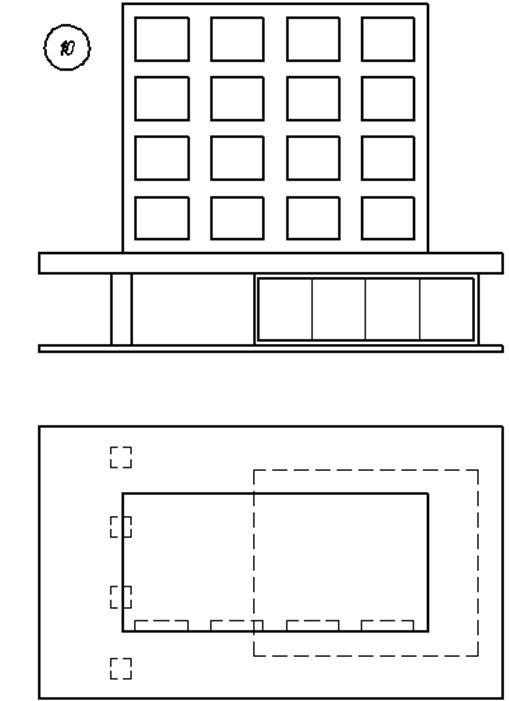
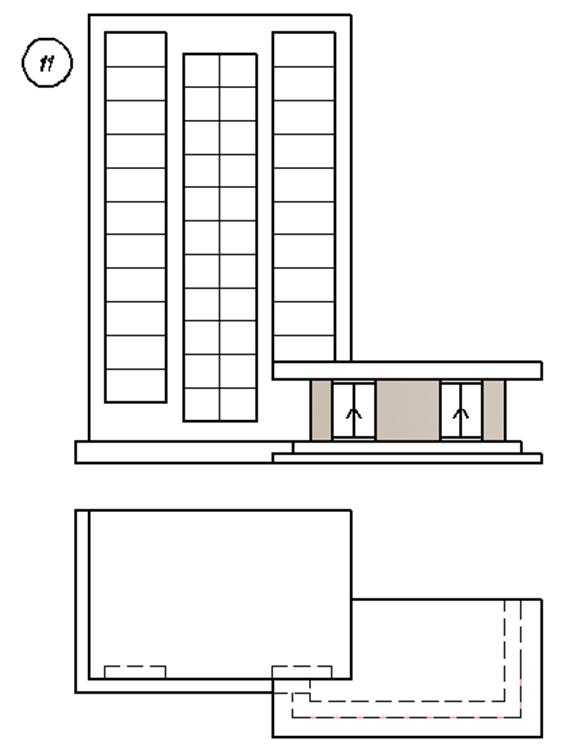
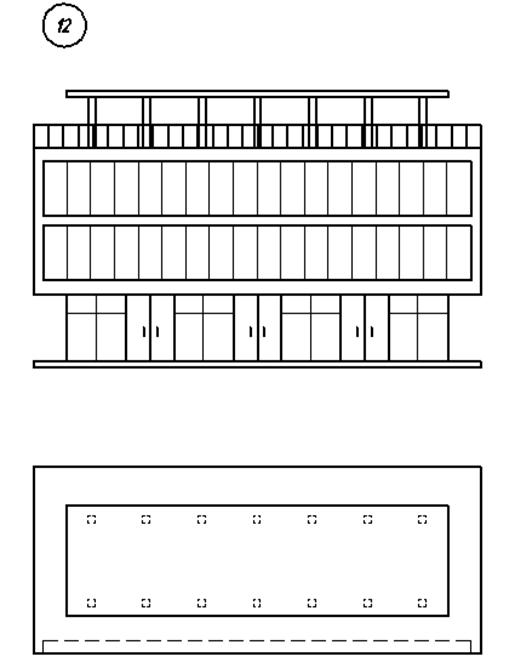
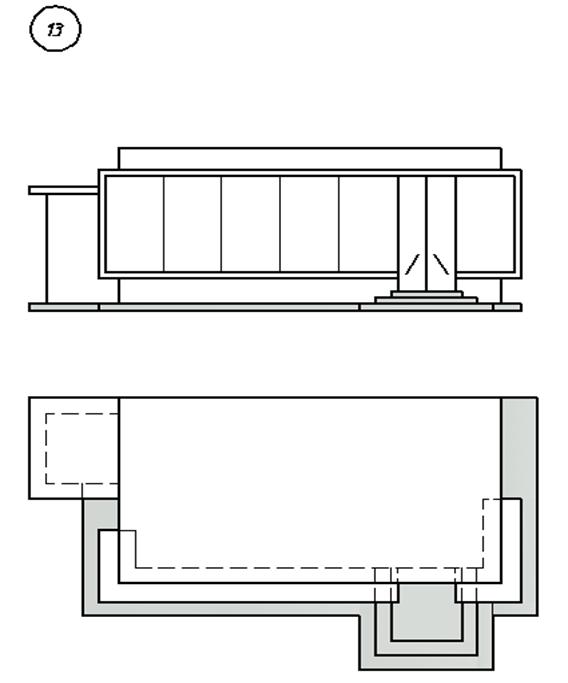
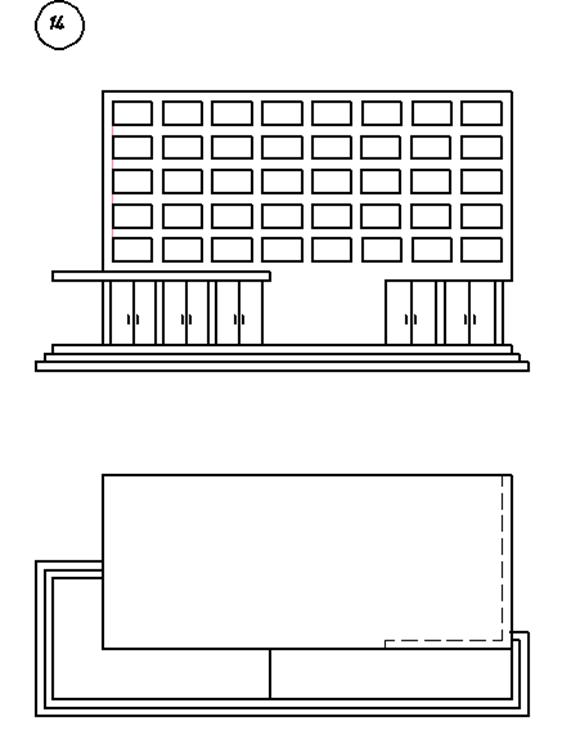
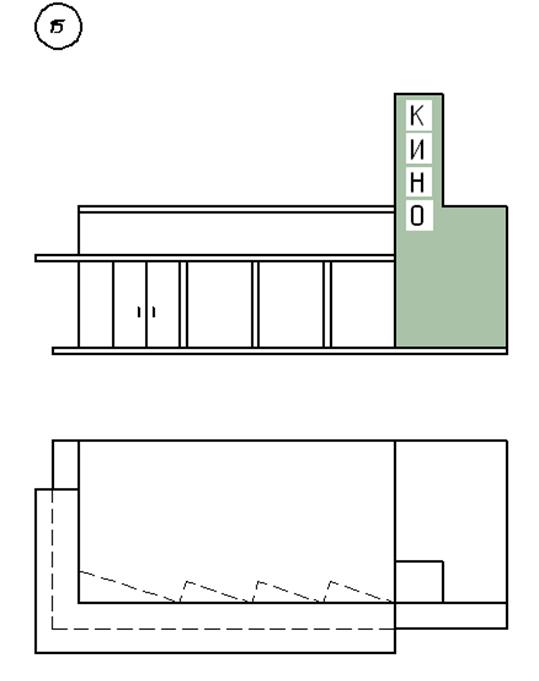
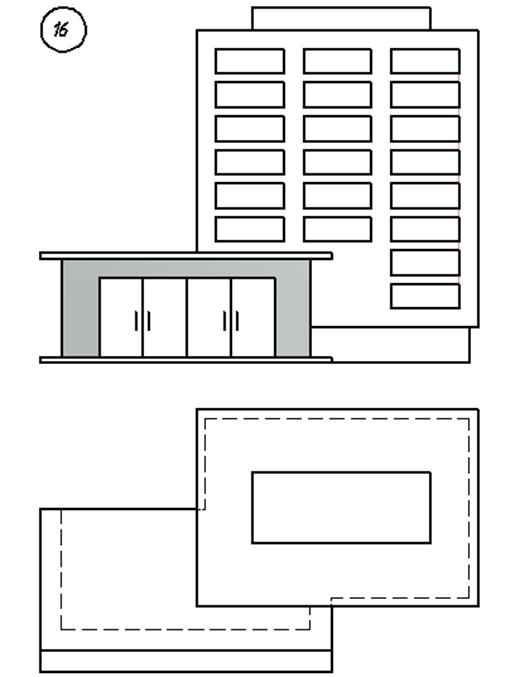
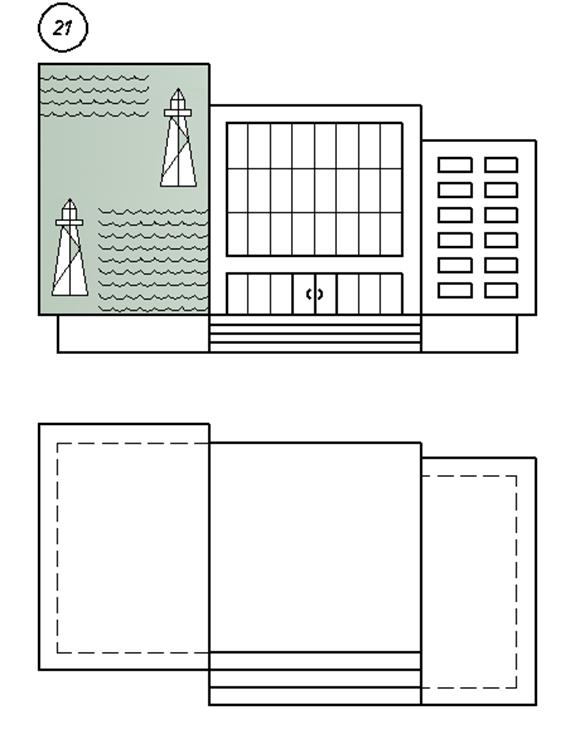
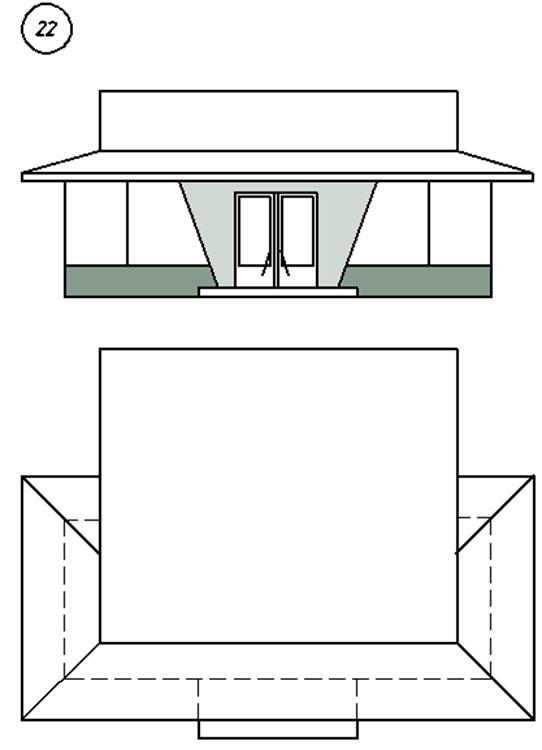
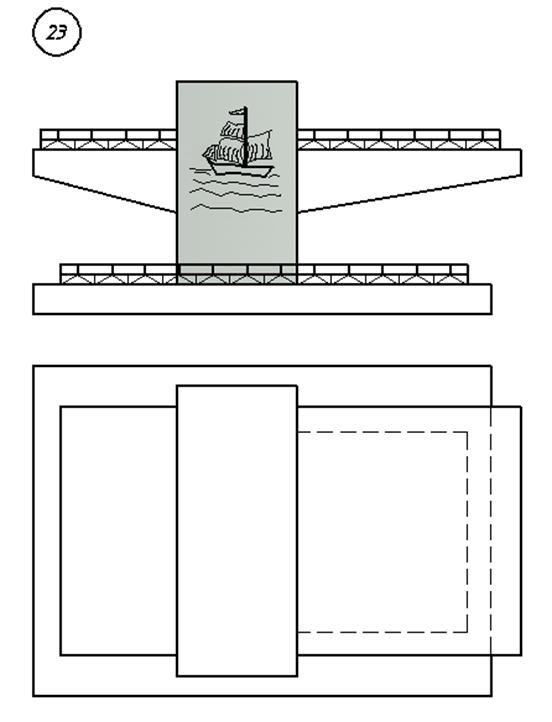
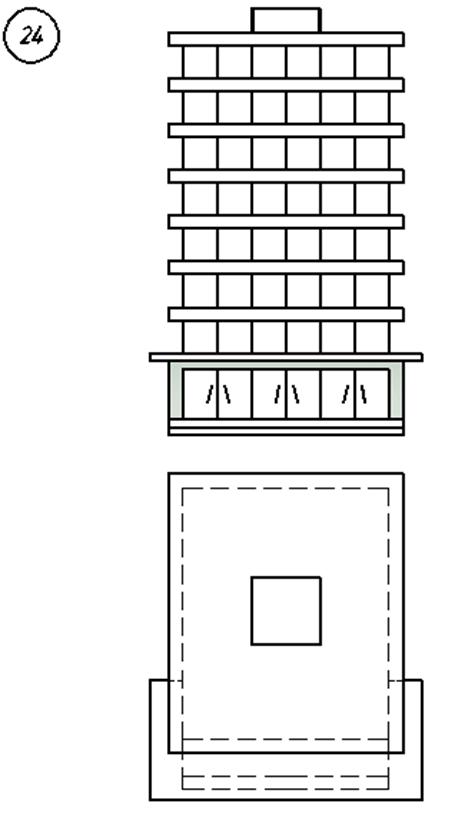
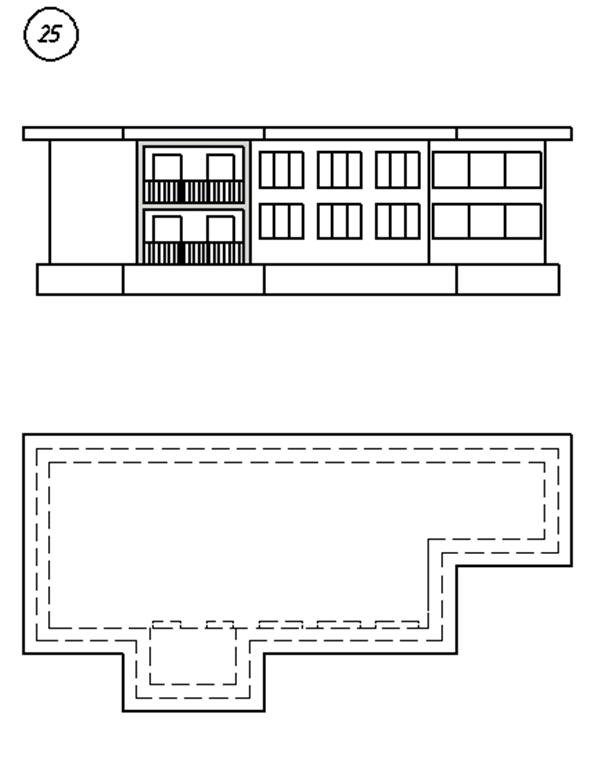
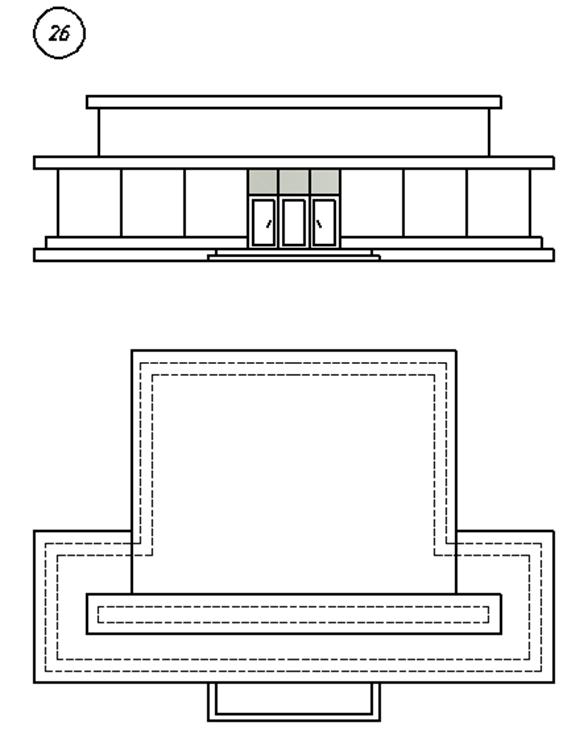
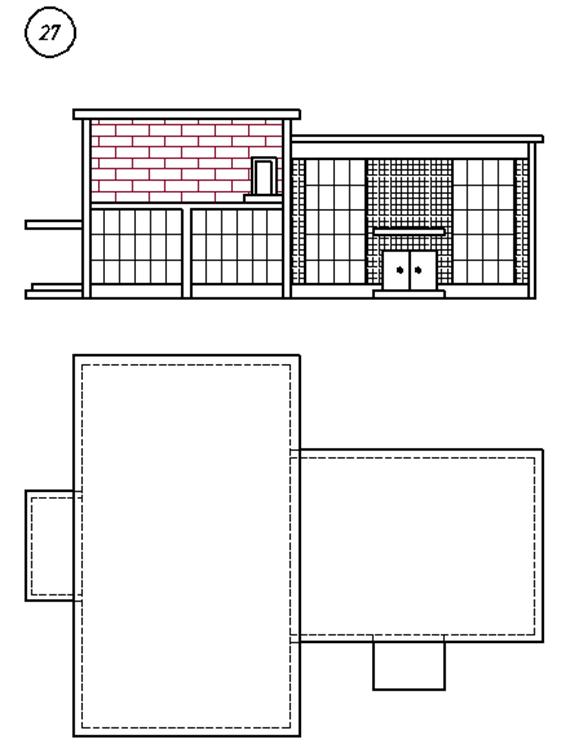
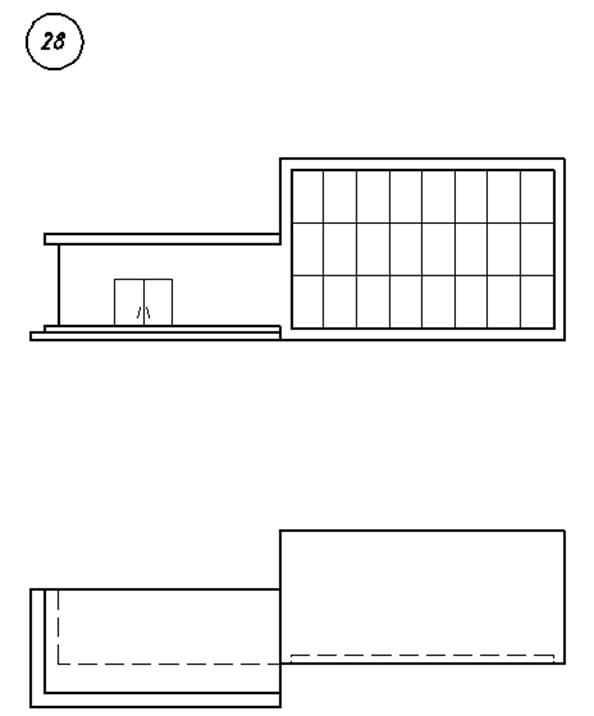
3. Варианты индивидуальных заданий
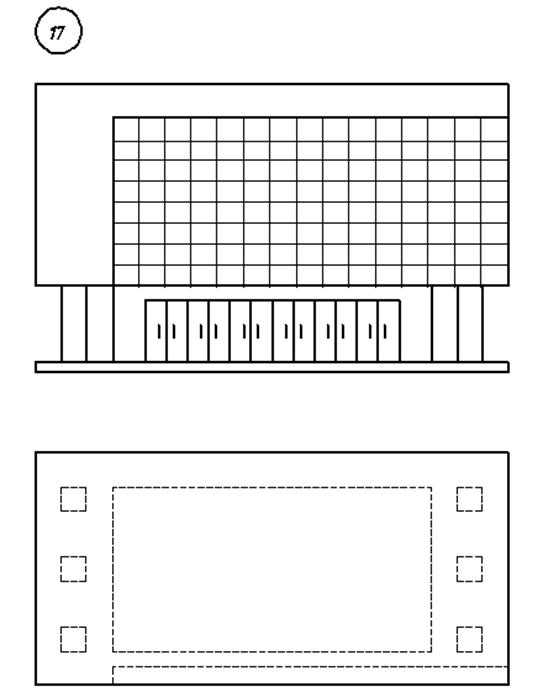
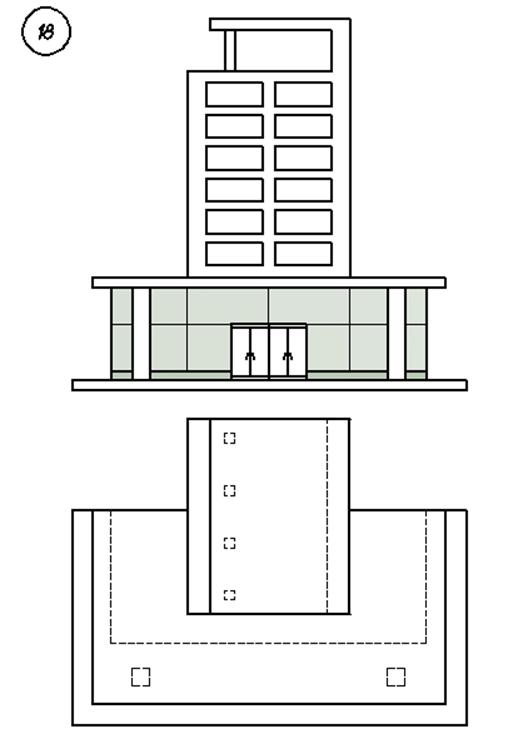
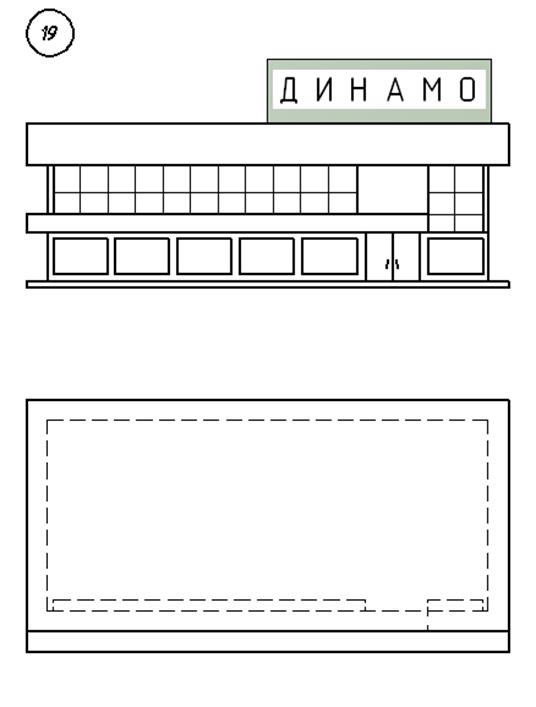
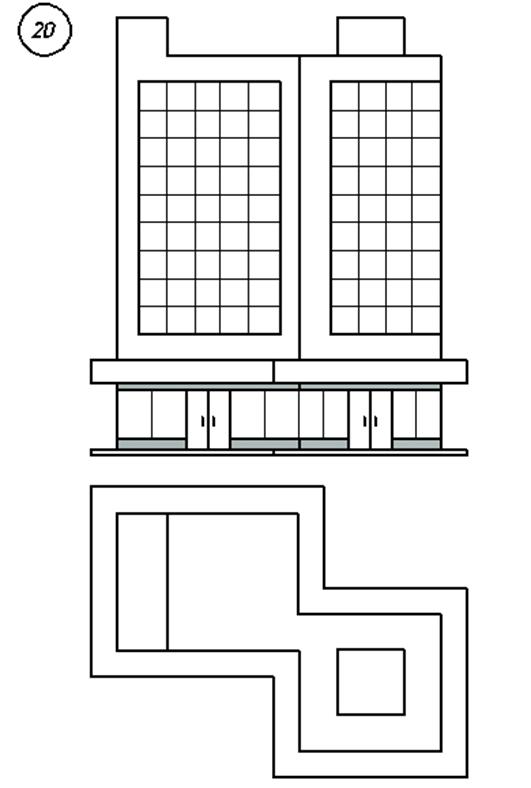
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
‹‹Уральский государственный технический университет — УПИ››
