Перспективный масштаб. Дистанционная точка
Рассмотрим способы построения масштабов измерения длины отрезков, расположенных в трех главных направлениях предметного пространства. Главными направлениями будем считать направление прямых,
1) перпендикулярных картине – направление глубин;
2) параллельных основанию картины – направление широт;
3) перпендикулярных предметной плоскости – направление высот.
Масштаб, построенный на прямой, перпендикулярной картине, называется масштабом глубин.
Введем в системе плоскостей K и T координатные оси X,Y и Z с началом в точке 0, на которых будем строить соответствующие масштабы высот, широт и глубин (рис. 73).
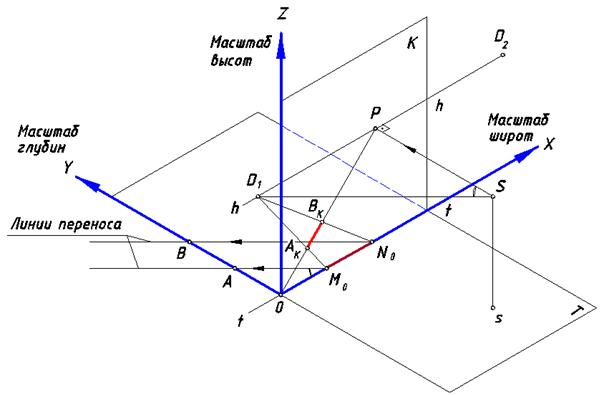
Рис. 73. Построение масштаба глубин
Отложим на оси X случайный отрезок [M0N0]. Если необходимо отложить равный ему отрезок на оси Y поступим следующим образом.
Проведем через точки M0 и N0 вспомогательные прямые в предметной плоскости под углом 45° к оси X. Эти прямые называются линиями переноса. Отметим на оси Y точки A и B. Поскольку ось Y перпендикулярна картине, ее точка схода находится в точке P, а начальная точка находится
в начале координат. Перспектива оси Y на картине отобразилась отрезком [0P].
Начальными точками линий переноса являются точки M0 и N0. Построим перспективу их общей несобственной точки. Для этого через точку S проведем в нее луч, который пересечет картину в точке D на линии горизонта. Соединив начальные точки с точкой D, получим перспективы линий переноса. На пересечении построенных перспектив определим точки AK
и BK.
Точка D называется дистанционной. Поясним, почему она носит такое название. Из построений, приведенных на рис. 73, следует подобие треугольников A0M0 и SPD1. Кроме того, оба треугольника – прямоугольные и равнобедренные, поэтому [SP] = [PD1]. Отрезок [SP] это дистанция между наблюдателем и картиной, и отрезком [PD1] она зафиксирована на линии горизонта на картине. На рисунке выше обозначены две дистанционные точки D1 и D2, которыми можно пользоваться при построении перспективных изображений.
Если требуется отложить равные отрезки на глубинной прямой (прямой, перпендикулярной K), следует поступать так, как показано на
рис. 74.
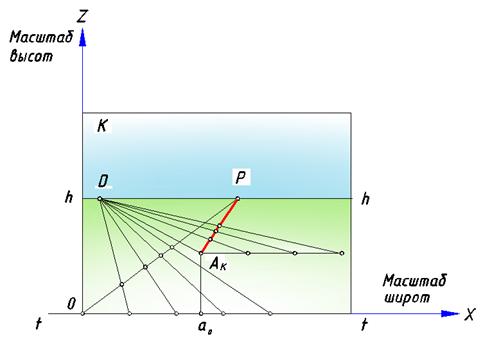
Рис. 74. Построение масштаба на глубинной прямой
Масштаб, построенный на прямой, параллельной основанию картины, называется масштабом широт. Построение масштаба широт показано на рис. 75. Для примера изображены перспективы прямых, находящихся на и вне предметной плоскости.
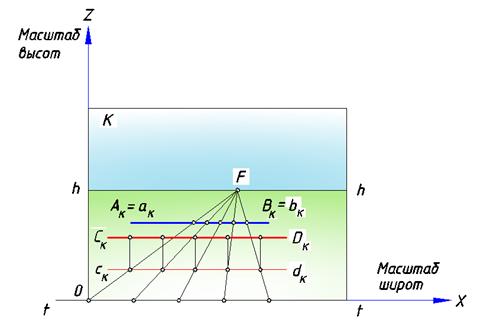
Рис. 75. Построение масштаба на прямой широт
Масштаб, построенный на прямой, перпендикулярной предметной плоскости, называется масштабом высот (рис.76).
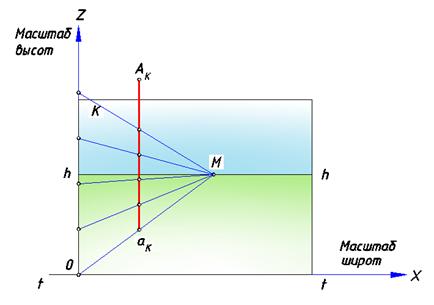
Рис. 76. Построение масштаба на прямой высот
Рассмотрим построение перспективного масштаба на прямой общего положения.
Пусть на предметной плоскости расположена прямая общего положения (рис. 77). Определим начальную точку прямой А0 и ее точку схода F. На картине отрезок [А0F] является перспективой этой прямой. От точки А0 отложим натуральный масштаб (равные отрезки). Через построенные точки в предметной плоскости проведем линии переноса, отсекающие на данной прямой отрезки, равные построенным на линии t – t. Это начальные точки линий переноса. Точка схода этих линий – точка M. Соединив точки 10, 20 и 30 с точкой M, получим перспективные изображения линий переноса. Пересечение построенных линий с отрезком [А0F] зафиксирует отрезки перспективного масштаба на прямой общего положения. Заметим, что на рисунке ниже треугольники A0101' и SFM подобны и равнобедренны по построению, поэтому отрезки [SF] и [FM] равны. Совместим треугольник SFM с плоскостью картины, вращая его вокруг линии горизонта. Тогда отрезок [S1P] на картине будет равен отрезку [SP].
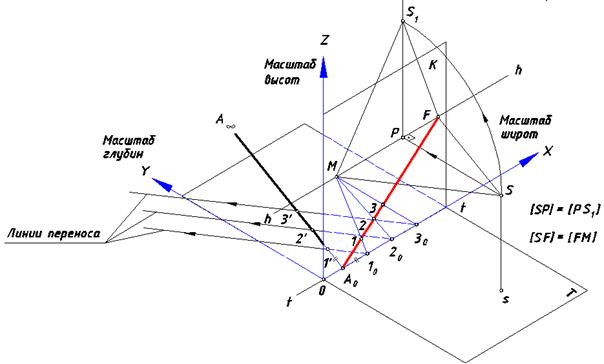
Рис. 77. Построение масштаба на прямой общего положения
При построении перспективы объекта может возникнуть необходимость построения перспективного масштаба на прямой общего положения от какой-либо конкретной точки, например, точки 0 (рис.78).
Пусть на картине дана прямая общего положения (изображенная отрезком [А0F]), дистанционная точка D, главная точка P и точка 0 – начальная точка перспективного масштаба.
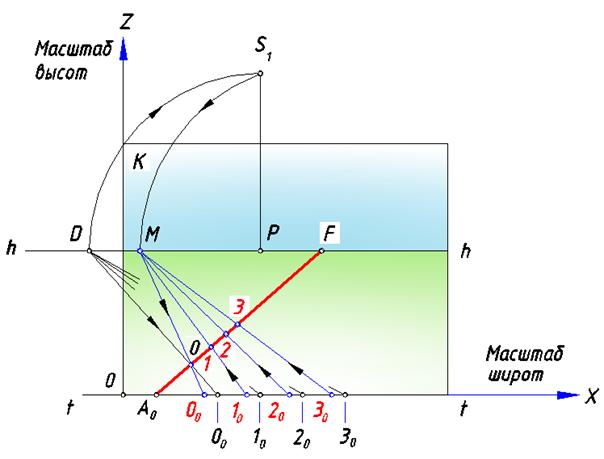
Рис. 78. Картина масштаба на прямой общего положения
В соответствии с рассуждениями, приведенными ранее, на рис. 78. определим точку S1 и точку M. С помощью точки D найдем точку 00, от которой отложим масштабные отрезки на линии t – t (нижние точки на картине). Проведя линию переноса через точки М и 0, найдем начальную точку этой линии 00 (верхняя точкана линии t – t). От нее отложим отрезки, равные нижним. Соединив начальные точки линий переноса с точкой М, на данной прямой общего положения получим перспективный масштаб.
На рис. 79. построена перспективная сетка, с помощью которой можно определять координаты точек какого-либо объекта и его размеры.
Рассмотрим некоторые метрические и позиционные задачи, связанные с использованием перспективных масштабов.
З а д а ч а 1
По заданному перспективному изображению определить координаты точки А (рис. 79).
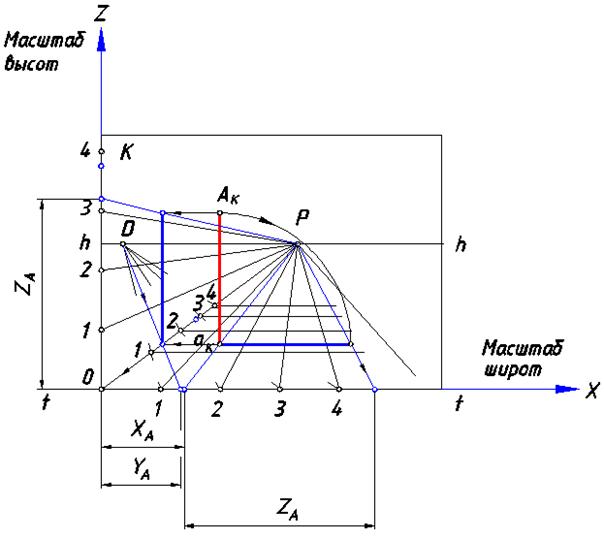
Рис. 79. Перспективная сетка
Опустив из точки aK в предметной плоскости перпендикуляр на ось X (линия построения пройдет через точку P), определим абсциссу XA. Проведем на картине перпендикуляр к оси Y (отрезок [0P]) и отметим точку пересечения с ней. С помощью дистанционной точки D и линии переноса определим натуральную величину ординаты Y. Аппликата ZA найдена двумя способами. В одном случае перспектива аппликаты сдвинута в указанном направлении в картинную плоскость. В другом – использовано свойство равенства перспективных масштабов высот и широт в любой плоскости, параллельной картине.
З а д а ч а 2
Определить натуральные величины данных отрезков по их перспективным изображениям, если на линии горизонта задана точка P
(рис. 80).
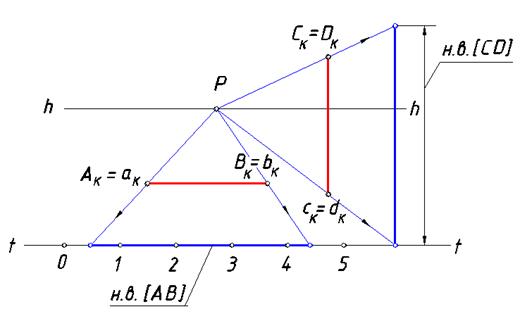
Рис. 80. Определение натуральных величин отрезков прямых,
параллельных картине
З а д а ч а 3
Определить натуральную величину отрезка прямой общего положения. На линии горизонта заданы точки P и D (рис. 81).
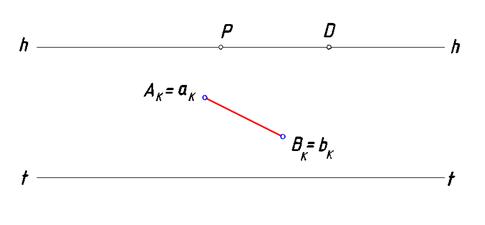
Рис. 81. Условие к задаче 3
По заданной дистанционной точке D определим вспомогательную точку S1. Найдем точку схода F прямой, определяемой точками А и В. Отметим точку схода М линий переноса, с помощью которых можно заданный отрезок общего положения спроецировать на основание картины
и получить его натуральную величину (рис. 82).
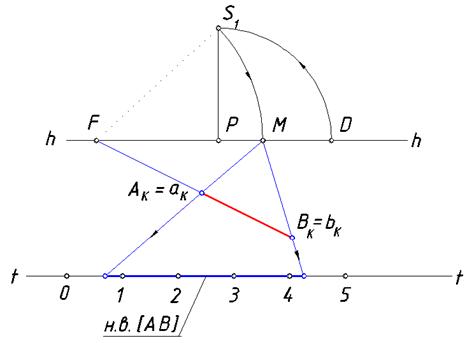
Рис. 82. Решение задачи 3
З а д а ч а 4
Разделить отрезок нисходящей прямой на три части (рис.83).
Используем для решения поставленной задачи теорему Фалеса. Проведем через точку aK (или bK) линию широт, на которой отложим три любых, но равных между собой отрезка. Соединим последнюю точку 3
с точкой bK. Определим точку схода F прямой, содержащей эти точки. Построим прямые, ей параллельные, проходящие через точки 1 и 2. Отметим точки деления на перспективе вторичной проекции данного отрезка. С помощью вертикальных прямых, на основании той же теоремы, найдем искомые точки деления.
Заметим, что при построении перспективы различных архитектурных элементов, расположенных на одинаково небольших расстояниях (таких как ограда, решетка, перила и т. д.) часто применяются геометрические приемы, основанные на теореме Фалеса.
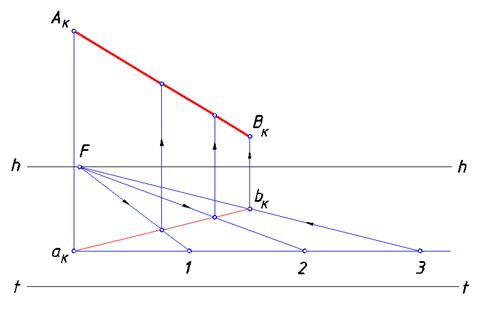
Рис. 83. Деление отрезка на равные части
З а д а ч а 5
Увеличить отрезок восходящей прямой в три раза (рис. 84 и 85).
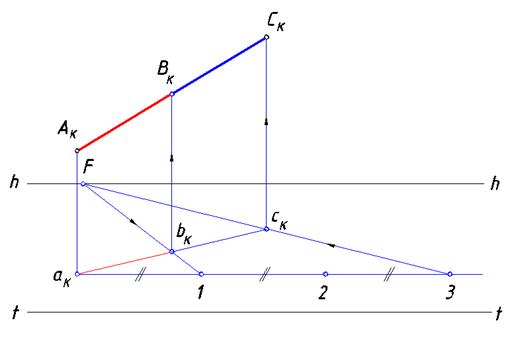
Рис. 84. Первый вариант решения задачи 5
Построим прямую широт, проходящую через точку aK.
На линии горизонтавыберем произвольную точку F линий переноса, с помощью которой перебросим перспективу вторичной проекции отрезка на линию широт. Отметим на ней точку 1. и отложим от нее два отрезка, равных [aK1]. Через точку 3 проведем линию переноса и на продолжении отрезка [aK bK] определим точку cK. Перспектива вторичной проекции отрезка увеличилась в три раза. Проведя через точку cK вертикальную прямую до пересечения с перспективой отрезка, найдем точку СK. Все построения выполнены в соответствии с теоремой Фалеса.
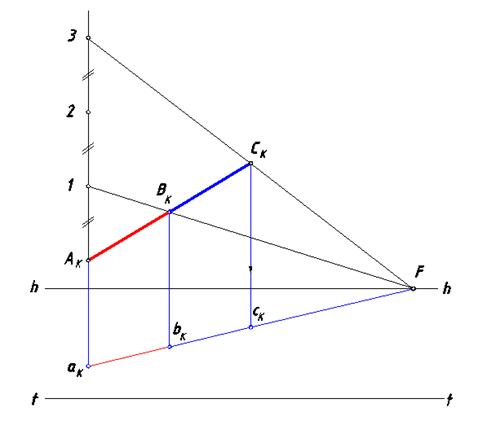
Рис. 85. Второй вариант решения задачи 5
На рис. 85 представлен другой вариант решения этой задачи. Поскольку точка схода F прямой, содержащей точки aK и bK, находится в пределах картины ее можно использовать для увеличения данного отрезка. Проведем через точку АK вертикальную прямую, а через BK – горизонтальную с точкой схода F. Отметим точку 1 пересечения этих прямых. Отложим на вертикальной прямой от точки 1 два единичных отрезка [АK1]. Через точку 3 проведем горизонтальную прямую в точку схода F. Точка пересечения построенной прямой с продолженным отрезком [АK BK] определила конец СKувеличенного в три раза отрезка. Решение задачи вторым способом также основано на применении теоремы Фалеса.
Перспектива плоской фигуры,
