Аппарат линейной перспективы

Перспектива – изображение, построенное на основе центрального проецирования. Такие изображения более наглядны по сравнению с аксонометрическими. Объясняется это тем, что аппарат центрального проецирования наиболее близок к аппарату зрительного восприятия.

Способы изображения формы предметов независимо от их физических качеств изучаются в разделе начертательной геометрии, называемом геометрической перспективой.

Геометрическая перспектива делится

1. на линейную (изображение строится на вертикальной плоскости);

2. панорамную (на цилиндрической поверхности);

3. купольную (на внутренней поверхности сферы);

4. плафонную (на горизонтальной плоскости).

В предлагаемой работе будет рассматриваться только линейная перспектива.

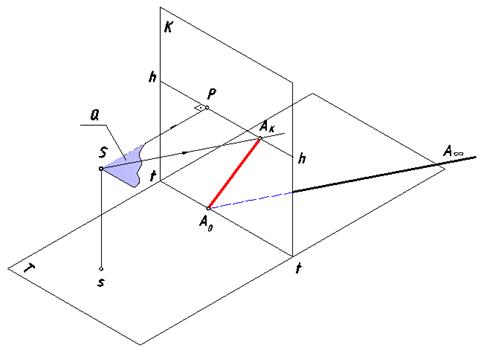
Рис. 62. Аппарат для построения перспективы

К основным элементам перспективного аппарата относятся
(рис. 62):

К – картинная плоскость (или картина);

T – предметная плоскость(земля);

t – t – основание картины;

S – точка зрения (илицентр проекций,или«глаз»);

s – точка стояния;

h – h –линия горизонта;

[SP) –главный луч картины;

P – главная точка картины.

Пусть на предметной плоскости находится прямая линия. Если через точку зрения S провести в каждую точку прямой проецирующий луч, то их множество образует плоскость, которая пересечет картину K по прямой линии. Следовательно, перспективным изображением прямой будетпрямая линия.

Дополним Евклидово пространство несобственными элементами: несобственная или бесконечно удаленная точка, несобственная прямая
и несобственная плоскость. Такое пространство называется проективным.

Если в Евклидовом пространстве параллельные прямые не пересекались, то в проективном – параллельные прямые образуют пучок с общей несобственной точкой (центром пучка).

Представим, что на предметной плоскости расположено множество прямых линий различного направления по отношению к картине. У каждой такой прямой есть своя несобственная точка. Множество таких точек образует бесконечно удаленную прямую плоскости T.

Лучи зрения, проходящие через точку S и каждую несобственную точку прямой, образуют плоскость, параллельную предметной. Такая плоскость называется плоскостью горизонта и пересекает картину по прямой h – h – линии горизонта. Поэтому эту линию можно считать перспективой несобственной прямой.

Построим перспективу данной прямой. Известно, что любая прямая определяется парой несовпадающих точек. Одну из таких точек можно определить, если продолжить данную прямую до пересечения с картиной (точку A₀). Назовем эту точку «начальной точкой прямой».

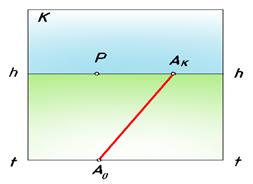
Рис. 63. Перспектива прямой, лежащей в предметной плоскости

Затем определим перспективу бесконечно удаленной точки A_∞,проведя через точку S и эту точку луч, параллельный предметной плоскости. Пересечение луча с картиной определит точку A_К. Назовем ее предельной или точкой схода прямой, или «конечной точкой» прямой. Соединив точку A_К с точкой A₀ получим перспективу данной прямой, изображенную конечным отрезком [A₀ A_К] на рис. 63.

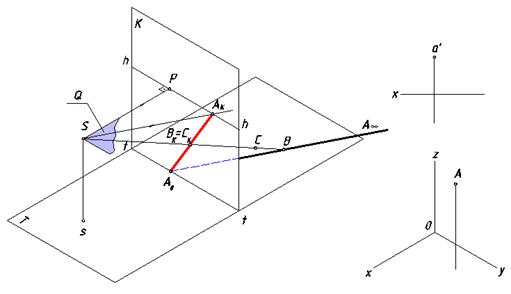
Рис. 64. Неопределенные чертежи

Если на этой прямой взять случайную точку B и провести через нее луч, то перспектива точки (точка B_К) определится пересечением луча
с картиной и будет принадлежать отрезку [A₀ A_К]. Но с этой же точкой совпадают перспективы всех точек проведенного луча (например, точки С)
и т.о. приведенный чертеж становится неопределенным. На рис. 64 приведены примеры чертежей такого рода и в параллельных проекциях.

Поэтому и в центральных проекциях, также как и в параллельных для однозначного прочтения любого геометрического объекта требуется наличие двух его проекций, которые полностью определят его положение в пространстве и позволят решать как метрические, так и позиционные задачи.

Поступим следующим образом: возьмем за картинной плоскостью точку А (оригинал) с ее вторичной проекцией на предметной плоскости – точкой а (рис. 65). Из точки зрения проведем луч в эту точку. Луч и отрезок [Ss] задают плоскость, перпендикулярную Т, на основании признака перпендикулярности двух плоскостей. Построим линию пересечения проведенной плоскости и плоскости К. Поскольку обе плоскости перпендикулярны Т, их линия пересечения будет вертикальной прямой.

Отметим на ней точку а₀. Пересечение проведенного луча с этой прямой определит перспективу точки А – точку A_К. Построим перспективу вторичной проекции а, проведя луч из точки S в эту точку. Точка пересечения луча с картинной плоскостью а_К – перспектива вторичной проекции точки (точки на земле).

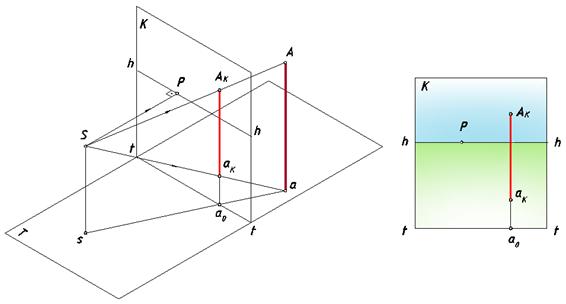
Рис. 65. Вертикальная прямая (столб) в перспективе

Перспектива прямых линий

Заметим, что в линейной перспективе принято допущение: прямые, параллельные картине, точек схода не имеют.

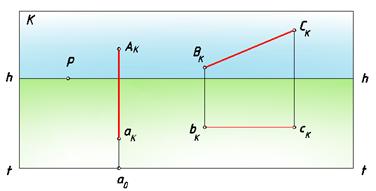
Рис. 66. Перспективы прямых, параллельных картине

Рисунок, приведенный выше, иллюстрирует это положение.

Рассмотрим перспективу пучка параллельных прямых произвольного направления, параллельных предметной плоскости.

Пучок – это множество прямых, проходящих через данную точку.
В проективном пространстве эта точка может быть несобственной (бесконечно удаленной).

На рис. 67 изображены параллельные прямые произвольного направления, две из которых расположены в предметной плоскости, а третья ей параллельна. Ранее отмечалось, что перспективу прямой линии можно построить по двум точкам: начальной и конечной.

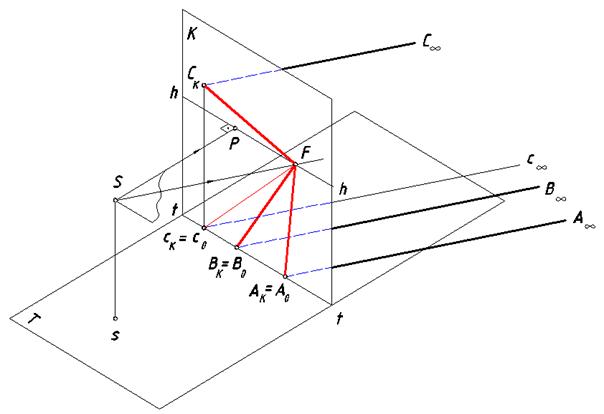
Рис. 67. Пучок параллельных прямых произвольного направления

Начальные точки всех прямых и их вторичных проекций отмечены на рисунке выше (это точки пересечения прямых с картиной). Поскольку все данные прямые параллельны, то в проективном пространстве у них есть общая бесконечно удаленная точка. Для построения ее перспективы через точку S проводим луч в эту точку (на приведенном изометрическом рисунке он параллелен этим прямым) и отмечаем точку его пересечения
с картиной – это перспектива общей несобственной точки данных прямых или точка схода прямых.

Соединив начальные точки данных прямых с точкой схода F, получаем изображение пучка прямых на картине (рис. 68).

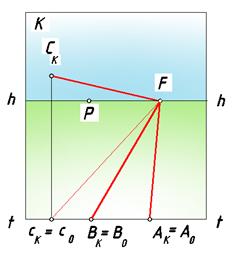
Рис. 68. Картина пучка параллельных прямых

произвольного направления

На рис. 69 представлено наглядное изображение прямых линий, перпендикулярных картине.

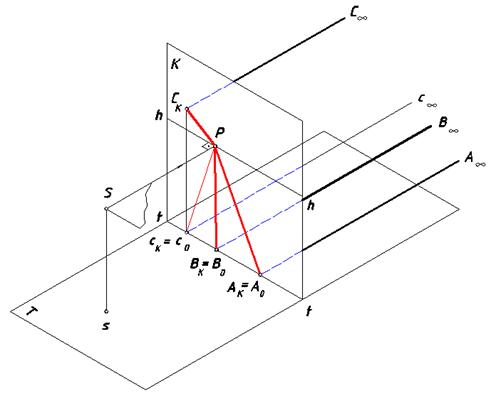
Рис. 69. Пучок прямых, перпендикулярных картине

Как и в предыдущем случае, у этих прямых существует общая несобственная точка. Для нахождения ее перспективы через точку S проводим луч, параллельный этим прямым, в эту бесконечно удаленную точку. Пересечение проведенного луча с картиной происходит в точке P – главной точке картины, которая является точкой схода этих прямых.Соединяем начальные точки прямых с точкой P и получаем перспективное изображение этих прямых (рис. 70).

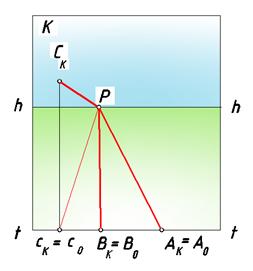
Рис. 70. Перспектива пучка прямых, перпендикулярных картине

Сравним рисунки, представленные ниже. На каждом из них изображена плоская фигура, выделенная темным оттенком. На рис. 71, а она представляет собой прямоугольник, а на рис. 71, б – параллелограмм.

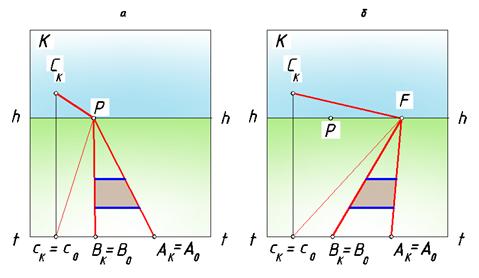
Рис. 71. Рисунки плоских фигур

Введем понятия восходящих и нисходящих прямых линий.

Восходящими называются прямые, которые идут, возвышаясь от картины. Поэтому. каждая следующая за картиной точка, взятая на прямой, имеет большую высоту, чем предыдущая. Нисходящие прямые идут, понижаясь от картины.

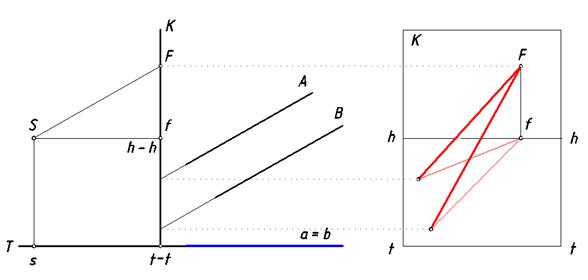
Рис. 72. Восходящие прямые

На рис. 72 слева показаны две параллельные восходящие прямые (картина и предметная плоскость изображены двумя перпендикулярными линиями). Из этого чертежа наглядно следует только то, что данные прямые являются восходящими, но полной информации об этих линиях не дано. Тем не менее, из рисунка следует, что точка схода этих прямых
(точка F) расположена выше линии горизонта. Вторичные проекции этих линий лежат на предметной плоскости. Поскольку предметная плоскость отображена прямой линией – вторичные проекции прямых на рисунке совпадают. Вторичные проекции линий параллельны на основании свойства параллельных проекций, их точка схода f находится на линии горизонта. На рис. 72 справа хорошо видно, что точки F и f находятся в проекционной связи на перпендикуляре к линии h – h. Заметим, что этот рисунок иллюстрирует перспективу случайных восходящих параллельных прямых и не имеет прямой связи с рисунком слева. Изображенные прямые занимают
в пространстве общее положение. Если параллельные восходящие прямые будут параллельны воображаемой плоскости, перпендикулярной одновременно плоскостям T и K, то точкой схода их вторичных проекций будет главная точка картины P, а сами прямые сойдутся на перспективном чертеже в точке F, находящейся выше линии горизонта, в проекционной связи с точкой P.

У пучка нисходящих прямых точка схода находится ниже линии горизонта.