Теорема о взаимности реакций и перемещений
На рис. 15.5 показаны два состояния произвольной статически неопределимой системы (рамы). В первом состоянии (состоянии i) на раму действует обобщённая сила Fi = 1. Опорная связь j получает единичное перемещение во втором состоянии (состоянии j). Введём обозначения: r'ji – реакция в j-й связи от обобщённой силы Fi = 1 в состоянии i, d'ij – перемещение по направлению обобщённой силы Fi = 1 от смещения связи j на единицу в состоянии j. За положительное направление перемещения d'ij примем перемещение, происходящее по направлению обобщённой силы Fi = 1, а за положительную реакцию r'ji реакцию, направление которой совпадает с перемещением j-й связи.

Для состояний i и j используем теорему о взаимности возможных работ внешних сил (см. соотношение (15.3) в п. 15.1).
Wext,ij = 1 × d'ij + r'ji × 1.
Возможная работа Wext,ji внешних сил состояния j на перемещениях, вызываемых внешними силами состояния i, равна нулю, так как в состоянии i перемещения по направлению опорных связей в том числе и по направлению связи j, отсутствуют, т.е.
Wext,ji = 0.
В соответствии с выражением (15.3) Wext,ij = Wext,ji, поэтому
1 × d'ij + r'ji × 1 = 0, или r'ji = –d'ji. (15.6)
Соотношение (15.6) является математической формулировкой теоремы о взаимности реакций и перемещений: реакция в j-й связи сооружения от обобщённой силы Fi = 1 с обратным знаком численно равна перемещению в направлении i-й обобщённой силы от смещения j-й связи на единицу (вторая теорема Рэлея).
При определении размерности величины r'ji и d'ji необходимо учитывать их удельный характер, т.е. то обстоятельство, что они вызываются, соответственно, единичной обобщённой силой и единичным смещением связи.
Теорема о взаимности реакций и перемещений применяется в расчётах статически неопределимых систем смешанным методом.
Вопросы для самопроверки
1. Сформулируйте теорему о взаимности возможных работ внешних сил. Какие теоремы взаимности строительной механики вытекают из этой теоремы?
2.  Сформулируйте теорему о взаимности перемещений и запишите её в математической форме.
Сформулируйте теорему о взаимности перемещений и запишите её в математической форме.
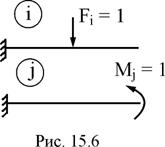
3.  Консольный стержень в состоянии i загружен сосредоточенной силой Fi = 1, а в состоянии j – сосредоточенным моментом Mj = 1 (рис. 15.6). Покажите на чертеже возможные перемещения dij и dji. Какую размерность имеют величины этих перемещений?
Консольный стержень в состоянии i загружен сосредоточенной силой Fi = 1, а в состоянии j – сосредоточенным моментом Mj = 1 (рис. 15.6). Покажите на чертеже возможные перемещения dij и dji. Какую размерность имеют величины этих перемещений?
4. Сформулируйте теорему о взаимности реакций и запишите её в математической форме.
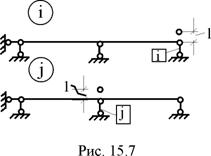
5. В двухпролётной неразрезной балке в состоянии i правая опорная связь получает перемещение вверх на единицу, а в состоянии j перемещение на единицу в таком же направлении получает средняя опорная связь (рис. 15.7). Покажите на чертеже реакции rij и rji. Какую размерность имеют величины этих реакций?
6.  Сформулируйте теорему о взаимности реакций и перемещений и запишите её в математической форме.
Сформулируйте теорему о взаимности реакций и перемещений и запишите её в математической форме.
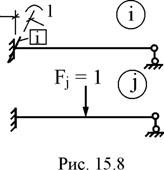
7. В стержне, защемлённом на левом конце и шарнирно опёртом на правом, в состоянии i левая угловая связь i повёрнута на угол равный единице, а в состоянии j на стержень действует единичная сосредоточенная сила Fj = 1 (рис. 15.8). Покажите на чертеже реакцию r'ij и перемещение d'ji. Какую размерность имеют величины r'ij и d'ji?
15.6. Рекомендуемая литература
1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.
Гл. 5. Основы теории расчёта линейно деформируемых систем. § 5.5. Теоремы о взаимности. – С. 104–109.
2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.
Гл. 5. Определение перемещений в упругих системах. § 5.2. Теорема о взаимности работ. § 5.3. Теорема о взаимности перемещений. – С. 163–168.
3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.
Гл. IX. Основные энергетические теоремы. Свойства матриц податливости и жёсткости. § 48. Теоремы о взаимности. – С. 255–262.
Лекция шестнадцатая
