Теоремы взаимности строительной механики
Лекция пятнадцатая
Теоремы взаимности строительной механики
15.1. Теорема о взаимности возможных работ
15.2. Теорема о взаимности перемещений
15.3. Теорема о взаимности реакций
15.4. Теорема о взаимности реакций и перемещений
15.5. Вопросы для самопроверки
15.6. Рекомендуемая литература
Теорема о взаимности перемещений
По-прежнему рассмотрим состояния i и j одного и того же сооружения (рис. 15.2). В состоянии i на него действует сила Fi = 1, а в состоянии j – сила Fj = 1. Зафиксируем возможные перемещения dij и dji, возникающие в состояниях i и j от единичных сил.
Для состояний сооружения i и j применим теорему о взаимности возможных работ внешних сил (см. п. 15.1, соотношение (15.3)):
1 × dij = 1 × dji, или dij = dji. (15.4)
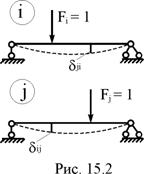 Соотношение (15.4) выражает содержание теоремы о взаимности перемещений: перемещение по направлению линии действия i-й единичной обобщённой силы, вызванное j-й единичной обобщённой силой, равно перемещению по направлению линии действия j-й обобщённой силы от i-й единичной обобщённой силы. В строительной механике эта теорема известна как теорема английского физика и механика Джеймса Максвелла (1831–1879).
Соотношение (15.4) выражает содержание теоремы о взаимности перемещений: перемещение по направлению линии действия i-й единичной обобщённой силы, вызванное j-й единичной обобщённой силой, равно перемещению по направлению линии действия j-й обобщённой силы от i-й единичной обобщённой силы. В строительной механике эта теорема известна как теорема английского физика и механика Джеймса Максвелла (1831–1879).
Теорема о взаимности перемещений широко применяется в расчётах линейно деформируемых систем, в частности, в расчётах статически неопределимых систем методом сил, при построении линий влияния перемещений в стержневых сооружениях.
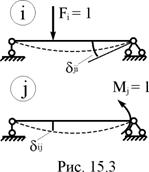 Выше был рассмотрен случай, когда в состоянии i и j сооружения действуют единичные сосредоточенные силы (рис. 15.2), т.е. силы, имеющие одинаковую природу и одинаковую размерность. На рис. 15.3 рассмотрена ситуация, когда в состоянии i на сооружение действует сосредоточенная сила Fi = 1, а состоянии j – сосредоточенный момент Mj = 1. Здесь же показаны и возможные перемещения dij и dji, вызываемые упомянутыми силами Fi = 1 и Mj = 1. Кажущееся противоречие в размерностях перемещений dij и dji, равенство которых определено соотношением (15.4), отпадает, если мы примем во внимание, что каждое из этих перемещений является удельным перемещением, т.е. что оно вызывается обобщённой силой, имеющей не произвольное, а единичное значение. Таким образом, размерность какого-либо удельного перемещения есть отношение размерности рассматриваемого обобщённого перемещения к размерности обобщённой силы, вызвавшей это перемещение. В случае, рассмотренном на рис. 15.3, имеем:
Выше был рассмотрен случай, когда в состоянии i и j сооружения действуют единичные сосредоточенные силы (рис. 15.2), т.е. силы, имеющие одинаковую природу и одинаковую размерность. На рис. 15.3 рассмотрена ситуация, когда в состоянии i на сооружение действует сосредоточенная сила Fi = 1, а состоянии j – сосредоточенный момент Mj = 1. Здесь же показаны и возможные перемещения dij и dji, вызываемые упомянутыми силами Fi = 1 и Mj = 1. Кажущееся противоречие в размерностях перемещений dij и dji, равенство которых определено соотношением (15.4), отпадает, если мы примем во внимание, что каждое из этих перемещений является удельным перемещением, т.е. что оно вызывается обобщённой силой, имеющей не произвольное, а единичное значение. Таким образом, размерность какого-либо удельного перемещения есть отношение размерности рассматриваемого обобщённого перемещения к размерности обобщённой силы, вызвавшей это перемещение. В случае, рассмотренном на рис. 15.3, имеем:
[dij] = 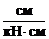 = кН-1, [dji] =
= кН-1, [dji] = 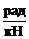 = кН-1,
= кН-1,
т.е. оба перемещения имеют одинаковую размерность.
Вопросы для самопроверки
1. Сформулируйте теорему о взаимности возможных работ внешних сил. Какие теоремы взаимности строительной механики вытекают из этой теоремы?
2.  Сформулируйте теорему о взаимности перемещений и запишите её в математической форме.
Сформулируйте теорему о взаимности перемещений и запишите её в математической форме.
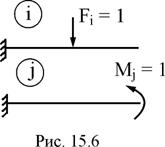
3.  Консольный стержень в состоянии i загружен сосредоточенной силой Fi = 1, а в состоянии j – сосредоточенным моментом Mj = 1 (рис. 15.6). Покажите на чертеже возможные перемещения dij и dji. Какую размерность имеют величины этих перемещений?
Консольный стержень в состоянии i загружен сосредоточенной силой Fi = 1, а в состоянии j – сосредоточенным моментом Mj = 1 (рис. 15.6). Покажите на чертеже возможные перемещения dij и dji. Какую размерность имеют величины этих перемещений?
4. Сформулируйте теорему о взаимности реакций и запишите её в математической форме.
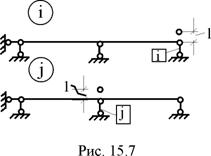
5. В двухпролётной неразрезной балке в состоянии i правая опорная связь получает перемещение вверх на единицу, а в состоянии j перемещение на единицу в таком же направлении получает средняя опорная связь (рис. 15.7). Покажите на чертеже реакции rij и rji. Какую размерность имеют величины этих реакций?
6.  Сформулируйте теорему о взаимности реакций и перемещений и запишите её в математической форме.
Сформулируйте теорему о взаимности реакций и перемещений и запишите её в математической форме.
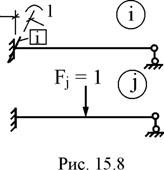
7. В стержне, защемлённом на левом конце и шарнирно опёртом на правом, в состоянии i левая угловая связь i повёрнута на угол равный единице, а в состоянии j на стержень действует единичная сосредоточенная сила Fj = 1 (рис. 15.8). Покажите на чертеже реакцию r'ij и перемещение d'ji. Какую размерность имеют величины r'ij и d'ji?
15.6. Рекомендуемая литература
1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.
Гл. 5. Основы теории расчёта линейно деформируемых систем. § 5.5. Теоремы о взаимности. – С. 104–109.
2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.
Гл. 5. Определение перемещений в упругих системах. § 5.2. Теорема о взаимности работ. § 5.3. Теорема о взаимности перемещений. – С. 163–168.
3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.
Гл. IX. Основные энергетические теоремы. Свойства матриц податливости и жёсткости. § 48. Теоремы о взаимности. – С. 255–262.
Лекция шестнадцатая
Пример расчёта статически неопределимой рамы методом сил
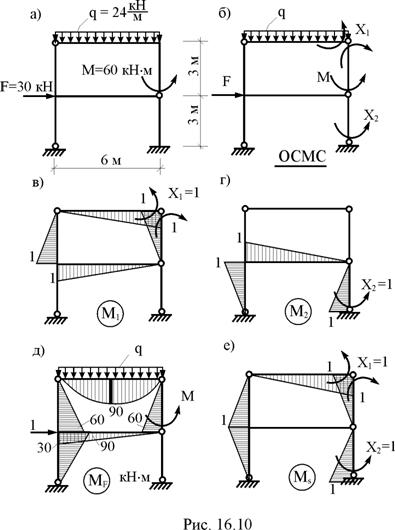
Построить эпюры внутренних усилий от силового воздействия в раме, изображённой на рис. 16.10,а, если известно, что изгибная жёсткость поперечных сечений ригелей рамы EJp вдвое больше изгибной жёсткости поперечных сечений её стоек EJс, т.е. EJp : EJс = 2 : 1.
1. Определение степени статической неопределимости рамы по формуле "контуров" (14.1).
nst = 3K – H = 3 × 2 – 4 = 2.
При вычислении nst учтено, что шарнир правой стойки рамы, соединяющий в узле три диска, эквивалентен двум простым шарнирам.
2. Выбор основной системы метода сил и её кинематический анализ. Основную систему образуем введением цилиндрических шарниров в верхний и нижний узлы правой стойки рамы, т.е. удалением связей, препятствующих взаимному повороту двух соседних сечений верхнего правого узла рамы и повороту сечения, расположенному близко к правому опорному защемлению рамы. За неизвестные метода сил в нашем случае принимаются усилия в удалённых угловых связях, а именно – изгибающие моменты Х1 и Х2 (рис. 16.10,б).
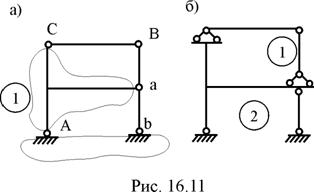
Принятая для расчёта основная система метода сил с кинематической точки зрения имеет простую структуру и геометрически неизменима. Действительно, диск 1 основной системы закрепляется к диску "земля" цилиндрическим шарниром А и связью ab, ось которой не проходит через шарнир А (рис. 16.11,а). К геометрически неизменяемой структуре AbaС узел В присоединён диадой (двумя связями СВ и аВ).
3. Построение эпюр изгибающих моментов в основной системе метода сил от Х1 = 1 (рис. 16.10,в), Х2 = 1 (рис. 16.10,г) и заданной нагрузки (рис. 16.10,д). Эти эпюры читателям предлагается построить самостоятельно, приняв во внимание рабочую схему основной системы (рис. 16.11,б), на которой показаны её главная и второстепенная части и определён порядок расчёта.
4. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений:
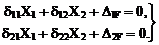
Сопряжение соответствующих эпюр изгибающих моментов будем производить, используя формулу Симпсона и правило Верещагина (см. п. 11.4 второй части настоящего курса лекций). Напоминаем, что определение коэффициентов dii, dij и DiF в рамных и балочных системах производится только с учётом изгибных деформаций по формулам (16.8)–(16.10).
Примем EJp = 2EJ, EJс = EJ (EJ – произвольное число), сохраняя заданное соотношение между изгибными жесткостями поперечных сечений ригелей и стоек рамы.
Читателям рекомендуется тщательно проверить арифметические выражения, записанные ниже для численных значений определённых интегралов формулы Мора.
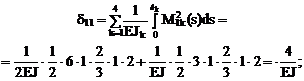
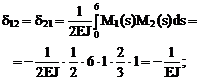
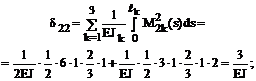
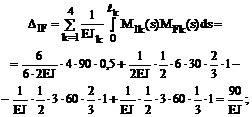
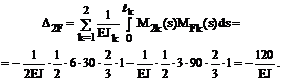
5. Проверка правильности вычисления коэффициентов при неизвестных и грузовых коэффициентов системы канонических уравнений. Суммарная эпюра изгибающих моментов Ms = M1+M2 от Х1 = 1 и Х2 = 1 в основной системе метода сил показана на рис. 16.10,е.
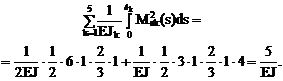
Результат сопряжения эпюры изгибающих моментов Ms саму на себя равен сумме
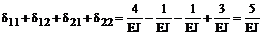 ,
,
что подтверждает достоверность вычисления коэффициентов при неизвестных.
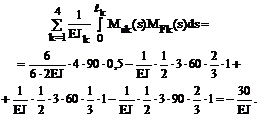
Сумма ранее вычисленных грузовых коэффициентов системы канонических уравнений
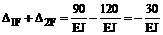
совпадает с результатами сопряжения эпюр изгибающих моментов Ms и MF, что свидетельствует о правильности их вычисления.
6. Решение системы канонических уравнений:
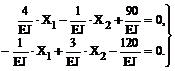
В заданной системе уравнений абсолютное значение жёсткости поперечного сечения стоек рамы EJc = EJ сокращается, т.е. величины усилий в лишних связях Х1 и Х2 и, следовательно, значения внутренних усилий от заданной нагрузки во всех сечениях рамы зависят от относительного значения изгибных жесткостей поперечных сечений элементов рамы. Этот вывод распространяется на любые статически неопределимые стержневые системы при их расчёте на силовое воздействие.
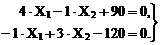
Отсюда получим: Х1 = -13,64 кН×м, Х2 = 35,45 кН×м. Знак "минус" для числового значения усилия в лишний связи Х1 указывает на обратное направление действия этого усилия по сравнению с предварительно принятым при выборе основной системе метода сил.
7. Определение изгибающих моментов в сечениях заданной рамы и построение соответствующей эпюры. Для рассматриваемой задачи соотношение (16.11) примет вид:
M = M1X1 + M2X2 + MF.
Ординаты эпюры М1 умножим на –13,64 кН×м, а М2 – на 35,45 кН×м, затем произведём сложение эпюр М1Х1, М2Х2 и MF (рис. 16.12). Эпюра изгибающих моментов заданной раме показана рис. 16.13,а.
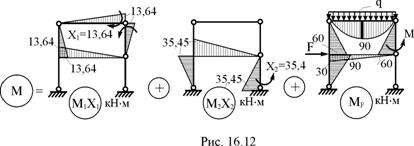
8. Кинематическая проверка. Для этой цели используем суммарную эпюру изгибающих моментов Ms (рис. 16.10,е)
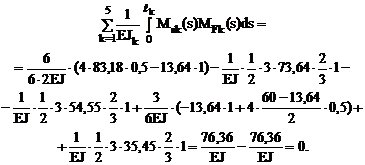
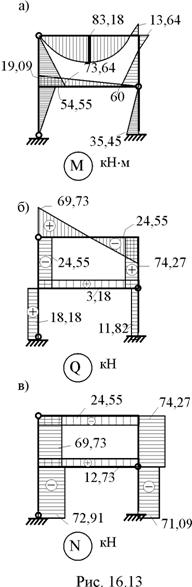 Кинематическая проверка выполнена с нулевой абсолютной погрешностью.
Кинематическая проверка выполнена с нулевой абсолютной погрешностью.
9. Построение эпюр поперечных и продольных сил в заданной раме. Читателям предлагается, используя методику, изложенную в п. 5.4 первой части настоящего курса лекций, эпюру поперечных сил построить по эпюре изгибающих моментов, а эпюру продольных сил – по эпюре поперечных сил. Эпюры Q и N для заданной рамы показаны на рис. 16.13,б,в.
Пример расчёта статически неопределимой рамы методом сил в матричной форме
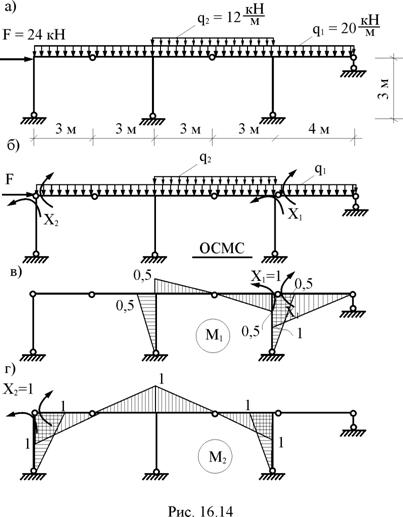
В раме, показанной на рис. 16.14,а, построить эпюры внутренних усилий отдельно от постоянной равномерно распределённой нагрузки q1 = 20 кН/м, первой временной равномерно распределённой нагрузки q2 = 12 кН/м, второй временной нагрузки – сосредоточенной силы F = 24 кН, а также вычислить расчётные изгибающие моменты в её характерных сечениях. Соотношение между изгибными жесткостями поперечных сечений ригеля и стоек задано: EJp : EJc = 2 : 0,5.
Порядок расчёта рамы на заданные воздействия в матричной форме определяется соотношением (16.28):
M(F) = MF – M(MT BM M)-1(MT BM MF).
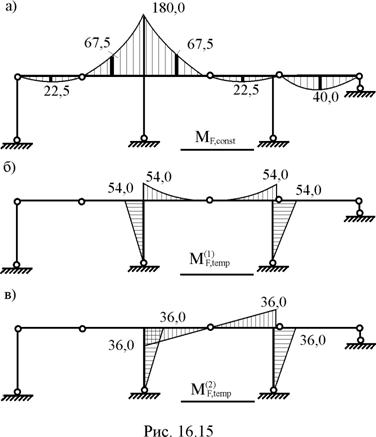
1. Подготовительный этап расчёта: определение степени статической неопределимости рамы (nst = 3 × 3 – 7 = 2), выбор основной системы метода сил (рис. 16.14,б), построение эпюр изгибающих моментов в основной системе от Х1 = 1, Х2 = 1 (рис. 16.14,в,г), постоянной нагрузки (рис. 16.15,а), первой временной (рис. 16.15,б) и второй временной нагрузки (рис. 16.15,в).
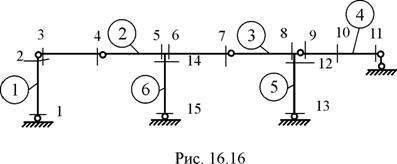
2. Нумерация грузовых участков и сечений, необходимых для формирования матриц изгибающих моментов M и MF (рис. 16.16).
3. Формирование матриц изгибающих моментов M и MF от Х1 = 1, Х2 = 1 и заданных нагрузок (постоянной и временных) в основной системе метода сил в соответствии с принятой нумерацией грузовых участков и сечений. Правило знаков для элементов этих матриц было сформулировано ранее (см. пример 13.4.1 тринадцатой лекции).

4. Формирование матрицы внутренней упругой податливости рамы, учитывающей изгибные деформации её грузовых участков. Примем EJp = 2EJ, EJс = 0,5EJ (EJ – произвольное число).


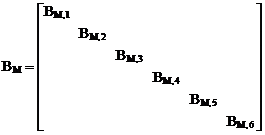 ,
,
где 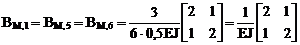 ;
;
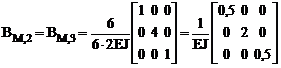 ;
; 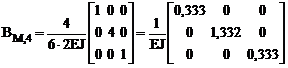 .
.
5. Вычисление элементов матрицы внешней податливости принятой для расчёта основной системы метода сил, или матрицы коэффициентов при неизвестных d системы канонических уравнений.
d = МT BМ М = 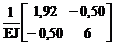 .
.
6. Вычисление элементов матрицы грузовых коэффициентов, или матрицы свободных членов DF системы канонических уравнений
DF = МT BМ МF = 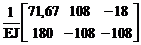 .
.
7. Обращение матрицы внешней податливости d.
d × d-1 = Е, 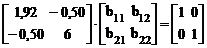 .
.
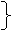 1,92b11 – 0,5b21 = 1,
1,92b11 – 0,5b21 = 1,
-0,5b12 + 6b21 = 0.
Отсюда b11 = 0,533, b21 = 0,044.
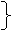 1,92b12 – 0,5b22 = 0,
1,92b12 – 0,5b22 = 0,
-0,5b12 + 6b22 = 1.
Отсюда b12 = 0,044, b22 = 0,170.
d-1 = (МT BМ М)-1 = 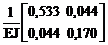 .
.
8. Вычисление элементов матрицы неизвестных метода сил Х.
X = –d-1 DF = –(МT BМ М)-1(МT BМ МF) =
= 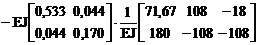 =
=
= 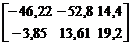 .
.
9. Вычисление элементов матрицы изгибающих моментов M(F) в заданной раме от постоянной и временной нагрузок.
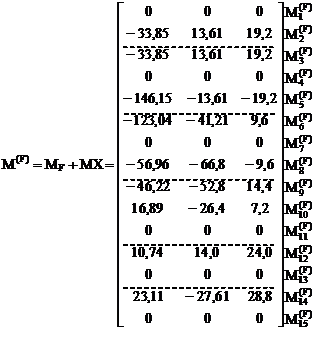
10. Кинематическая проверка правильности вычисления элементов матрицы M(F), являющихся ординатами эпюр изгибающих моментов в заданной раме от постоянной, первой и второй временных нагрузок в сечениях, показанных на рис. 16.16.
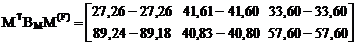 .
.
Относительные погрешности вычислений при сопряжении окончательных эпюр изгибающих моментов, описываемых элементами матрицы M(F), с соответствующими эпюрами от Х1 = 1 и Х2 = 1 в основной системе метода сил, описываемых элементами матрицы М, не превышают 0,07 %.
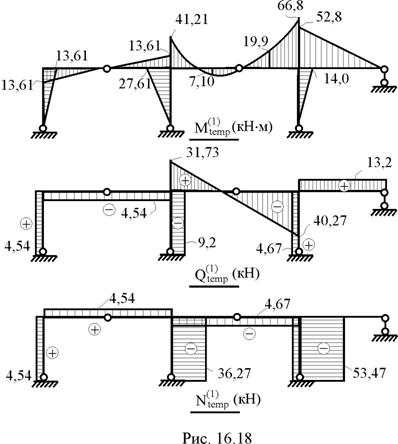
11. Построение эпюр изгибающих моментов в заданной раме Mconst от постоянной нагрузки q1 = 20 кН/м – по элементам первого столбца матрицы M(F) (рис. 16.17); 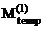 от первой временной нагрузки q2 = 12 кН/м – по элементам второго столбца матрицы M(F) (рис. 16.18);
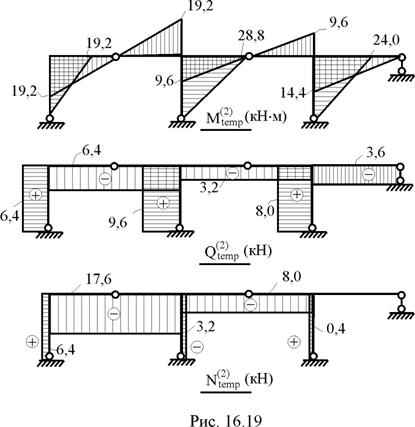
от первой временной нагрузки q2 = 12 кН/м – по элементам второго столбца матрицы M(F) (рис. 16.18); 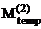 от второй временной нагрузки F = 24 кН – по элементам третьего столбца матрицы M(F) (рис. 16.19).
от второй временной нагрузки F = 24 кН – по элементам третьего столбца матрицы M(F) (рис. 16.19).
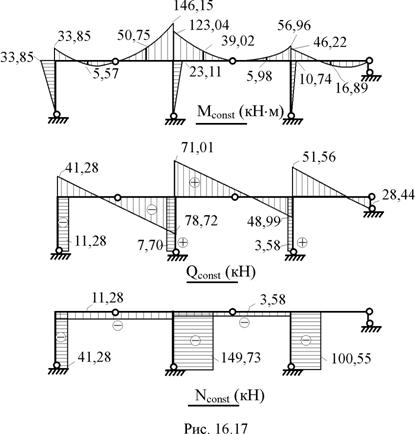
12. Построение эпюр поперечных (Qconst, 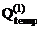 ,
, 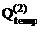 ) и продольных сил (Nconst,
) и продольных сил (Nconst, 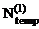 ,
, 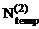 ) от каждого из вышеупомянутых воздействий (рис. 16.17, 16.18, 16.19).
) от каждого из вышеупомянутых воздействий (рис. 16.17, 16.18, 16.19).
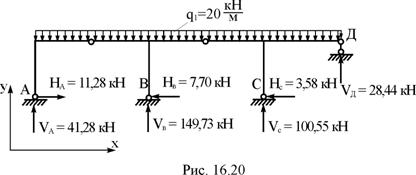
13. Статическая проверка условий равновесия рамы в целом. Здесь эту проверку проведём только в случае действия постоянной нагрузки (рис. 16.20).
åFx = 0, 11,28 – 7,70 – 3,58 = 0, 0 º 0;
åFy = 0, 41,28 + 149,73 + 100,55 + 28,44 – 20×16 = 0, 0 º 0;
åmom(F)B = 0, 41,28×6 – 100,55×6 – 28,44×10 – 20×6×3 +
+ 20×10×5 = 1247,68 – 1247,70 = –0,02.
Относительная погрешность вычислений при проверке последнего условия равновесия составляет
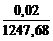 × 100 % = 0,0016 %.
× 100 % = 0,0016 %.
14. Вычисление расчётных изгибающих моментов в характерных сечениях рамы (табл. 2).
Таблица 2
| № сечений | Изгибающие моменты, кН×м | Расчётные изгибающие моменты, кН×м | |||
| Mconst | 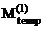 | 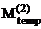 | max | min | |
| -33,85 | 13,61 | 19,2 | -1,04 | -33,85 | |
| -146,15 | -13,61 | -19,2 | -146,15 | -178,96 | |
| -123,04 | -41,21 | 9,6 | -113,44 | -164,25 | |
| -56,96 | -66,8 | -9,6 | -56,96 | -133,36 | |
| -46,22 | -52,8 | 14,4 | -31,82 | -99,02 | |
| 16,89 | -26,4 | 7,2 | 24,09 | -9,51 | |
| 10,74 | 14,0 | 24,0 | 48,74 | 10,74 | |
| 23,11 | -27,61 | 28,8 | 51,91 | -4,50 | |
| -33,85 | 13,61 | 19,2 | -1,04 | -33,85 |
Вопросы для самопроверки
1. Что называется основной системой метода сил?
2. Какие приёмы используются для удаления лишних связей из заданного статически неопределимого сооружения?
3. В каком случае основная система метода сил для заданного статически неопределимого сооружения будет статически определимой?
4. Сформулируйте требования, предъявляемые к основной системе метода сил. Выполнение какого требования является абсолютно обязательным при выборе основной системы?
5. Для заданного преподавателем статически неопределимого сооружения, испытывающего силовое воздействие, запишите в общем виде систему канонических уравнений метода сил, используя статически определимую основную систему. Поясните физический смысл i-го уравнения этой системы.
6. Какой смысл имеют неизвестные метода сил X1, X2, …, Xj, …, Xn?
7. Поясните физический смысл входящих в систему канонических уравнений произведений чисел diiXi и dijXj?
8. Какой физический смысл имеют коэффициенты при неизвестных dii и dij, а также грузовые коэффициенты DiF системы канонических уравнений метода сил? Как определяются эти коэффициенты для плоских стержневых систем в общем случае? Какие упрощения при вычислении коэффициентов dii, dij и DiF имеют место в плоских рамных и балочных системах?
9. Как проверить правильность вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода сил?
10. Каким образом при силовом воздействии вычисляются внутренние усилия в заданном статически неопределимом сооружении, если известны усилия в лишних связях этого сооружения X1, X2, …, Xj, …, Xn: для плоских стержневых систем в общем случае? для плоских рамных и балочных систем?
11. Как производится проверка правильности эпюр внутренних усилий при силовом воздействии, полученных: для произвольной плоской статически неопределимой стержневой системы? для плоской рамной или балочной системы?
12. Запишите в общем виде систему канонических уравнений метода сил в матричной форме, а также матричные соотношения для вычисления элементов: матрицы внешней податливости сооружения d, матрицы грузовых коэффициентов системы канонических уравнений DF, матрицы неизвестных метода сил Х, матрицы внутренних усилий в заданном статически неопределимом сооружении S.
13. Какой смысл имеют элементы матриц L, LF, B, S? Какие блоки (подматрицы) включают в себя матрицы L, LF, B, S?
14. Определите число строк и столбцов в матрицах L, LF, B для конкретной плоской стержневой системы с заданным силовым воздействием.
15. Каким образом проверяется правильность вычисления элементов матрицы внутренних усилий в заданном статически неопределимом сооружении при силовом воздействии?
16.10. Рекомендуемая литература
1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с.
Гл. 6. Метод сил. § 6.1. Основная идея метода сил. § 6.2. Лишние неизвестные. Выбор основной системы метода сил. § 6.3. Канонические уравнения метода сил и их свойства. § 6.4. Вычисление коэффициентов и свободных членов канонических уравнений и их проверка. § 6.5. Построение окончательных эпюр внутренних усилий. Статическая и кинематическая проверки. – С. 124–134. § 6.7. Пример расчета статически неопределимой рамы методом сил. – С. 136–140. § 6.10. Матричная форма метода сил. – С. 149–151.
2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.
Гл. 6. Расчёт статически неопределимых систем методом сил. § 6.2. Канонические уравнения метода сил. § 6.3. Расчёт статически неопределимых систем на действие заданной нагрузки. – С. 199–213. § 6.7. Построение эпюр поперечных и продольных сил. Проверка эпюр. – С. 222–228. § 6.14. Проверка коэффициентов и свободных членов системы канонических уравнений. § 6.15. Примеры расчёта рам. – С. 247–260.
3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.
Гл. XI. Метод сил. § 59. Канонические уравнения и их особенности. § 60. Общий алгоритм расчёта. – С. 316–332. § 64. Расчёт статически неопределимых систем в матричной форме. – С. 368–381.
4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.
Гл. IX. Расчёт рам методом сил. § IX.1. Порядок расчёта рам. – С. 137–145. § IX.7. Расчёт рам в матричной форме. – С. 169–181.
5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с.
Гл. 5. Расчёт сооружений методом сил. § 5.1. Основная идея метода сил. Выбор рациональной основной системы. Примеры 5.1–5.5. – С. 8–15. § 5.2. Силовое воздействие. Примеры 5.12–5.13. – С. 23–35.
6. Проценко В.М. Расчёт статически неопределимых рам: Методические указания / В.М. Проценко, В.Г. Себешев. – Новосибирск: НГАС, 1993. – 56 с.
Задача № 1. Расчёт плоской статически неопределимой рамы методом сил. – С. 1–28.
Лекция пятнадцатая
Теоремы взаимности строительной механики
15.1. Теорема о взаимности возможных работ
15.2. Теорема о взаимности перемещений
15.3. Теорема о взаимности реакций
15.4. Теорема о взаимности реакций и перемещений
15.5. Вопросы для самопроверки
15.6. Рекомендуемая литература
