Начальная и конечная критические нагрузки. Связь расчетного сопротивления грунта с начальной критической нагрузкой.
Начальная критическая нагрузка р*
Соответствует случаю, когда в единственной точке в основании под краем ленточного фундамента возникает предельное состояние. Для определения р* рассмотрим простейший случай, когда основание неводонасыщенное, линейно-деформируемое, однородное и изотропное, а напряжение от собственного веса грунта распределяется по закону гидростатики, т.е.:
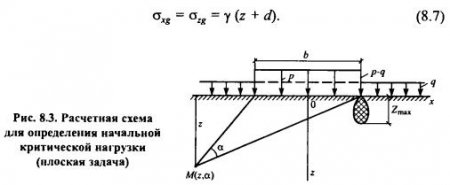
Распределение напряжений в рассматриваемом грунтовом массиве при z>0 в любой точке M (z, α) можно определить от собственного веса грунта следующим образом:
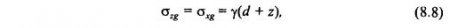
где d - глубина от дневной поверхности, γ - удельный вес грунта. Это означает, что напряжения σzg и σxg являются главными.
Максимальные и минимальные главные напряжения от действия полосовой нагрузки р-q на ширину b можно определить по известным соотношениям, т. е.:
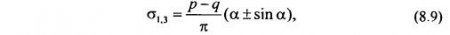
где α - угол видимости.
Суммарное значение главных напряжений в любой точке можно определить таким образом:
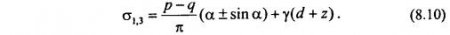
Предельное напряженное состояние в точке M(z, а) может реализоваться, если напряжения (8.10) будут удовлетворять условию предельного состояния:
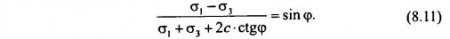
Подставляя σ1,3 из (8.10) в (8.11), получим:
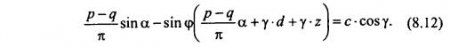
Уравнение (8.10) представляет собой геометрическое место точек, где выполняется условие (8.11). Координаты этих точек z и α можно получить, решая (8.12) относительно z, т. е.:
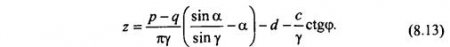
Это уравнение кривой очертания области предельного равновесия и имеет максимальную ординату zmax (рис. 8.3) в зависимости от р. Ее можно найти, взяв производную dz/dα и приравняв ее нулю, т. е.:
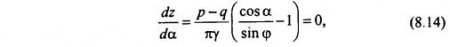
отсюда следует, что z = zmax, когда cosα = sinφ, т. е. α = п/2-φ и sinα = соsφ.
Тогда, подставив это выражение в (8.13), получим максимальное значение z в виде:
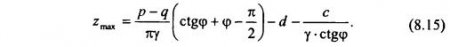
Отсюда легко определить максимальную ординату области предельного равновесия в зависимости от заданного значения граничной нагрузки р.
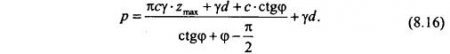
Полагая Zmax = 0, получим значения начальной критической нагрузки, т. е. имеем:
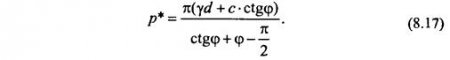
Это выражение без учета сцепления грунта было впервые получено Н.П. Пузыревским. Для случаев отсутствия трения (φ = 0, с ≠ 0), к которым можно отнести жирные глины и слабые водонасыщенные глины в нестабилизированном состоянии уплотнения, получим:
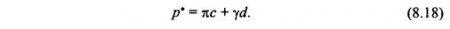
Начальная критическая нагрузка является совершенно безопасной для грунтового основания. Однако при этом не полностью используются резервы несущей способности основания. Поэтому полагают, что расширение области предельного равновесия на глубину Zmax = b/4 несущественно влияет на несущую способность основания, а зависимость осадки от нагрузки при этом остается линейной. Следовательно, для определения осадок основания при р<р* можно использовать аппарат теории упругости.
Подставляя zmax = b/4 в (8.16), получим так называемое нормативное сопротивление грунта:
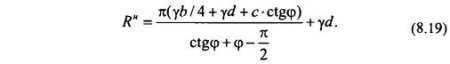
Это выражение можно представить в виде трехчленной формулы:
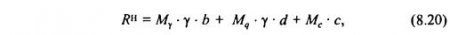
где Mγ, Mq, Mc- безразмерные коэффициенты, зависящие от угла внутреннего трения φ, и вычисляются по формулам:
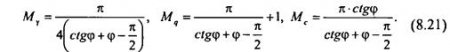
Опыт использования формулы (8.21) и наблюдения за осадками сооружения позволили еще больше увеличить диапазон между р* и Rн - последнее получило название расчетного сопротивления грунта основания Rр и рекомендуется СНиП 2.02.01-83 и определяется выражением вида:
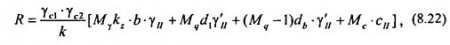
где γс1, γс2 - коэффициенты условий работы, принимаемые по таблицам СНиП; к - коэффициент надежности, принимаемый равным 1, если прочностные характеристики грунта φII и сII определены непосредственно по результатам испытания, и равным 1,1, если они приняты по справочным таблицам; Mγ, Mq, Mc - коэффициенты, определяемые по (8.21) и принимаемые по СНиП; kz-коэффициент, принимаемый равным 1 при ширине подошвы фундамента b≤10 м, а при b≥10 м - kz = Z0/b + 0,2, где Z0 = 8 м; b - ширина подошвы фундамента (м), γII - удельный вес грунтов, залегающих ниже подошвы фундамента (кН/м3); γ’II - удельный вес грунтов, залегающих выше подошвы фундамента; - приведенная глубина заложения наружных и внутренних фундаментов от пола подвала:
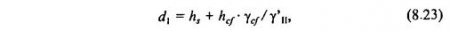
где hs - толщина слоя грунта выше подошвы фундамента со стороны подвала (м); hcf - толщина пола подвала (м); γcf - расчетный удельный вес материала пола подвала; db - глубина подвала, равная от уровня планирования до пола подвала (м); для сооружений с подвалом шириной В≤20 м и глубиной более 2 м принимается db = 2 м, при ширине подвала В≥20 м принимается db = 0; сII - расчетное сцепление несущего слоя грунта.
В заключение отметим, что расчет осадки оснований сооружений при условии, когда среднее давление р под подошвой фундамента не превышает R, при ширине фундамента более 10 м практически выполняется всегда. Поэтому проверка условия р≤R для плитных фундаментов размером 20x30, 40x50, а иногда и 100x100 является бессмысленной. В таких случаях целесообразно пользоваться другим решением, исключающим ширину фундамента из формулы для определения расчетного сопротивления.
Предельная критическая нагрузка p**
При действии р** в грунтах основания полностью формируются области предельного состояния, грунты теряют свою несущую способность и развивается незатухающая провальная осадка, сопровождаемая выпором грунта в стороны, а также на поверхность в случае неглубокого заложения фундамента (рис. 8.1, б). Такое состояние абсолютно недопустимо для любого сооружения.
Для количественной оценки р** необходимо решить соответствующую задачу теории пластичности. Впервые это удалось сделать Л. Прадтлю и Г. Рейснеру в предположении отсутствия сил собственного веса грунта, т. е. γ = 0. Это решение имеет вид:
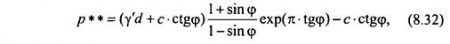
где γ' - удельный вес грунта выше оси у; d - глубина от поверхности до оси у.
Расчетная схема этой задачи представлена на рис. 8.5, на котором представлены границы одной из областей предельного равновесия и два семейства линий скольжения, соответствующие этому решению.
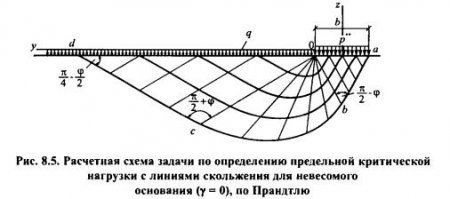
Линии скольжения в центральной части под загруженной площадью образуют ромбы под углом п/2 - φ (зона аов). В сегменте овс семейство линий скольжения имеют веерообразную форму, которая ограничивается отрезком ос логарифмических спиралей. Наконец, третья зона (ocd) образована ромбами, но вытянутыми вдоль оси х под углом п/4 - φ/2.
Для идеально связанных грунтов (φ = 0; с ≠ 0) решение (8.32), для случая плоской задачи, примет вид:
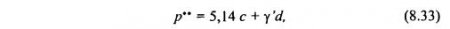
а для случая осесимметричной задачи - следующий вид:
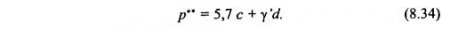
Сравнивая эти значения р** с начальной критической нагрузкой р* (8.20), видим, что они отличаются почти в 2 раза.
Недостаток этой теории заключается в том, что не учитывается собственный вес грунта и свойство подстилающего грунта. Экспериментальные исследования показали, что эти обстоятельства приводят к занижению р**. Решение Л. Прандтля было далее рассмотрено и развито К. Терцаги, В.Г. Березанцевым, М.В. Малышевым, с учетом формы и размеров уплотненного ядра под подошвой фундамента.
Решение этой задачи для нафузки, приложенной под определенным углом δ, было рассмотрено В.В. Соколовским.
Эти решения справедливы при относительно небольших глубинах заложения фундаментов и однородном строении основания. Очевидно, что наличие жесткого подстилающего слоя окажет существенное влияние на р**. Очевидно также, что при заглубленных фундаментах типа буровых опор и свай, механизм развития зон предельного состояния и, следовательно, предельное значение нагрузки на сваи следует определить исходя из других расчетных схем.
