Матрицы смежности и инцидентности

На рис 3.12 изображено множество точек V и множество линий E, соединяющих эти точки, которые все вместе образуют граф Г. Если линии имеют стрелки, то граф называется ориентированным или орграфом Г₀ (рис. 3.13). Внутренних различий между Г и Г₀ гораздо меньше, чем между графом, изображающим правильную решетку из подгрупп для какой-нибудь группы, например,S( 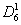) (рис. 2.18), и графом, изображающим сильно неправильную метарешетку M₁₆ (рис. 2.26).

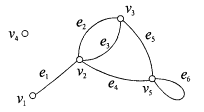
Рис. 3.12

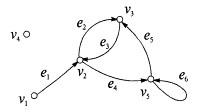
Рис. 3.13

Внешняя морфология графа (со стрелками или без них) играет подчиненную роль, математическая же сущность представленного графом объекта всегда остается где-то за рамками рисунка. Изображение графа в большинстве случаев является проекцией или тенью этой сущности и самостоятельного значения не имеет. Однако морфология расположения точек и линий, тем не менее, поддается определенной математической классификации и описанию. Этим мы намерены заняться в этом и последующем подразделах.

Линии в графе Г здесь и далее будем называть ребрами, а ориентированные линии в орграфе Г₀ — дугами. О вершинах и ребрах (дугах) говорят, что они инцидентны, если вершина принадлежит ребру (дуге); если вершина не инцидентна никакому ребру (дуге), то она называется изолированной (v₄). Путь называется простым, если никакая дуга или ребро не встречается в нем дважды. Путь называется элементарным, если никакая вершина в нем не встречается дважды.

Цикл — это замкнутый путь в неориентированном графе. Контур — это ориентированный цикл в орграфе. Понятия простоты и элементарности распространяются на циклы и контуры. Контур или цикл, который содержит все ребра или дуги графа, называется эйлеровым. Можно показать, что связанный орграф (т.е. без изолированных фрагментов) содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих; связанный неориентированный граф содержит эйлеров цикл тогда и только тогда, когда степень каждой вершины четна. Степенью (валентностью) вершины называется число инцидентных ей ребер. Простой путь, который проходит через все вершины графа, называется гамильтоновым. Если в простом графе с n вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым. Однако легко построить гамильтонов граф, у которого степень вершины меньше n/2.

Графы Г и Г₀ можно представить в аналитической форме либо матрицей смежности A, либо матрицей инцидентности B. Для нашего конкретного неориентированного графа Г матрицы A и B выглядят следующим образом:

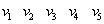A(Г) =	B(Г) =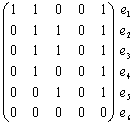

Матрица смежности для неориентированного графа всегда симметрична. Фигурирующая в ней 2 может быть в некоторых случаях заменена на 1. В матрице инцидентности сумма единиц по столбцам указывает на степень вершины v_i. Нередко расположение вершин и ребер в этой матрице меняют местами (транспонируют). Так, для нашего конкретного орграфа Г₀ матрица A и B выглядят иначе:

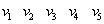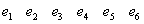A(Г0 ) =	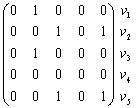B(Г0 ) =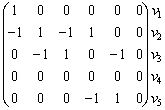

Пути в графе

Путь в графе — последовательность вершин, имеющая для каждой вершины ребро, соединяющее её со следующей вершиной в последовательности.

Два пути вершинно независимы, если они не имеют общих внутренних вершин. Аналогично два пути рёберно независимы, если они не имеют общих внутренних рёбер.

Длина пути — это число рёбер, используемых в пути, при этом многократно используемые рёбра считаются соответствующее число раз. Длина может равняться нулю, если путь состоит из одной только вершины.

Взвешенный граф ставит в соответствие каждому ребру некоторое значение (вес ребра). Весом пути во взвешенном графе называется сумма весов рёбер пути. Иногда вместо слова вес употребляется цена или длина.

Пустые и полные подграфы

Пусть имеется граф G, обладающий свойствомP. Будем говорить, что графG являетсяP-минимальным, если не существует подграфа 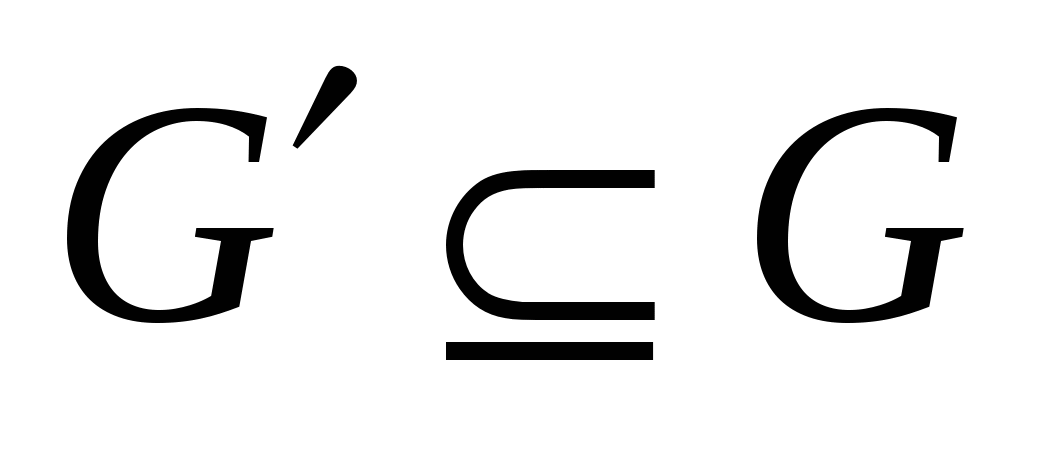, обладающего этим свойством. ГрафG называетсяP-максимальным, если не существует надграфа 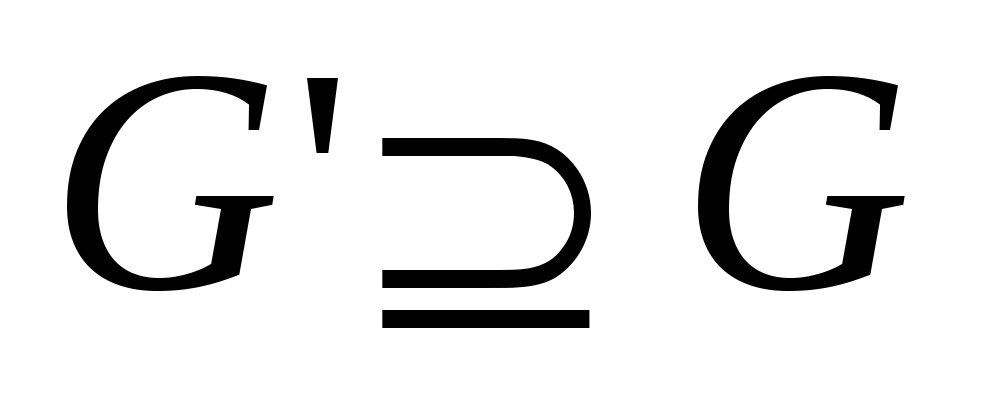, который обладает свойствомP. Например, на данном множестве вершин дерево является минимальным связным и максимальным графом без циклов. Слова «наибольший» и «наименьший» будем использовать для обозначения части графа, обладающей свойствомPи имеющей наибольшую (наименьшую) мощность.

Сети

Сетью называется граф, элементам которого поставлены в соответствие некоторые параметры. Далее элементы множества R будем называть узлами, а множества 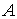– дугами. Пусть каждой дуге 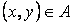некоторой сети 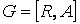поставлено в соответствие неотрицательное (действительное) число 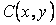, называемое пропускной способностью дуги 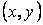. Функция 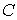, отображающая множество 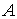в множество неотрицательных чисел, называется функцией пропускной способности. Пусть s и t – два различных узла из R. Стационарный поток величиныv из s в t в сети 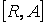есть функция f, отображающая множество А в множество неотрицательных чисел, удовлетворяющая линейным уравнениям и неравенствам

Раскраска графов

В теории графов, раскраска графов является частным случаем разметки графов. При раскраске элементам графа ставятся в соответствие метки с учетом определенных ограничений; эти метки традиционно называются “цветами”. В простейшем случае, такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называетсяраскраской вершин. Аналогично, раскраска ребер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета.^[1] Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

Раскраска вершин – главная проблема раскраски графов, все остальные задачи в этой области могут быть перенесены на эту модель. Например, раскраска ребер графа - это раскраска вершин его рёберного графа, а раскраска областей планарного графа – это раскраска вершин двойственного графа.^[1] Тем не менее, другие проблемы раскраски графов часто ставятся и решаются в изначальной постановке. Причина этого частично заключается в том, что это даёт лучшее представление о происходящем и более показательно, а частично из-за того, что некоторые задачи таким образом решать удобнее (например, раскраска ребер).

Договоренность об использовании цветов происходит из традиции выделения цветом стран на политической карте.^[1] Она была обобщена на окраску областей планарного графа. Через двойственные графы эта модель распространилась и на раскраску вершин, а затем и на другие виды графов. В математическом и компьютерном представлении обычно в качестве цветов используются целые неотрицательные числа (от нуля и больше). Таким образом, мы можем использовать любой конечный набор в качестве “цветового набора”, и проблема раскраски графов зависит от количества цветов, а не от того, чем они являются.

Дискретная математика

Теория множеств

Понятие множества является исходным не определяемым строго понятием. Приведем здесь определение множества (точнее, пояснение идеи множества), принадлежащее Г. Кантору: "Под многообразием или множеством я понимаю вообще все многое, которое возможно мыслить как единое, т.е. такую совокупность определенных элементов, которая посредством одного закона может быть соединена в одно целое".

Множества будем, как правило, обозначать большими буквами латинского алфавита, а их элементы — малыми, хотя иногда от этого соглашения придется отступать, так как элементами некоторого множества могут быть другие множества. Тот факт, что элемент а принадлежит множеству 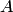, записывается в виде .

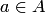В математике мы имеем дело с самыми различными множествами. Для элементов этих множеств мы используем два основных вида обозначений: константы и переменные.

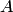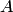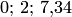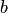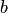Индивидная константа (или просто константа) с областью значений обозначает фиксированный элемент множества . Таковы, например, обозначения (записи в определенной системе счисления) действительных чисел: . Для двух констант и с областью значений 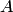будем писать 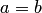, понимая под этим совпадение обозначаемых ими элементов множества .

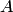Индивидное переменное (или просто переменное) с областью значений 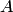обозначает произвольный, заранее не определенный элемент множества 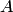. При этом говорят, что переменное 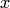пробегает множество 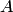или переменное 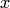принимает произвольные значения на множестве 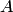. Можно фиксировать значение переменного 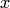, записав , где — константа с той же областью значений, что и 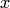. В этом случае говорят, что вместо переменного 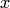подставлено его конкретное значение , или произведена подстановка вместо 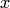, или переменное 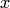приняло значение .

Равенство переменных 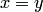понимается так: всякий раз, когда переменное 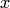принимает произвольное значение , переменное 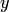принимает то же самое значение , и наоборот. Таким образом, равные переменные "синхронно" принимают всегда одни и те же значения.

Обычно константы и переменные, область значений которых есть некоторое числовое множество, а именно одно из множеств 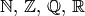и 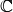, называют соответственно натуральными, целыми (или целочисленными), рациональными, действительными и комплексными константами и переменными. В курсе дискретной математики мы будем использовать различные константы и переменные, область значений которых не всегда является числовым множеством.

Для сокращения записи мы будем пользоваться логической символикой, позволяющей коротко, наподобие формул, записывать высказывания. Понятие высказывания не определяется. Указывается только, что всякое высказывание может быть истинным или ложным (разумеется, не одновременно!).

Отношения

Подмножество называется местным (мерным) отношением на множестве А. Говорят, что элементы находятся в отношении , если .

Одноместное (одномерное) отношение — это просто некоторое подмножество А. Такие отношения называют признаками. Говорят, что обладает признаком , если и . Свойства одноместных отношений — это свойства подмножеств А, поэтому для случая термин “отношения” употребляется редко.

Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения. Если и находятся в отношении , это обычно записывается в виде .

Пример 1. Бинарные отношения на множестве .

а) Отношение “” выполняется для пар и не выполняется для пары .

б) Отношение “иметь общий делитель, не равный единице” выполняется для пар и не выполняется для пар .

в) Отношение “быть делителем” выполняется для пар и не выполняется для пар .

Пример 2. Бинарные отношения на множестве точек координатной плоскости.

а) Отношение “быть равноудалёнными от начала координат” выполнятся для пар точек и , но не выполнятся для пары точек и .

б) Отношение “принадлежать окружности, центр которой находится в начале координат”, выполняется для первой пары точек из предыдущего примера и не выполняется для второй пары.

в) Отношение “быть удалёнными на разное расстояние от начала координат” выполняется для всех точек, для которых не выполняется отношение, описанное в пункте “б”.

Пусть дано отношение на множестве А. Для любого подмножества определяется отношение , называемое сужением на , которое получается из отношения удалением всех пар, содержащих элементы, не принадлежащие . Иначе говоря, .

Строго говоря, само отношение и его сужение - это разные отношения, с разными областями определения. Однако, по умолчанию, если не возникает явных разночтений, эта разница не учитывается. Например, вполне можно говорить об отношении “быть делителем”, не уточняя, задано оно на множестве или на каком-нибудь его подмножестве.

Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется). Отношения на конечных множествах обычно задаются списком или матрицей. Матрица бинарного отношения на конечном множестве - это квадратная матрица порядка , в которой каждый элемент определяется следующим образом:

Моделирование

Понятие моделирование

Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.

Под моделью понимается физический или абстрактный объект, свойства которого в определенном смысле сходны со свойствами исследуемого объекта. При этом требования к модели определяются решаемой задачей и имеющимися средствами [19]. Существует ряд общих требований к моделям:

1. Адекватность – достаточно точное отображение свойств объекта;
2. Полнота – предоставление получателю всей необходимой информации об объекте;
3. Гибкость – возможность воспроизведения различных ситуаций во всем диапазоне изменения условий и параметров;
4. Трудоемкость разработки должна быть приемлемой для имеющегося времени и программных средств.

Моделирование – это процесс построения модели объекта и исследования его свойств путем исследования модели.

Классификация моделей

Признаки классификаций моделей: 1) по области использования;

2) по фактору времени;

3) по отрасли знаний;

4) по форме представления

1) Классификация моделей по области использования:

Учебные модели – используются при обучении;

Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик

Научно - технические - создаются для исследования процессов и явлений

Игровые – репетиция поведения объекта в различных условиях

Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок)

2) Классификация моделей по фактору времени:

Статические – модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Примеры моделей: классификация животных…., строение молекул, список посаженных деревьев, отчет об обследовании состояния зубов в школе и тд.

Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.

3) Классификация моделей по отрасли знаний- это классификация по отрасли деятельности человека: Математические, биологические, химические, социальные, экономические, исторические и тд

4) Классификация моделей по форме представления:

Материальные– это предметные (физические) модели. Они всегда имеют реальное воплощение. Отражают внешнее свойство и внутреннее устройство исходных объектов, суть процессов и явлений объекта-оригинала. Это экспериментальный метод познания окружающей среды.Примеры: детские игрушки, скелет человека, чучело, макет солнечной системы, школьные пособия, физические и химические опыты

Абстрактные (нематериальные) – не имеют реального воплощения. Их основу составляет информация. это теоретический метод познания окружающей среды. По признаку реализации они бывают: мысленные и вербальные; информационные

Мысленныемодели формируются в воображении человека в результате раздумий, умозаключений, иногда в виде некоторого образа. Это модель сопутствует сознательной деятельности человека.

Вербальные– мысленные модели выраженные в разговорной форме. Используется для передачи мыслей

Информационные модели – целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойств этого объекта.

Типы информационных моделей :

Табличные – объекты и их свойства представлены в виде списка, а их значения размещаются в ячейках прямоугольной формы. Перечень однотипных объектов размещен в первом столбце (или строке), а значения их свойств размещаются в следующих столбцах (или строках)

Иерархические – объекты распределены по уровням. Каждый элемент высокого уровня состоит из элементов нижнего уровня, а элемент нижнего уровня может входить в состав только одного элемента более высокого уровня

Сетевые – применяют для отражения систем, в которых связи между элементами имеют сложную структуру

По степени формализацииинформационные модели бывают образно-знаковые и знаковые. Напримеры:

Образно-знаковые модели :

Геометрические (рисунок, пиктограмма, чертеж, карта, план, объемное изображение)

Структурные (таблица, граф, схема, диаграмма)

Словесные (описание естественными языками)

Алгоритмические (нумерованный список, пошаговое перечисление, блок-схема)

Знаковые модели:

Математические – представлены матем.формулами, отображающими связь параметров

Специальные – представлены на спец. языках (ноты, хим.формулы)

Алгоритмические – программы

Признаки классификаций моделей:Классификация моделей по области использования