Определение количественных характеристик надежности

По статистическим данным об отказах изделия

Количественная оценка надёжности позволяет производить расчет надёжности, сформулировать требования, предъявляемые к надёжности вновь разрабатываемых систем, заранее рассчитать срок службы трубопроводов, оборудования и т.д., составить плановое задание по уходу за системой, ее ремонтом и восстановлением.

Любые показатели (или формы количественного представления), определяющие безотказность, основываются на теоретическом или статистическом определении функции распределения времени безотказной работы, которая показывает вероятность того, что на отрезке времени [0, t] не произойдет отказ рассматриваемого объекта (трубопровода), имеющего наработку X:

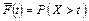
Физический смысл.

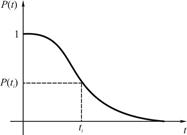
Величина Р(t_i) характеризует долю работоспособных изделий к моменту времени t_i.

Рис. 1. Кривая распределения вероятности

безотказной работы

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением

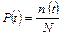(1)

где n(t) – число изделий, неотказавших к моменту времени t; N – число изделий, поставленных на испытания; Р(t) – статистическая оценка вероятности безотказной работы изделия. Типичный график функции Р(t) представлен на рис. 1 и называется в специальной литературе «кривой убыли».

Для вероятности отказа по статистическим данным справедливо соотношение 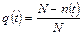(2)

(2)

где N–n(t) – число изделий, отказавших к моменту времени t; Р (t) – статистическая оценка вероятности отказа изделия.

Частота отказов по статистическим данным об отказах определяется выражением

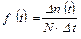(3)

где Δn(t) – число отказавших изделий на участке времени (t, t+Δt); f(t) – статистическая оценка частоты отказов изделия; Δt – интервал времени.

Большинство современных исследований надежности систем водоснабжения и водоотведения в качестве показателей безотказности используют вероятность безотказной работы или производный от него показатель – интенсивность отказов λ(t):

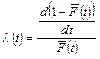
Физический смысл интенсивности отказов – это мера, выражающая склонность объекта к отказу в зависимости от времени его эксплуатации.

Интенсивность отказов (условная плотность вероятности отказов) по статистическим данным об отказах определяется формулой:

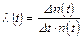(4)

где n(t) – число изделий, не отказавших к моменту времени t; Δn(t) – число отказавших изделий на участке времени (t, t+Δt); λ (t) – статистическая оценка интенсивности отказов изделия.

Для решения задач о прогнозировании работоспособности необходима математическая модель, которая должна быть представлена аналитическим выражением интенсивности отказов λ(t). Типичная кривая распределения отказов представлена на рис. 2. Вероятность безотказной работы и интенсивность отказов являются функциями времени формулы (1), (4). Причем, вероятность безотказной работы – всегда убывающая функция, (рис. 1), а интенсивность отказов может быть как возрастающей функцией, так и неизменной (рис. 2).

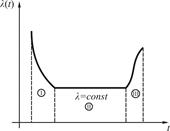Кривую изменения отказов можно условно разделить на три характерных участка:

первый (I) – период приработки,

второй (II) – период нормальной эксплуатации,

третий (III) – период старения объекта.

Рис. 2. Кривая изменения интенсивности отказов

во времени

Отказы, появляющиеся в периоде нормальной эксплуатации, называют внезапными, так как они появляются в случайные моменты времени, т.е. внезапно, непредсказуемо.

Интенсивность отказов постоянна тогда и только тогда, когда функция распределения наработки F(t) = 1– F (t) распределена по экспоненциальному закону.

Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Среднее время безотказной работы оборудования (средняя наработка до первого отказа) по статистическим данным оценивается выражением

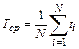(5)

где t_i – время безотказной работы i-го изделия; N – общее число изделий, поставленных на испытания; Т_ср – статистическая оценка среднего времени безотказной работы изделия.

Для определения Т_ср по формуле (5) необходимо знать моменты выхода из строя всех N изделий. Можно определять Т_ср из уравнения

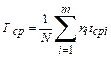(6)

где n_i – количество вышедших из строя изделий в i-ом интервале времени; t_ср.i = (t_i-1+t_i)/2; m=t_k/Δt; Δt=t_i+1–t_i; t_i–1 – время начала i-го интервала; t_i – время конца i-го интервала; t_k – время, в течение которого вышли из строя все изделия; Δt – интервал времени.

Дисперсия времени безотказной работы изделия по статистическим данным определяется формулой

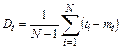(7)

где D_t – статистическая оценка дисперсии времени безотказной работы изделия.

Задача 1.

На испытании находилось N₀ = 100 образцов неремонтируемого оборудования. Число отказов оборудования n (Dt) фиксировалось через каждые 200 часов работы. Данные об отказах оборудования приведены в табл. 1. По этим опытным данным вычислить количественные показатели надежности:

1. Р(t) – вероятность безотказной работы за время t;

2. f (t) – частота отказов за время t;

3. l (t) – интенсивность отказов за время t;

4. T_ср – средняя наработка до первого отказа, час.

Построить графики зависимостей этих характеристик от времени

Таблица 1

Dt, час	0-	200-	400-	600-	800-	1000-	1200-1400
n (Dti)

Продолжение табл.1

Dt, час	1400-	1600-	1800-	2000-	2200-	2400-
n (Dti)

Продолжение табл. 1

Dti ,час	2600-	2800-
n (Dti))

Задача 2.

Построить график распределения случайной величины, числа снижений (ниже допустимого) объёма подачи воды некоторому потребителю, т.е. число отказов. Наблюдения велись в течение 20 лет. Результаты наблюдений представлены в табл. 2.

Таблица 2

Годы наблюдений
Число отказов в год

Продолжение табл. 2

Годы наблюдений
Число отказов в год

Задача 3.

В течение некоторого времени проводилось наблюдение за работой N₀ экземпляров восстанавливаемых изделий. Каждый из образцов проработал t_i часов и имел n_i отказов. Требуется определить среднюю наработку на отказ по данным наблюдения за работой всех изделий. Исходные данные для расчета приведены в табл. 3.

Таблица 3

вари- ант	Исходные данные
n1	t1, ч.	n2	t2,ч.	n3	t3, ч.	n4	t4, ч.	n5	t5, ч.
							–	–	–	–
									–	–
							–	–	–	–
									–	–
									–	–
									–	–
							–	–	–	–