Расчет закрытой цилиндрической передачи

Определяем межосевое расстояние:

Из условия контактной прочности определяем межосевое расстояние передачи

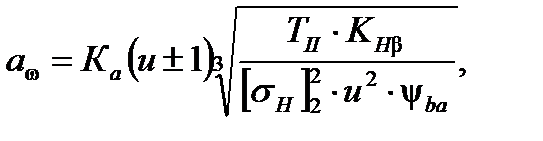
где К_а - коэффициент межосевого расстояния,К_а = 495 МПа - для прямозубых колес;

ψ_ba - коэффициент ширины колесаb₂относительно межосево­го расстояния a_ω;

К_Hβ - коэффици­ент неравномерности распределения нагрузки по длине контактной ли­нии.

ψ_bd – допускаемое контактное напряжение передачи, МПа.

ψ_bd= ψ_ba(u + 1)/2=0,4∙(5+1)/2=1,2

тогда принимаем исходя из [табл. 3.5] К_Hβ = 1,07

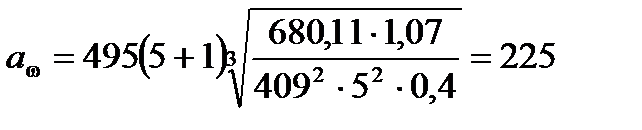, мм.

Для прямозубых колес модуль зацепления рас­считываем по выражению

m= (0,01...0,02)а_w, мм,

m= (0,01...0,02)∙225=2,25…4,5;

Принимаем стандартный нормальный модуль m=3мм.

Определение числа зубьев:

Суммарное число зубьев z_c определяем по формуле:

,

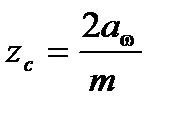где 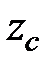– суммарное число зубьев,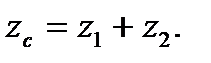

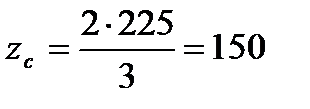
Затем вычисляем число зубьев шестерни z₁ и колеса z₂:

.

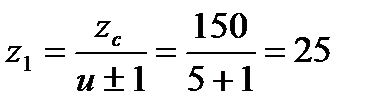
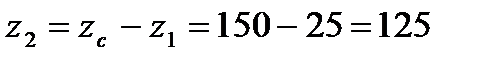Уточняем передаточное отношение:

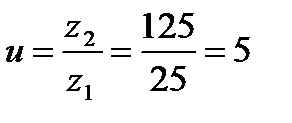
Таблица 2 - Основные параметры передач внешнего зацепления с цилиндрическими прямозубыми колесами.

Геометрические параметры	Расчетные формулы для прямозубых колес
Диаметр делительный окружности d, мм:
шестерни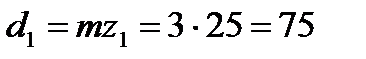
колеса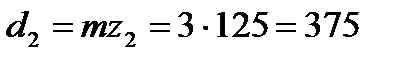
Диаметр окружности выступов da, мм
шестерни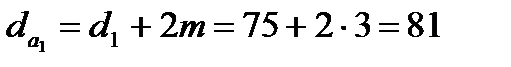
колеса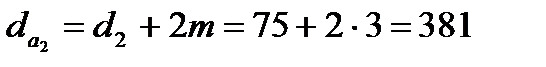
Диаметр окружности впадин df ,мм
шестерни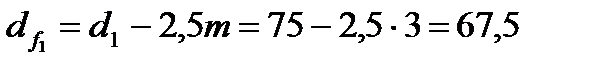
колеса Уточняем Межосевое расстояние аω, мм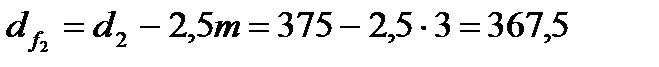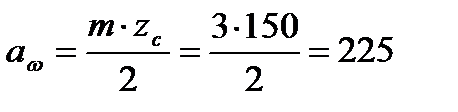
Ширина зуба b, мм
шестерни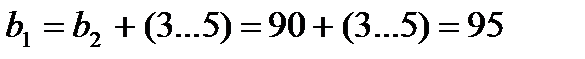
колеса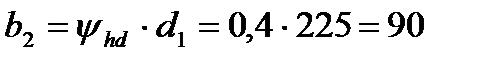

Окружная скорость колес:

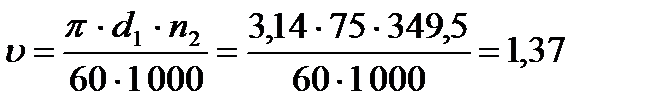м/с.

Проверяем расчет закрытой цилиндрической зубчатой передачи:

Расчет сил в зацеплении:

Окружные: 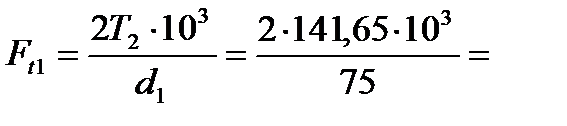3777 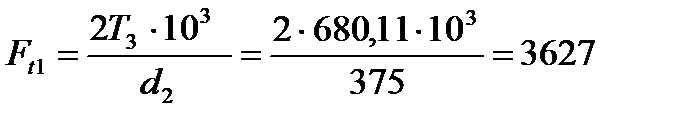Н;

Н;

Радиальные: 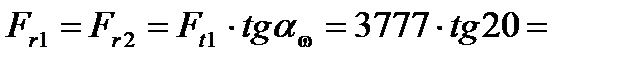1375 Н;

Осевое усилие: ;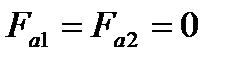

Проверяем передачи по условию контактной прочности:

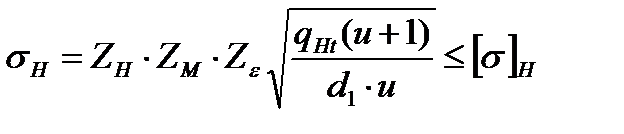
где Z_H =1,76 коэффициент, учитывающий форму сопряженных зубьев,

Z_M - коэффициент, учитывающий механические свойства материалов сопряженных колес,

Z_M = 275 МПа^1/2;

Z _ε - коэффициент, учитывающий суммарную длину контактной линии для прямозубых колес

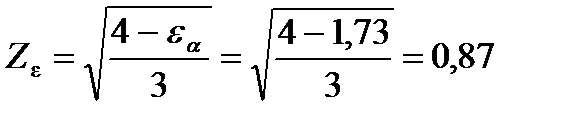
где 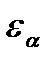-коэффициент торцевого перекрытия

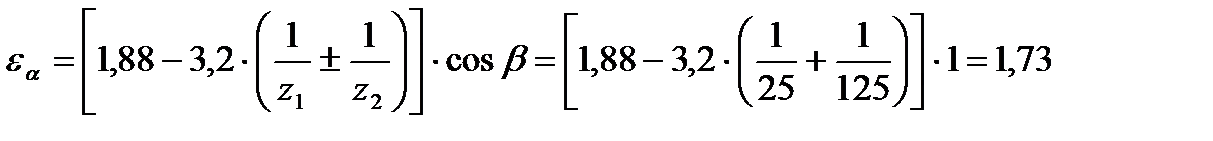
где q_Ht - удельная расчетная окружная сила

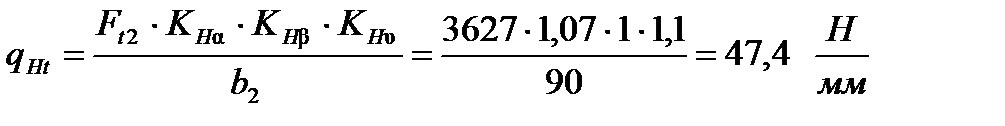
где 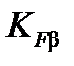- коэффициент неравномерности распределения на грузки по длине зуба при изгибе,

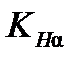- коэффициент неравномерности распределения нагрузки между отдельными зубьями, для прямозубых передач ,

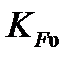- коэффициент динамической нагрузки, который зависит от твердости материала колес, их скорости т степени изготовления,

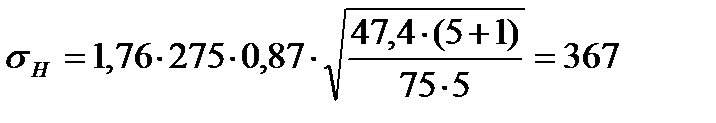МПа,

Перегрузка передачи по контактным напряжениям составляет величину:

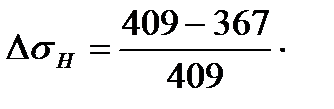100 % = 10,3 %,

Это не выходит за пределы нормы- максимальная перегрузка не должна превышать 20%.

Вычисляем напряжения изгиба у ножки зуба:

Зубья шестерни и колеса буду иметь равную прочность на изгиб при следующем условии

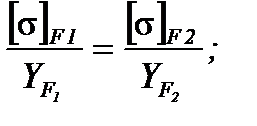
Проверка зубьев на изгибную прочность:

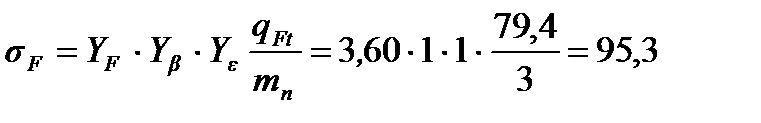МПа,

где Y_F - коэффициент формы зуба, (для шестерни 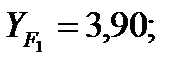для колеса 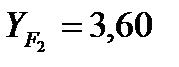[табл. 3.11];

Y_β- коэффициент, учитывающий наклон зубьев

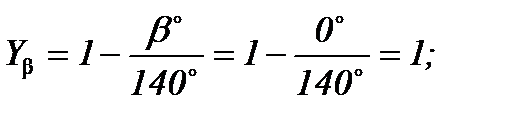
где Y_ε – коэффициент, учитывающий перекрытие зубьев;

q_Ft - удельная расчетная окружная сила

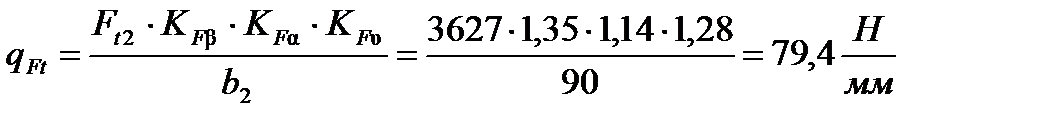
где 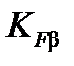- коэффициент неравномерности распределения на грузки по длине зуба при изгибе, принимаем его исходя из [табл. 3,9]

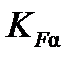- коэффициент неравномерности распределения нагрузки между отдельными зубьями, для прямозубых передач , принимаем его исходя из [табл. 3,9]

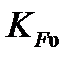- коэффициент динамической нагрузки, который зависит от твердости материала колес, их скорости т степени изготовления, принимаем его исходя из [табл. 3,10]

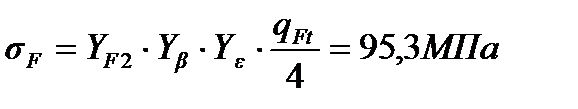
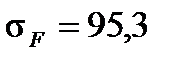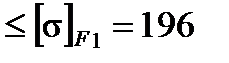Таким образом, полученные в результате расчета изгибные напряжения значительно меньше допускаемых ( МПа МПа).

Расчет на изгиб выполнен для наиболее слабого звена - колеса, т. к. у нее отношение 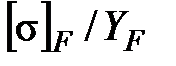меньше, чем у шестерни

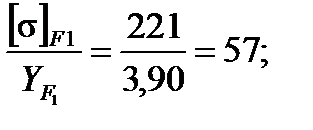
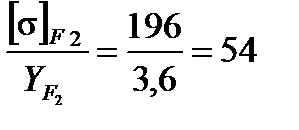
Полученные результаты показали, что спроектированная передача удовлетворяет условиям работоспособности.