Операции над нечёткими множествами

Лекция №3

Тема лекции:Нечёткие множества.

Содержание:

1. Нечёткость.

2. Определения нечётких множеств.

3. Свойства нечётких множеств.

4. Операции над нечёткими множествами.

5. Универсальность нечётких множеств.

Нечёткость, неопределённость

Два вида неопределённости:

· Возникающая из вероятностного поведения системы;

· Связанная с нечёткостью восприятия и обсуждений.

Формализачия второго подхода осуществлена Лотфи Заде (Lotfi Zadeh) в 1965 г. В работе «Fuzzy Sets».

С 1975 г. – теория нечётких множеств в основе нечёткие высказывания-правила «Если-то»

Определение нечётких множеств.

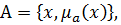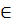Нечёткое множество А в Х есть совокупность упорядоченных пар где х Х, а 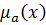- степень принадлежности х к А, т.е. 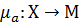- функция отображающая Х в пространстве М – пространство принадлежности.

Определение Заде:

« Нечёткое подмножество А универсального множества U характеризуется функцией принадлежности 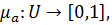которая ставит в соответствии каждому элементу u 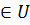число 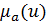из множества [0,1], характеризующее степень принадлежности элемента u множеству А»

Расплывчатое множество А не смотря на нечёткость своих границ может быть точно определенно путём сопоставления каждому объекту х числа, лежащего между 0 и 1, которое представляет его степень принадлежности к А.

Виды записи нечётких множеств

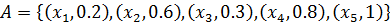
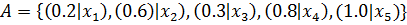
x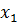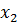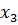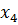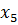
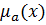	0.2	0.6	0.3	0.8	1.0

Пример нечёткого множества.

«Высокие люди»

Высокий человек – более 2м.

Низкий человек – ниже 1.7 м.

Функция принадлежности «высокие люди»

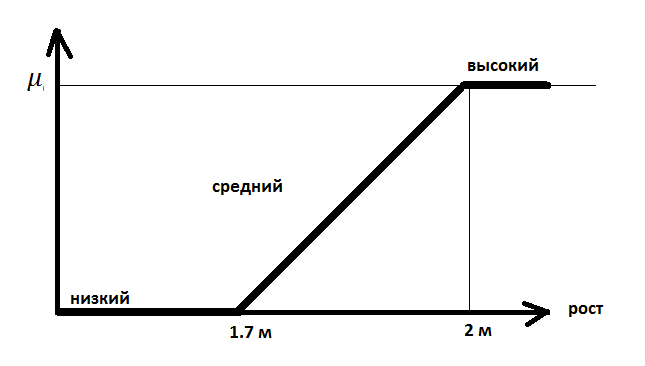
Свойства нечётких множеств

Определение 1.Множество, которое содержит один единственный элемент, называется синглетоном. Синглетон может определяться как среди чётких, так и среди нечётких множеств.

Определение 2.Носителем нечёткого множества А называется множество точек в U, для которых величина 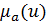положительна. 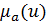>0

Определение 3.Высотой нечёткого множества А называется величина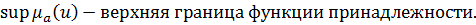

Определение 4.Точкой перехода нечёткого множества А называется такой элемент множества U, степень принадлежности которого множеству А равна 0,5.

Определение 5.Ядром нечёткого множества называется чёткое подмножество универсального множества, элементы которого имеют степени принадлежности равные единице: {x: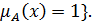

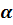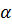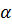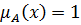
Определение 6. –сечением (или множеством – уровня) нечёткого множества называется чёткое подмножество множества А, элементы котрого имеют степени принадлежности большие или равные : 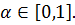Значение 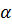называют 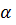– уровнем. Носитель (ядро) можно рассматривать как сечение нечёткого множества на нулевом (единичном) 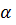- уровне.

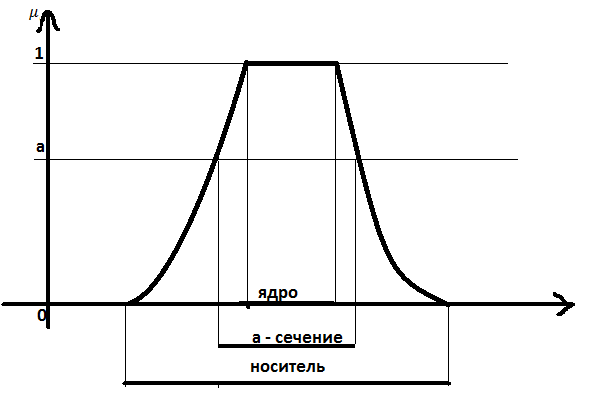
Носитель, ядро, а – сечение и а – уровень

Операции над нечёткими множествами

А и В множества с функциями принадлежност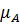и и 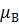соответственно.

А содержится в В, если

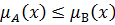
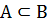
А и В равны тогда и только тогда, когда

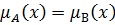
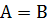
Пусть множество принадлежостей М=[0,1] (и будем полагать так в дальнейшем).

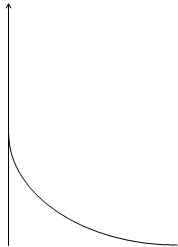
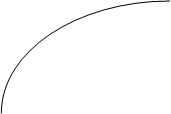
Множества А и В дополняют друг друга, если

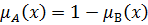
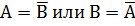
1

Множество

Дополнение

0 х

Нечёткое множество и его дополнение

Пересечение 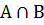определится как наибольшее нечёткое множество, содержащееся одновременно и в А и в В:

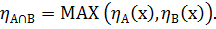
Пересечение множества и его дополнения не обязательно пусто.

1

В А

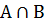
х

Пересечение двух нечётких множеств

Объединение 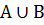– наименьшее нечёткое множество, содержащее как А, так и В:

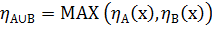
1

В А

Объединение двух нечётких множеств

Дефаззификацией называется процедура преобразования нечёткого множества в чёткое число.

Примеры дефаззификации:

Метод центра тяжести:

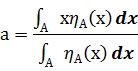
Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности множества.

Метод медианы:

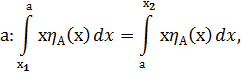
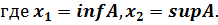
Геометрической интерпретацией метода медианы является нахождение такой точки на оси абсцисс, что перпендикуляр, восстановленный в этой точке, делит площадь под кривой функции принадлежности на две равные части.